基于图注意力神经网络的多智能体博弈抽象
G2ANet
《Multi-Agent Game Abstraction via Graph Attention Neural Network》
关键词:大规模,博弈抽象,2级(硬+软皆有)注意力机制,图神经网络
通过简化策略学习过程解决了大规模智能体的问题。
贡献
1.用完全图来建模(构建)智能体之间的关系。因为大规模的智能体场景中不是每个智能体都相互作用的,我们需要确定关系(交互还是不交互?),就像足球后卫后卫不需要总是盯着对方守门员一样。(硬权重决定了智能体之间的关系)
2.提出基于2级(硬+软)注意力网络的博弈抽象机制,这可以表明两个智能体之间是否存在相互作用,以及相互作用的重要性。也是硬+软注意力机制所分别做的工作。
3.将这个检测机制集成到基于图神经网络的多智能体强化学习中,进行博弈抽象。
4.将G2Net分别与一个策略网络和一个Q网络结合,以此提出了两种新的学习算法GA-Comm(基于通信)和GA-AC(基于AC)。
背景
博弈抽象的主要思想是将多智能体强化学习(马尔可夫博弈)的问题模型简化为一个较小的博弈,从而降低求解(或学习)博弈均衡策略的复杂性。
注意力机制
两个主要类型:软注意力(就理解为soft max 的吧!),硬注意力
软注意力计算元素的重要性分布。特别是软注意力机制是完全可微的,因此可以很容易地通过端到端的反向传播来训练。Softmax函数是一种常见的激活函数。然而,这个函数通常将非零概率分配给不相关的元素,这削弱了对真正重要元素的关注。
硬注意力从输入元素中选择一个子集,这迫使模型只关注重要元素,完全丢弃其他元素。然而,硬软注意力机制是选择基于抽样的元素,因此是不可微的。因此,它不能直接通过端到端的反向传播来学习注意力的权重。
方法
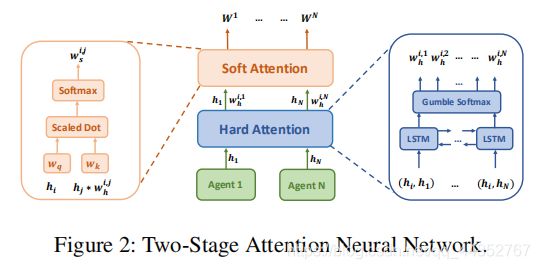
1.基于二级注意力机制的博弈抽象
提出基于2级注意力机制的博弈抽象方法。再基于此机制,提出GA-Comm和GA-AC算法。
考虑一个局部可观测环境。局部观测 o i t o^t_i oit被MLP编码成特征向量 h i t h^t_i hit。 然后,利用特征向量 h i t h^t_i hit通过注意力机制来学习智能体之间的关系(说的直接一点就是硬权重)。
首先用硬注意力机制来学习能够确定智能体之间是否有交互关系的硬权重。这篇论文是用LSTM来实现的,在每个时间步输出智能体i,j的的权重(0或者1)。 对于第i个智能体,将智能体i,j的嵌入向量合并为一个特征 ( h i , h j ) (h_i,h_j) (hi,hj),并将该特征输入进LSTM模型:
h i , j = f ( L S T M ( h i , h j ) ) (1) h_{i,j} = f(LSTM(h_i, h_j))\tag{1} hi,j=f(LSTM(hi,hj))(1)
其中 f f f是一个全连接层用来嵌入(解码)的。然而,传统的LSTM网络的输出只依赖于当前时间和前一时间的输入,而忽略了后期时间的输入信息。 也就是说,输入(智能体)的顺序在这个过程中扮演了重要角色并且输出重量值不能利用所有智能体的信息。这是短视且不合理的。所以用到了Bi-LSTM模型来解决此问题。
此外,在背景部分交代过,硬注意力机制因为采样过程,不能反向传播梯度。所以尝试利用gumbel-softmax函数来解决。
W h i , j = g u m ( f ( L S T M ( h i , h j ) ) ) (2) W^{i,j}_h = gum(f(LSTM(h_i, h_j)))\tag{2} Whi,j=gum(f(LSTM(hi,hj)))(2)
通过硬注意力机制,我们可以得到第i个智能体的子图 G i G_i Gi,在这个子图中第i个智能体刚好和需要协调的智能体连接。
然后,使用软注意力机制来学习子图 G i G_i Gi每条边的权重。使用查询键系统(键-值对),软注意力权重 W s i , j W^{i,j}_s Wsi,j将嵌入 e j e_j ej与 e i e_i ei进行比较,并将这两个嵌入之间的匹配值传递到softmax函数中:
W s i , j ∝ e x p ( e j T W k T W q e i W h i , j ) (3) W^{i,j}_s ∝ exp(e^T_j W^T_k W_qe_iW^{i,j}_h)\tag{3} Wsi,j∝exp(ejTWkTWqeiWhi,j)(3)
其中 W k W_k Wk将 e j e_j ej转换为一个密钥, W q W_q Wq将 e i e_i ei转换为一个查询, W h i , j W^{i,j}_h Whi,j是硬注意力值。最后,软注意力权重值 W s i , j W^{i,j}_s Wsi,j是边的最终权重,被定义为 W i , j W^{i,j} Wi,j。
2.基于博弈抽象的学习算法
通过两个阶段的注意力模型,我们可以得到一个约简图,其中每个智能体(节点)只连接到需要交互的智能体(节点)。
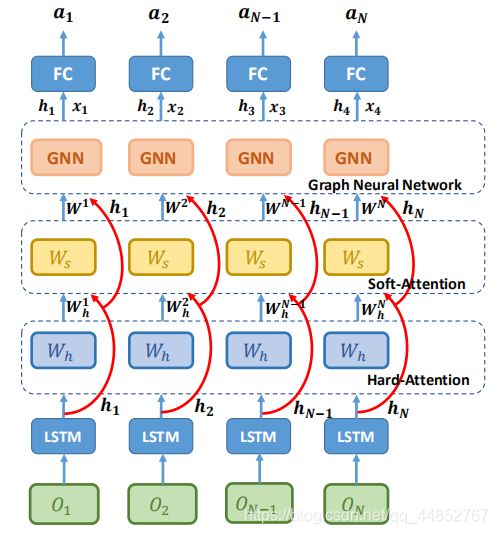
2.1基于博弈抽象的策略网络 GA-Comm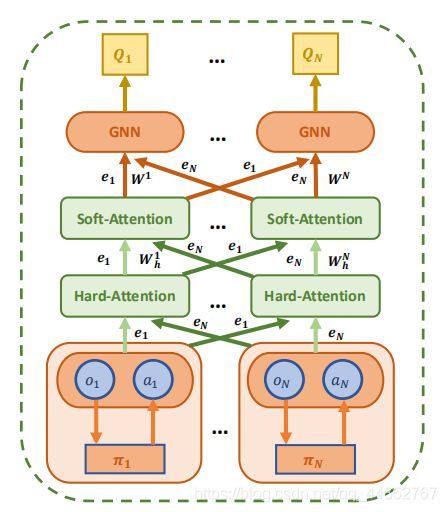
a i = π ( h i , x i ) a_i = π(h_i, x_i) ai=π(hi,xi)
上式为第i个智能体的策略 π \pi π,其中 h i , x i h_i,x_i hi,xi分别表示智能体的观测特征和其他智能体对第i个智能体的贡献。下面开始通过一系列方法得到 h i , x i h_i,x_i hi,xi,最后来求得策略 π \pi π。
用一个LSTM层来提取特征, e e e表示一个由全连接NN参数化的编码函数。 h i , s i h_i,s_i hi,si是LSTM的隐藏和cell状态。
h i , s i = L S T M ( e ( o i ) , h i , , s i , ) h_i, s_i= LSTM(e(o_i), h_i^,, s_i^,) hi,si=LSTM(e(oi),hi,,si,)
至于其他智能体对第i个智能体的贡献 x i x_i xi怎么得到呢?首先要使用2级注意力机制来选择哪个智能体是第i个智能体需要通信的并且获得它的重要性:
W h i , j = M h a r d ( h i , h j ) , W s i , j = M s o f t ( W h , h i , h j ) W^{i,j}_h = M_{hard}(h_i, h_j ), W^{i,j}_s = M_{soft}(W_h, h_i, h_j) Whi,j=Mhard(hi,hj),Wsi,j=Msoft(Wh,hi,hj)
其中 W h i , j W^{i,j}_h Whi,j表示硬注意力权重值,$ W^{i,j}s 是 软 注 意 力 值 , 这 两 者 都 由 是软注意力值,这两者都由 是软注意力值,这两者都由h_i, h_j 计 算 得 到 , 后 者 还 需 要 一 个 计算得到,后者还需要一个 计算得到,后者还需要一个W_h 。 同 理 , 。同理, 。同理,M{hard} 是 硬 注 意 力 模 型 , 是硬注意力模型, 是硬注意力模型,M_{soft}$是软注意力模型。
现在万事俱备,我们通过GNN来计算得到其他智能体对第i个智能体的贡献 x i x_i xi,具体计算方法如下:
x i = ∑ j ≠ x w j h j = ∑ j ≠ x W h i , j , W s i , j , h j x_i = \sum _{j\neq x} w_jh_j = \sum _{j\neq x} W_h^{i,j},W_s^{i,j},h_j xi=j=x∑wjhj=j=x∑Whi,j,Wsi,j,hj
最后,我们通过 a i = π ( h i , x i ) a_i = π(h_i, x_i) ai=π(hi,xi)得到了第i个智能体的动作。在训练过程中,用的是经典REINFORCE算法来训练策略 π \pi π。
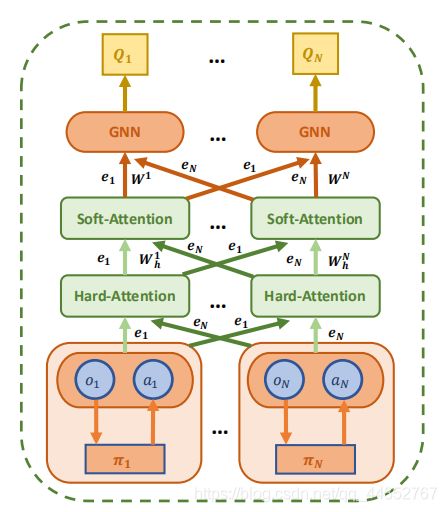
2.2基于博弈抽象的演员评论家网络 GA-AC
受到MAAC[Actor-Attention-Critic for Multi-Agent Reinforcement Learning]的启发,现在提出一个基于G2ANet的新算法。为了计算第i个智能体的Q值 Q i ( o i , a i ) Q_i(o_i,a_i) Qi(oi,ai),评论家网络接收所有智能体的观测值 o = ( o 1 , . . . , o N ) o=(o_1,...,o_N) o=(o1,...,oN)和动作 a = ( a 1 , . . . , a N ) a=(a_1,...,a_N) a=(a1,...,aN):
Q i ( o i , a i ) = f i ( g i ( o i , a i ) , x i ) Q_i(o_i, a_i) = f_i(g_i(o_i, a_i), x_i) Qi(oi,ai)=fi(gi(oi,ai),xi)
其中 f I f_I fI和 g i g_i gi是一个多层感知机(MLP),其他智能体对第i个智能体的贡献 x i x_i xi依然是由GNN计算得到,方法如下:
x i = ∑ j ≠ x w j v j = ∑ j ≠ x w j h ( V g j ( o j , a j ) ) x_i = \sum _{j\neq x} w_jv_j = \sum _{j\neq x} w_jh(Vg_j(o_j,a_j)) xi=j=x∑wjvj=j=x∑wjh(Vgj(oj,aj))
这里的值 v j v_j vj是第j个智能体的嵌入,用一个嵌入函数编码,然后通过一个共享矩阵V变换得到。 h ( ) h() h()是一个元素上的非线性。
通过2级注意力机制计算注意权重 w j w_j wj,将嵌入 e j e_j ej与 e i = g i ( o i , a i ) e_i=g_i(o_i,a_i) ei=gi(oi,ai)进行比较,并将这两个嵌入之间的关系值传递到一个softmax函数中:
w j = W h i , j W s i , j ∝ e x p ( h ( B i L S T M j ( e i , e j ) ) e j T W k T W q e i ) w_j = W_h^{i,j}W_s^{i,j} ∝ exp(h(BiLSTM_j (e_i, e_j ))e^T_j W^T_k W_qe_i) wj=Whi,jWsi,j∝exp(h(BiLSTMj(ei,ej))ejTWkTWqei)
其中 W q W_q Wq将 e i e_i ei转换为一个查询, W k W_k Wk将 e j e_j ej转换为一个密钥。 这样,我们就可以得到注意力权重 w j w_ j wj,并计算出每个智能体的Q值。