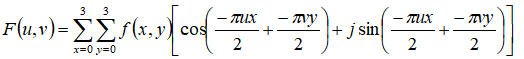二维离散傅里叶变换——数字图像处理学习六（C++版）
一、名词解释
FT(Fourier Transform),傅里叶变换
傅立叶变换，表示能将满足一定条件的某个函数表示成三角函数或者它们的积分的线性组合。在不同的研究领域，傅立叶变换具有多种不同的变体形式，如连续傅立叶变换和离散傅立叶变换。
1)傅里叶变换
![\large F\left ( \omega \right )= F\left [ f\left ( t \right ) \right ]= \int_{-\infty }^{+\infty }f\left ( t \right )e^{-i\omega t}dt](http://img.e-com-net.com/image/info8/f4af6c6d2c0746a7820ac94aac55080d.gif)
2)傅里叶逆变换
![\large f\left (t \right )= F^{-1}\left [ F\left ( \omega \right ) \right ]=\frac{1}{2\pi } \int_{-\infty }^{+\infty }F\left (\omega \right )e^{i\omega t}d\omega](http://img.e-com-net.com/image/info8/29ea749688bb457e99ceb729c86f2306.gif)
DFT(Discrete Fourier Transform),离散傅里叶变换
1)二维离散傅里叶变换
2)二维离散傅里叶拟变换
FFT(fast Fourier transform),快速傅里叶变换
快速傅里叶变换是计算机计算离散傅里叶变换的高效、快速的计算方法。采用这种算法能使计算机计算离散傅里叶变换需要的时间复杂度减少。
参考资料视频：https://www.bilibili.com/video/BV1za411F76U?from=search&seid=15738765176302809882
二、二维离散傅里叶变换的计算过程
例题：
解：根据二维离散傅里叶计算公式
其中M=4,N=4
和欧拉公式
可得：
其中
则当
时
为了加快计算，利用代码进行计算
#define PI 3.1415926
int main()
{
long double f[16] = { 1.0,7.0,8.0,9.0,5.0,2.0,6.0,7.0,3.0,4.0,7.0,8.0,2.0,1.0,4.0,7.0 };
long double dft2_data_real[16] = { 0 };
long double dft2_data_xu[16] = { 0 };
long double fixed_factor_for_axisX = (-2 * PI) / 4;//-2π/M
long double fixed_factor_for_axisY = (-2 * PI) / 4;//-2π/N
for (int u = 0; u < 4; u++)
{
for (int v = 0; v < 4; v++)
{
for (int x = 0; x < 4; x++)
{
for (int y = 0; y < 4; y++)
{
long double powerX = u * x * fixed_factor_for_axisX; //-2πux/M
long double powerY = v * y * fixed_factor_for_axisY; //-2πvy/N
long double real = f[y + x * 4] * cos(powerX + powerY);
long double xu = f[y + x * 4] * sin(powerX + powerY);
dft2_data_real[u * 4 + v] = dft2_data_real[u * 4 + v]+real;
dft2_data_xu[u * 4 + v] = dft2_data_xu[u * 4 + v]+xu;
}
}
}
}
for (int u = 0; u < 4; u++)
{
for (int v = 0; v < 4; v++)
{
cout << "real:" << dft2_data_real[u * 4 + v] << "xu:" << dft2_data_xu[u * 4 + v] << endl;
}
}
}执行结果
所以结果为
三、图像的离散傅里叶变换
原灰度图：
展示频谱图
void dft()
{
CPaintDC dc(this);
FILE* fp1;
if (fopen_s(&fp1, "C:\\Users\\Administrator\\Desktop\\BMP1\\BMP1\\1.bmp", "rb") != 0) {
return;
}
bmpFileHeader bfHead1;
bmpInfoHeader biHead1;
fread_s(&bfHead1, 14, 14, 1, fp1);
fread_s(&biHead1, 40, 40, 1, fp1);
uchar* p1 = (uchar*)malloc(biHead1.biSizeImage * sizeof(uchar));
fseek(fp1, bfHead1.bfOffBits, SEEK_SET);
fread_s(p1, biHead1.biSizeImage * sizeof(uchar), biHead1.biSizeImage * sizeof(uchar), 1, fp1);
///灰度化
unsigned long x = 0;
uchar* gray = (uchar*)malloc(biHead1.biHeight * biHead1.biWidth * sizeof(uchar));
for (int i = 0; i < biHead1.biHeight; i++)
{
for (int j = 0; j < biHead1.biWidth; j++)
{
gray[i * biHead1.biWidth + j] = 0.2989 * p1[x + 2] + 0.5870 * p1[x + 1] + 0.1140 * p1[x];
x += 3;
}
}
//转成double型
double* double_data = new double[biHead1.biHeight * biHead1.biWidth];
for (int i = 0; i < biHead1.biHeight; i++)
for (int j = 0; j < biHead1.biWidth; j++)
{
double_data[i * biHead1.biWidth + j] = (double)gray[i * biHead1.biWidth + j];
}
// 对 double_data 进行傅里叶变换
double* dft2_data_real = new double[biHead1.biHeight * biHead1.biWidth]();//初始化0
double* dft2_data_xu = new double[biHead1.biHeight * biHead1.biWidth]();//初始化0
double fixed_factor_for_axisX = (-2 * PI) / biHead1.biHeight;//-2π/M
double fixed_factor_for_axisY = (-2 * PI) / biHead1.biWidth;//-2π/N
for (int u = 0; u < biHead1.biHeight; u++)
{
for (int v = 0; v < biHead1.biWidth; v++)
{
for (int x = 0; x < biHead1.biHeight; x++)
{
for (int y = 0; y < biHead1.biWidth; y++)
{
double powerX = u * x * fixed_factor_for_axisX; //-2πux/M
double powerY = v * y * fixed_factor_for_axisY; //-2πvy/N
double real = double_data[y + x * biHead1.biWidth] * cos(powerX + powerY);
double xu = double_data[y + x * biHead1.biWidth] * sin(powerX + powerY);
dft2_data_real[u * biHead1.biWidth + v] = dft2_data_real[u * biHead1.biWidth + v] + real;
dft2_data_xu[u * biHead1.biWidth + v] = dft2_data_xu[u * biHead1.biWidth + v] + xu;
}
}
}
}
// 将傅里叶数组归一化
// 取模
double* mold = new double[biHead1.biHeight * biHead1.biWidth];
for (int i = 0; i < biHead1.biHeight * biHead1.biWidth; i++)
{
mold[i] = sqrt(dft2_data_real[i] * dft2_data_real[i] + dft2_data_xu[i] * dft2_data_xu[i]);
}
// 获取最小值
double min = mold[0];
for (int i = 0; i < biHead1.biHeight * biHead1.biWidth; i++)
{
if (mold[i] < min)
min = mold[i];
}
// 获取去掉前几大值的最大值
double maxqueue[20] = { 0.,0.,0.,0.,0.,0.,0.,0.,0.,0.,0.,0.,0.,0.,0.,0.,0.,0.,0.,0. }, max;
for (int i = 0; i < biHead1.biHeight * biHead1.biWidth; i++)
{
if (mold[i] > maxqueue[0])
maxqueue[0] = mold[i];
}
for (int j = 1; j < 20; j++)
{
for (int i = 0; i < biHead1.biHeight * biHead1.biWidth; i++)
{
if (mold[i] > maxqueue[j] && mold[i] < maxqueue[j - 1])
maxqueue[j] = mold[i];
}
}
max = maxqueue[19];
unsigned char* normalized_data = new unsigned char[biHead1.biHeight * biHead1.biWidth];
for (int i = 0; i < biHead1.biHeight; i++)
for (int j = 0; j < biHead1.biWidth; j++)
{
unsigned char t = (unsigned char)((mold[i * biHead1.biWidth + j] - min) / (max - min) * 255);
if (t > 255)
t = 255;
normalized_data[i * biHead1.biWidth + j] = t;
}
// 将图像中心化
unsigned char* center_data = new unsigned char[biHead1.biHeight * biHead1.biWidth];
for (int u = 0; u < biHead1.biHeight; u++)
{
for (int v = 0; v < biHead1.biWidth; v++)
{
if ((u < (biHead1.biHeight/ 2)) && (v < (biHead1.biWidth / 2)))
center_data[v + u * biHead1.biWidth] =normalized_data[biHead1.biWidth / 2 + v + (biHead1.biHeight / 2 + u) * biHead1.biWidth];
else if ((u < (biHead1.biHeight / 2)) && (v >= (biHead1.biWidth / 2)))
center_data[v + u * biHead1.biWidth] =normalized_data[(v - biHead1.biWidth / 2) + (biHead1.biHeight / 2 + u) * biHead1.biWidth];
else if ((u >= (biHead1.biHeight / 2)) && (v < (biHead1.biWidth / 2)))
center_data[v + u * biHead1.biWidth] =normalized_data[(biHead1.biWidth / 2 + v) + (u - biHead1.biHeight / 2) * biHead1.biWidth];
else if ((u >= (biHead1.biHeight / 2)) && (v >= (biHead1.biWidth / 2)))
center_data[v + u * biHead1.biWidth] =normalized_data[(v - biHead1.biWidth / 2) + (u - biHead1.biHeight / 2) * biHead1.biWidth];
}
}
// 向中心化的数组填充空间，频谱图显示
int bytesPerLine = (biHead1.biWidth * 8 + 31) / 32 * 4;
unsigned char* dst_data = new unsigned char[bytesPerLine * biHead1.biHeight];
for (int i = 0; i < biHead1.biHeight; i++)
for (int j = 0; j < biHead1.biWidth; j++)
{
dst_data[i * bytesPerLine + j] = center_data[i * biHead1.biWidth + j];
dc.SetPixel(j/time, (biHead1.biHeight - i)/time, RGB(dst_data[j + i * biHead1.biWidth], dst_data[j + i * biHead1.biWidth], dst_data[j + i * biHead1.biWidth]));
}
}频谱图显示结果：
离散傅里叶逆变换：
void ni()
{
CPaintDC dc(this);
FILE* fp1;
if (fopen_s(&fp1, "C:\\Users\\Administrator\\Desktop\\BMP1\\BMP1\\1.bmp", "rb") != 0) {
return;
}
bmpFileHeader bfHead1;
bmpInfoHeader biHead1;
fread_s(&bfHead1, 14, 14, 1, fp1);
fread_s(&biHead1, 40, 40, 1, fp1);
uchar* p1 = (uchar*)malloc(biHead1.biSizeImage * sizeof(uchar));
fseek(fp1, bfHead1.bfOffBits, SEEK_SET);
fread_s(p1, biHead1.biSizeImage * sizeof(uchar), biHead1.biSizeImage * sizeof(uchar), 1, fp1);
///灰度化
unsigned long x = 0;
uchar* gray = (uchar*)malloc(biHead1.biHeight * biHead1.biWidth * sizeof(uchar));
for (int i = 0; i < biHead1.biHeight; i++)
{
for (int j = 0; j < biHead1.biWidth; j++)
{
gray[i * biHead1.biWidth + j] = 0.2989 * p1[x + 2] + 0.5870 * p1[x + 1] + 0.1140 * p1[x];
x += 3;
}
}
//转成double型
double* double_data = new double[biHead1.biHeight * biHead1.biWidth];
for (int i = 0; i < biHead1.biHeight; i++)
for (int j = 0; j < biHead1.biWidth; j++)
{
double_data[i * biHead1.biWidth + j] = (double)gray[i * biHead1.biWidth + j];
}
// 对 double_data 进行傅里叶变换
double* dft2_data_real = new double[biHead1.biHeight * biHead1.biWidth]();//初始化0
double* dft2_data_xu = new double[biHead1.biHeight * biHead1.biWidth]();//初始化0
double fixed_factor_for_axisX = (-2 * PI) / biHead1.biHeight;//-2π/M
double fixed_factor_for_axisY = (-2 * PI) / biHead1.biWidth;//-2π/N
for (int u = 0; u < biHead1.biHeight; u++)
{
for (int v = 0; v < biHead1.biWidth; v++)
{
for (int x = 0; x < biHead1.biHeight; x++)
{
for (int y = 0; y < biHead1.biWidth; y++)
{
double powerX = u * x * fixed_factor_for_axisX; //-2πux/M
double powerY = v * y * fixed_factor_for_axisY; //-2πvy/N
double real = double_data[y + x * biHead1.biWidth] * cos(powerX + powerY);
double xu = double_data[y + x * biHead1.biWidth] * sin(powerX + powerY);
dft2_data_real[u * biHead1.biWidth + v] = dft2_data_real[u * biHead1.biWidth + v] + real;
dft2_data_xu[u * biHead1.biWidth + v] = dft2_data_xu[u * biHead1.biWidth + v] + xu;
}
}
}
}
//逆傅里叶变换
//double* double_data = new double[biHead1.biHeight * biHead1.biWidth];
fixed_factor_for_axisX = (2 * PI) / biHead1.biHeight;//2π/M
fixed_factor_for_axisY = (2 * PI) / biHead1.biWidth;//2π/N
double_data[0] = 0;
for (int x = 0; x < biHead1.biHeight; x++)
{
for (int y = 0; y < biHead1.biWidth; y++)
{
for (int u = 0; u < biHead1.biHeight; u++)
{
for (int v = 0; v < biHead1.biWidth; v++)
{
double powerX = u * x * fixed_factor_for_axisX; //2πux/M
double powerY = v * y * fixed_factor_for_axisY; //2πvy/N
double real = dft2_data_real[v + u * biHead1.biWidth] * cos(powerX + powerY) - dft2_data_xu[v + u * biHead1.biWidth] * sin(powerX + powerY);
double_data[x * biHead1.biWidth + y] = double_data[x * biHead1.biWidth + y] + real;
}
}
double_data[x * biHead1.biWidth + y] = double_data[x * biHead1.biWidth + y] / (biHead1.biHeight * biHead1.biWidth);
}
}
//逆傅里叶变换图片显示
for (int i = 0; i < biHead1.biHeight; i++)
for (int j = 0; j < biHead1.biWidth; j++)
{
dc.SetPixel(j / time, (biHead1.biHeight - i) / time, RGB(double_data[j + i * biHead1.biWidth], double_data[j + i * biHead1.biWidth], double_data[j + i * biHead1.biWidth]));
}
}逆变换结果：
注意：本文处理图像时未利用FFT方法，在实际应用中，处理M*N像素的图片DFT方法时间复杂度为M*N*M*N，FFT作者还未清楚，待日后学习补充