【Python】机器学习笔记01：scikit-learn简介

机器学习

机器学习可以分为有监督的学习和无监督的学习，有监督的学习指的是在数据的若干特征和对应的标签之间的关系，根据标签是离散值还是连续值，有监督的学习可以进一步被分为分类任务与回归任务；
无监督的学习是对不带任何标签的数据进行建模，是一种“让数据自己介绍自己”的过程，无监督的学习可以被进一步分为聚类与降维任务，聚类算法可以自动将数据分为不同的组别，降维算法可以让我们用更少的特征来表示数据；

如果要使用Python进行机器学习，最常用的包是scikit-learn，这个包中集成了许多经典的机器学习算法和常用数据集，适合初学者接触机器学习；

本文的内容参考《Python数据科学手册》；

包导入

%matplotlib inline
import pandas as pd
import seaborn as sns
from matplotlib.pylab import *

from sklearn.linear_model import LinearRegression
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, confusion_matrix
from sklearn.decomposition import PCA
from sklearn.mixture import GaussianMixture
from sklearn.manifold import Isomap
from sklearn.datasets import load_digits

sns.set()
plt.rc('font', family='SimHei')
plt.rc('axes', unicode_minus=False)

有监督的学习示例：线性回归

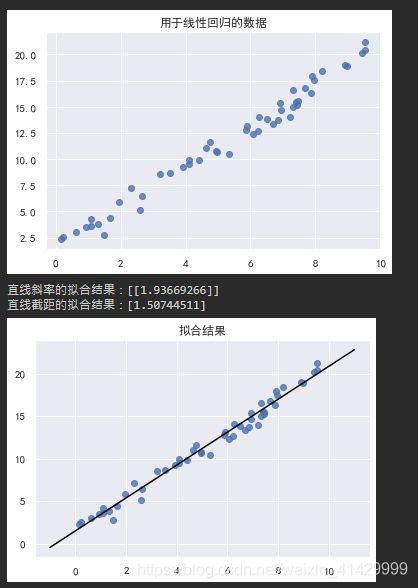
我们构造一组线性的随机数据，然后使用scikit-learn中的LinearRegression类来进行线性回归任务，拟合直线；

x = np.random.rand(50) * 10  # rand是0-1之间的平均分布
y = 2 * x + 1 + np.random.randn(50)
x = x[:, np.newaxis]
y = y[:, np.newaxis]

plt.scatter(x, y, alpha=0.8)
plt.title('用于线性回归的数据')
plt.show()

linear_model = LinearRegression(fit_intercept=True)
linear_model.fit(x, y)
print(f'直线斜率的拟合结果：{linear_model.coef_}')  # 使用fit而计算得到的参数在sklearn中都会带有下划线
print(f'直线截距的拟合结果：{linear_model.intercept_}')

x_fit = linspace(-1, 11, 50)[:, np.newaxis]
y_fit = linear_model.predict(x_fit)
plt.scatter(x, y, alpha=0.8)
plt.plot(x_fit, y_fit, color='black')
plt.title('拟合结果')
plt.show()

有监督的学习示例：鸢尾花数据分类

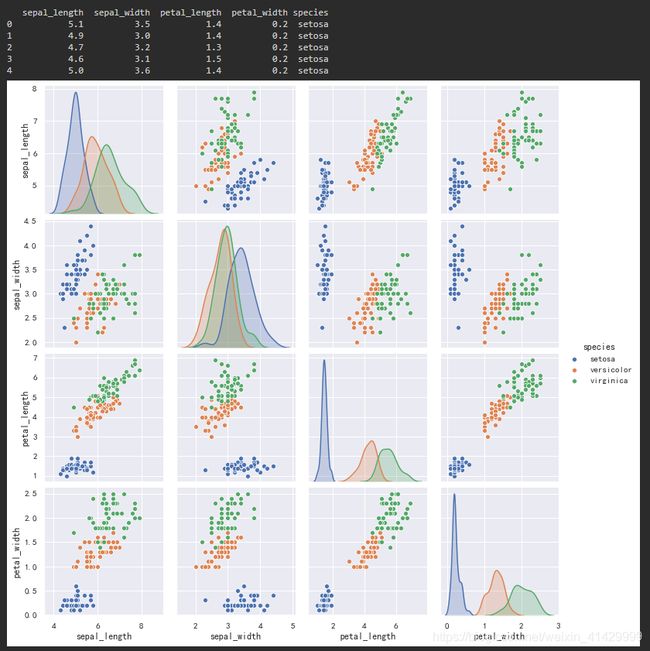
这里使用Seaborn包提供的鸢尾花数据，将数据通过pandas的read_csv方法转化为DataFrame对象，并使用Seaborn的pairplot方法绘制矩阵图：

iris = pd.read_csv('./seaborn_dataset/iris.csv')
print(iris.head())
sns.pairplot(data=iris, hue='species')
plt.show()

接下来使用scikit-learn提供的高斯朴素贝叶斯分类器对鸢尾花数据进行分类；
在训练模型之前，先使用train_test_split函数分割数据集，将数据集分割为训练集与测试集；
训练模型，使用GaussianNB类的fit方法，用训练好的模型预测未知数据，使用GaussianNB类的predict方法；
最后使用accuracy_score函数计算模型的准确度；
accuracy+score、train_test_split、GaussianNB均由scikit-learn包提供；

iris_x = iris.drop('species', axis=1)
iris_y = iris['species']

iris_train_x, iris_test_x, iris_train_y, iris_test_y  =train_test_split(iris_x, iris_y, random_state=1)
nb_model = GaussianNB()
nb_model.fit(iris_train_x, iris_train_y)

iris_model_res = nb_model.predict(iris_test_x)
print(f'高斯朴素贝叶斯的准确度为：{accuracy_score(iris_test_y, iris_model_res) * 100:.3f}%')

我最后得到的模型准确率是97.368%；

无监督的学习示例：鸢尾花数据降维

这里，我们使用主成分分析（Principle Component Analysis）对鸢尾花数据进行降维操作；
鸢尾花数据集原始数据是4维的，这里我们将其降维二维并绘制散点图（这里参照书本使用seaborn绘图）；
主成分分析使用scikit-learn提供的PCA类实现；

pca_model = PCA(n_components=2)  # 将数据降成二维
pca_model.fit(iris_x)

iris_2d = pca_model.transform(iris_x)
iris['PCA1'] = iris_2d[:, 0]
iris['PCA2'] = iris_2d[:, 1]

sns.lmplot('PCA1', 'PCA2', hue='species', data=iris, fit_reg=False)
plt.show()

无监督的学习示例：鸢尾花数据聚类

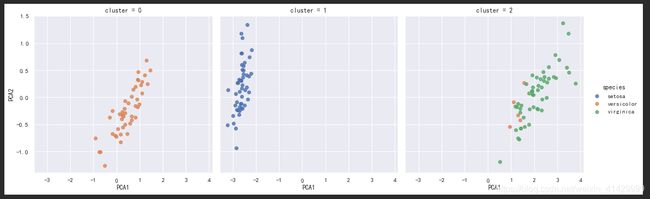
这里使用高斯混合模型对鸢尾花数据进行聚类，并借助上文降维得到的结果进行可视化；
可视化依旧使用Seaborn进行；

gmm_model = GaussianMixture(n_components=3, covariance_type='full')
gmm_model.fit(iris_x)
gmm_res = gmm_model.predict(iris_x)
iris['cluster'] = gmm_res
sns.lmplot('PCA1', 'PCA2', data=iris, hue='species', col='cluster', fit_reg=False)
plt.show()

可以看到，第一种与第三种鸢尾花的聚类结果存在一定误差；

案例：手写数字探索

这里使用scikit-learn提供的手写数字数据集，每一个数字是$8\times 8$分辨率的，这意味着原始数据是64维的；

加载并显示手写数字

首先，我们尝试加载并可视化手写数字数据集：
加载数据集，可以直接使用scikit-learn提供的load_digits函数，首次加载会从网络获取数据，数据集的实际文件会保存在YourPythonInterpreterLocation\Lib\site-packages\sklearn\datasets\data\xxx；
显示数字，可以使用matplotlib提供的imshow函数，并将颜色映射方案设置为binary；

digits = load_digits()
print(digits.images.shape)

fig, axs = plt.subplots(10, 10, figsize=(10, 10))
for i, ax in enumerate(axs.flat):
    ax.imshow(digits.images[i], cmap='binary')
    ax.set_xticks([])
    ax.set_yticks([])
    ax.text(0.05, 0.05, f'{digits.target[i]}', color='green')

digits_x = digits.data
print(digits_x.shape)
digits_y = digits.target
print(digits_y.shape)

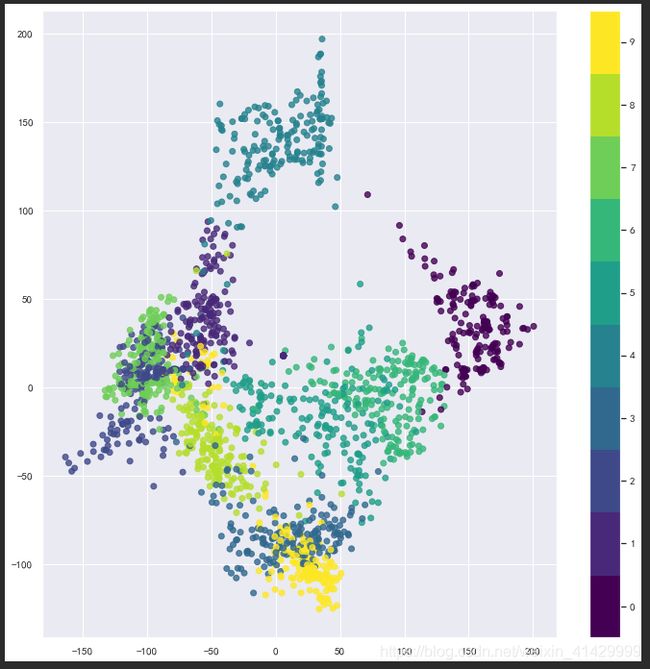
手写数字降维

这里使用scikit-learn提供的Isomap类进行降维，将64维的数据降维至2维：

ios_model = Isomap(n_components=2)
ios_model.fit(digits_x)
digits_ios_res = ios_model.transform(digits_x)

fig, ax = plt.figure(figsize=(12, 12)), plt.axes()
ax.scatter(x=digits_ios_res[:, 0], y=digits_ios_res[:, 1], c=digits_y, alpha=0.8, cmap=plt.cm.get_cmap('viridis', 10))
mappable = plt.cm.ScalarMappable(cmap=plt.cm.get_cmap('viridis', 10))
mappable.set_clim(-0.5, 9.5)
fig.colorbar(mappable, ticks=range(10))

手写数字分类

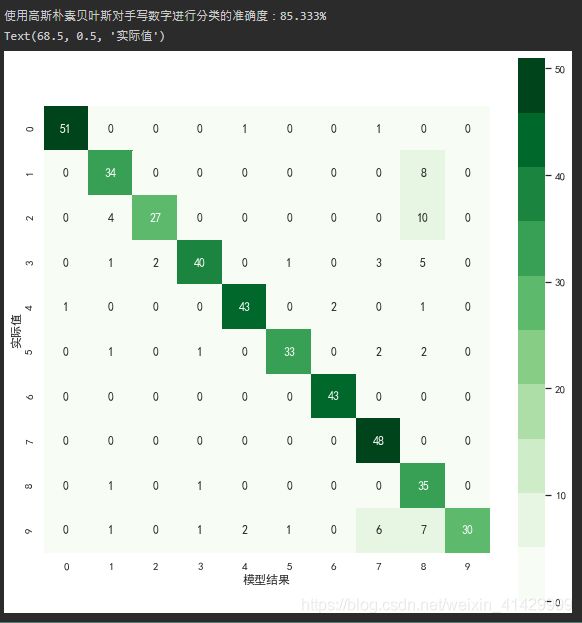
这里我们使用高斯朴素贝叶斯分类器对64维的原始数据直接进行分类，并使用scikit-learn提供的confusion_matrix函数计算混淆矩阵以查看模型效果，混淆矩阵的可视化使用Seaborn的heatmap函数；

digits_train_x, digits_test_x, digits_train_y, digits_test_y = train_test_split(digits_x, digits_y, random_state=1)
nb_model = GaussianNB()
nb_model.fit(digits_train_x, digits_train_y)
digits_nb_res = nb_model.predict(digits_test_x)

print(f'使用高斯朴素贝叶斯对手写数字进行分类的准确度：{accuracy_score(digits_test_y, digits_nb_res)*100:.3f}%')

cf_mat = confusion_matrix(digits_test_y, digits_nb_res)
plt.figure(figsize=(10, 10))
sns.heatmap(data=cf_mat, square=True, annot=True, cbar=True, cmap=plt.cm.get_cmap('Greens', 10))
plt.xlabel('模型结果')
plt.ylabel('实际值')

可以看到，一个简单的贝叶斯模型就可以让手写数字分类的准确率达到85%，通过查看混淆矩阵的结果，我们可以看到模型的错误主要集中在哪里；

完整代码（Jupyter Notebook）

#%%

%matplotlib inline
import pandas as pd
import seaborn as sns
from matplotlib.pylab import *

from sklearn.linear_model import LinearRegression
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, confusion_matrix
from sklearn.decomposition import PCA
from sklearn.mixture import GaussianMixture
from sklearn.manifold import Isomap
from sklearn.datasets import load_digits

sns.set()
plt.rc('font', family='SimHei')
plt.rc('axes', unicode_minus=False)

#%% md

# 有监督的学习示例：简单线性回归

#%%

x = np.random.rand(50) * 10  # rand是0-1之间的平均分布
y = 2 * x + 1 + np.random.randn(50)
x = x[:, np.newaxis]
y = y[:, np.newaxis]

plt.scatter(x, y, alpha=0.8)
plt.title('用于线性回归的数据')
plt.show()

linear_model = LinearRegression(fit_intercept=True)
linear_model.fit(x, y)
print(f'直线斜率的拟合结果：{linear_model.coef_}')  # 使用fit而计算得到的参数在sklearn中都会带有下划线
print(f'直线截距的拟合结果：{linear_model.intercept_}')

x_fit = linspace(-1, 11, 50)[:, np.newaxis]
y_fit = linear_model.predict(x_fit)
plt.scatter(x, y, alpha=0.8)
plt.plot(x_fit, y_fit, color='black')
plt.title('拟合结果')
plt.show()

#%% md

# 有监督的学习示例：鸢尾花数据分类

#%%

iris = pd.read_csv('./seaborn_dataset/iris.csv')
print(iris.head())
sns.pairplot(data=iris, hue='species')
plt.show()

#%%

iris_x = iris.drop('species', axis=1)
iris_y = iris['species']

iris_train_x, iris_test_x, iris_train_y, iris_test_y  =train_test_split(iris_x, iris_y, random_state=1)
nb_model = GaussianNB()
nb_model.fit(iris_train_x, iris_train_y)

iris_model_res = nb_model.predict(iris_test_x)
print(f'高斯朴素贝叶斯的准确度为：{accuracy_score(iris_test_y, iris_model_res) * 100:.3f}%')

#%% md

# 无监督学习示例：鸢尾花数据降维

这里使用主成分分析

#%%

pca_model = PCA(n_components=2)  # 将数据降成二维
pca_model.fit(iris_x)

iris_2d = pca_model.transform(iris_x)
iris['PCA1'] = iris_2d[:, 0]
iris['PCA2'] = iris_2d[:, 1]

sns.lmplot('PCA1', 'PCA2', hue='species', data=iris, fit_reg=False)
plt.show()

#%% md

# 无监督学习示例：鸢尾花数据聚类

使用高斯混合模型

#%%

gmm_model = GaussianMixture(n_components=3, covariance_type='full')
gmm_model.fit(iris_x)
gmm_res = gmm_model.predict(iris_x)
iris['cluster'] = gmm_res
sns.lmplot('PCA1', 'PCA2', data=iris, hue='species', col='cluster', fit_reg=False)
plt.show()

#%% md

# 应用：手写数字分类

sklearn中的手写数字数据集是8×8像素的，意味着每个数字都有64个维度，所以我们使用isomap算法进行降维，然后对数据进行可视化；
之后使用高斯朴素贝叶斯对手写数字进行分类；
最后使用混淆矩阵查看

#%%

digits = load_digits()
print(digits.images.shape)

fig, axs = plt.subplots(10, 10, figsize=(10, 10))
for i, ax in enumerate(axs.flat):
    ax.imshow(digits.images[i], cmap='binary')
    ax.set_xticks([])
    ax.set_yticks([])
    ax.text(0.05, 0.05, f'{digits.target[i]}', color='green')

digits_x = digits.data
print(digits_x.shape)
digits_y = digits.target
print(digits_y.shape)

#%%

ios_model = Isomap(n_components=2)
ios_model.fit(digits_x)
digits_ios_res = ios_model.transform(digits_x)

fig, ax = plt.figure(figsize=(12, 12)), plt.axes()
ax.scatter(x=digits_ios_res[:, 0], y=digits_ios_res[:, 1], c=digits_y, alpha=0.8, cmap=plt.cm.get_cmap('viridis', 10))
mappable = plt.cm.ScalarMappable(cmap=plt.cm.get_cmap('viridis', 10))
mappable.set_clim(-0.5, 9.5)
fig.colorbar(mappable, ticks=range(10))

#%%

digits_train_x, digits_test_x, digits_train_y, digits_test_y = train_test_split(digits_x, digits_y, random_state=1)
nb_model = GaussianNB()
nb_model.fit(digits_train_x, digits_train_y)
digits_nb_res = nb_model.predict(digits_test_x)

print(f'使用高斯朴素贝叶斯对手写数字进行分类的准确度：{accuracy_score(digits_test_y, digits_nb_res)*100:.3f}%')

cf_mat = confusion_matrix(digits_test_y, digits_nb_res)
plt.figure(figsize=(10, 10))
sns.heatmap(data=cf_mat, square=True, annot=True, cbar=True, cmap=plt.cm.get_cmap('Greens', 10))
plt.xlabel('模型结果')
plt.ylabel('实际值')