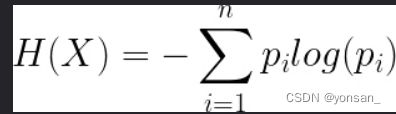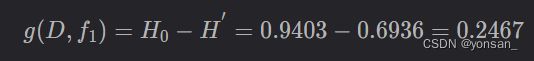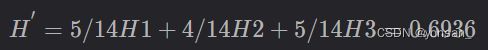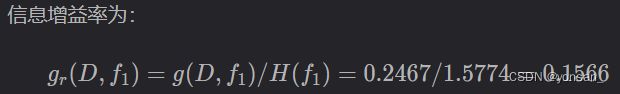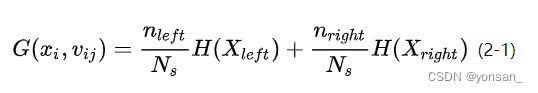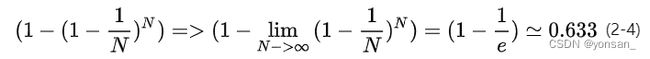决策树与随机森林

决策树与随机森林应该是MLer接触到最简单，最实用，最容易理解的ML算法。

那么，具体是怎么实现回归的呢？看了下面这篇博客，算是更加理解了数学原理。(16条消息) 决策树与随机森林(从入门到精通)_Cyril_KI的博客-CSDN博客_关于决策树与随机森林的描述正确的是zhttps://blog.csdn.net/Cyril_KI/article/details/107162316?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522165391120916781483799761%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=165391120916781483799761&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-2-107162316-null-null.142%5Ev11%5Epc_search_result_control_group,157%5Ev12%5Econtrol&utm_term=%E5%86%B3%E7%AD%96%E6%A0%91&spm=1018.2226.3001.4187

总结如下：

第一点：通信这门课的信息熵知识：

熵越小，不确定性越小，就是回归地更加准确。决策树就是不断减小熵值来达到回归的目的。

第二点：决策树模型：

决策树模型类似于二叉树的形状。

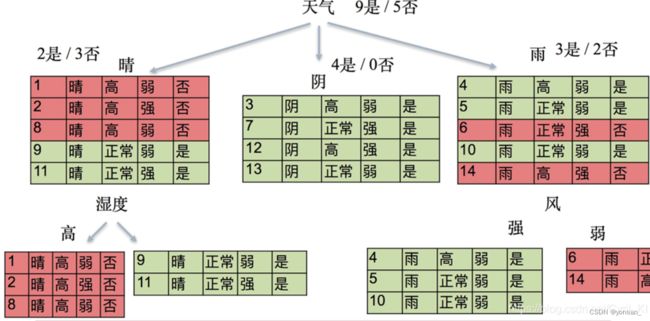
第三点：实例

 二叉树进行分层：第一层天气，第二层适度，第三层风

 第一层的熵值计算：

第二层的熵值计算：

 可以发现，熵值是下降的，那么如何选择熵值下降的方法呢？

 3.1 信息增益与ID3

在我选择了天气这一特征之后，信息熵下降为0.6936，信息熵下降了0.2467，也就是信息增益为0.2467.
 

 3.2 信息增益率

为了解决信息增益的局限，引入了信息增益率的概念。

第二层的熵是：

所以增加的信息是：

注意：要除以天气本身的熵。这是什么意思呢？我们计算的H'是 晴、阴、雨 对出不出去打球的熵（熵是不确定性）。这里求信息增率，我们需要求出 天气变化：晴、阴、雨 的不确定性。这个计算方式就是与贝叶斯公式类似。

贝叶斯公式： P(A|B)=P(B|A)*P(A)/P(B)。

 现在我们要利用信息增益率来决定谁做根节点。

总结：

决策树可以看做是由若干个点（根节点和其他节点）构成，根节点存放着所有的数据（整个数据集），然后从根节点开始，从数据集中选择属性，从属性中找出分裂规则（问题），根据属性中的问题，对于整个数据集进行分裂，然后不断的找出下一个属性，得到问题，再分裂，直到满足以下条件：

1. 树达到指定的最大深度（max_depth），每次分割视为一层。
2. 所有叶子节点中的样本属于同一个类别（不纯度最低）。
3. 所有叶子节点包含的样本数量小于指定的最小分类样本（min_samples_split）数量。

划分数据集（设置问题）的标准：

1. 将数据集中的每一个特征看成是一种划分可能。
    * 对于划分方式，可以分为离散型与连续性属性。
      * 离散型属性，每一个类别可以划分为属于类别A与不属于类别A（二叉树）。
      * 连续性属性，可以划分为大于等于A与小于A。
2. 从根节点开始，选择可获的(最大信息增益)的特征进行节点划分。
3. 划分的目的就是，可以在每次划分时，实现对信息增益的最大化

那么信息增率的计算方法如下：

IG是信息增率，Dp是当前节点，f是当前的问题，Np是当前节点的所有样本数量，Nj是第j个子节点的样本数量，Dj是第j个子节点，I（）是不纯度的计算方式，I（Dp）是当前节点不纯度，后面的式子是子节点的不纯度之和，二者相减之后就得到信息增率。

很多Python库的是二叉树如sklearn，所以计算方式也可以按照下图进行计算：

I（Dp）是确定的，不变的，所以要对子节点变得更小，得到更大的信息增率。

 子节点不纯度加权：

 

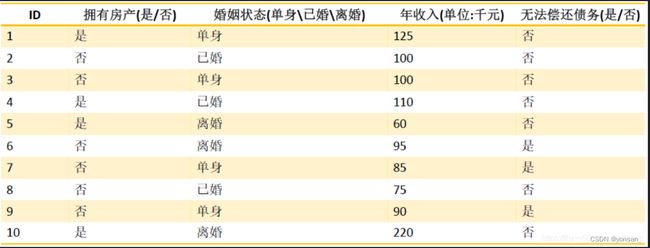
 例子：

 在计算中，对于本节点的I（Dp）的计算方式，就是该事件发生的概率，与后续的结果无关。

如果，该节点的属性是是否能偿还债务，那么I（Dp）=-1*（0.3*log0.3 + 0.7*log（0.7））

他划分子节点的问题是：是否有房产，那么就开始计算：

同理：计算婚姻

计算年收入：

 第四点 随机森林

随机森林也是为了解决决策树的过拟合问题。

3.1 Bootstrap

概括：训练多个弱模型打包起来组成一个强模型，其中的弱模型可以是决策树、SVM等模型，在随机森林中，弱模型选用决策树。bootstrap就是个采样手段，从输入训练数据集中采集多个不同的子训练数据集，来训练出不同的弱模型。（如果用一样的数据集，训练出的弱模型是一样的，那就没有意义了。）

详解：假设有一个大小为N的样本，我们希望从中得到m个大小为N的样本用来训练。bootstrap的思想是：首先，在个样本里随机抽出一个样本x1，然后记下来，放回去，再抽出一个x2，… ，这样重复N次，即可得到N个新样本，这个新样本里可能有重复的。重复m次，就得到了m个这样的样本。实际上就是一个有放回的随机抽样问题。每一个样本在每一次抽的时候有同样的概率（1/N）被抽中。所以在一次大采样过程中，每个样本被采集到的概率是0.633。

 

 

直观一点，就是生成多个样本。

3.2 bagging策略
bagging的名称来源于： Bootstrap Aggregating，意为自助抽样集成。既然出现了Bootstrap那么定就会使用到Bootstrap方法，其基本策略是：

在所有属性上，对每一个样本集建立分类器。
将数据放在这m个分类器上，最后根据m个分类器的投票结果，决定数据最终属于哪一类。如果是回归问题，就采用均值。
什么时候用bagging？当模型过于复杂容易产生过拟合时，才使用bagging，决策树就容易产生过拟合。

因此，可以直观感觉到：随机森林就是多个决策树的集合，在回归问题上，取均值计算。

3.3 out of bag estimate（包外估计）
在使用bootstrap来生成样本集时，由于我们是有放回抽样，那么可能有些样本会被抽到多次，而有的样本一次也抽不到。我们来做个计算：假设有N个样本，每个样本被抽中的概率都是1/N，没被选中的概率就是1-1/N，重复N次都没被选中的概率就是( 1 − 1 / N ) N (1-1/N)^N(1−1/N) 
N
 ，当N趋于无穷时，这个概率就是1/e，大概为36.8%。也就是说样本足够多的时候，一个样本没被选上的概率有36.8%，那么这些没被选中的数据可以留作验证集。每一次利用Bootstrap生成样本集时，其验证集都是不同的。

以这些没被选中的样本作为验证集的方法称为包外估计。

3.4 样本随机与特征随机
在我们使用Bootstrap生成m个样本集时，每一个样本集的样本数目不一定要等于原始样本集的样本数目，比如我们可以生成一个含有0.75N个样本的样本集，此处0.75就称为采样率。

样本随机——就是前文所说的bagging策略，生成多个随机样本。

特征随机——随机选择特征生成决策树，生成多个随机决策树。

同样，我们在利用0.75N个样本生成决策树时，假设我们采用ID3算法，生成结点时以信息增益作为判断依据。我们的具体做法是把每一个特征都拿来试一试，最终信息增益最大的特征就是我们要选的特征。但是，我们在选择特征的过程中，也可以只选择一部分特征，比如20个里面我只选择16个特征。
那可能有的人就要问了，假设你没选的4个特征里面刚好有一个是最好的呢？这种情况是完全可能出现的，但是我们在下一次的分叉过程中，该特征是有可能被重新捡回来的，另外别的决策树当中也可能会出现那些在另一颗决策树中没有用到的特征。

随机森林的定义就出来了，利用bagging策略生成一群决策树的过程中，如果我们又满足了样本随机和特征随机，那么构建好的这一批决策树，我们就称为随机森林(Random Forest)。

实际上，我们也可以使用SVM，逻辑回归等作为分类器，这些分类器组成的总分类器，我们习惯上依旧称为随机森林。