误差反向传播算法
通过单个感知机或者单层神经网络只能够实现线性分类的问题,而多层神经网络可以解决非线性分类问题。
神经网络中的模型参数,是神经元模型中的连接权重以及每个功能神经元的阈值,
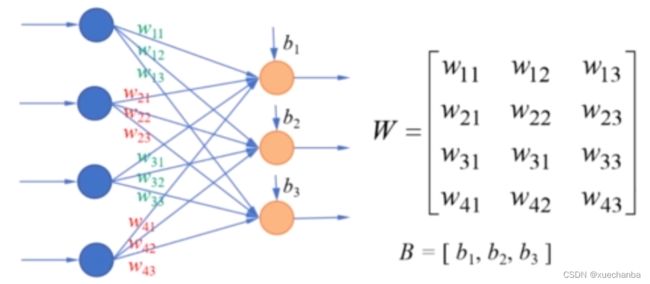
这些模型参数并不是我们人工设计或者指定的,而是通过算法自动学习到的。
和其他机器学习算法一样,神经网络的训练,就是给定训练集,通过学习算法,确定学习参数的过程。可以直接使用梯度下降法需要计算损失函数的梯度,在没有隐含层的单层神经网络中,可以通过计算直接得到梯度。
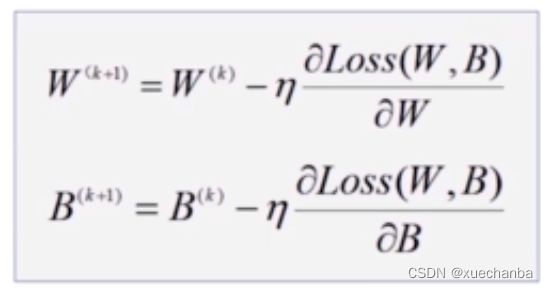
在多层神经网络中,上一层的输出是下一层的输入,要在网络中的每一层计算损失函数的梯度会非常的复杂,
为了解决这个问题,科学家提出一种解决方法,即利用链式法则,反向传播损失函数的梯度信息,只要从后往前遍历一遍神经网络,就能够计算出损失函数对网络中所有模型参数的梯度。这种方法被称之为误差反向传播算法。
需要注意的是,很多人认为误差反向传播算法是多层神经网络的学习算法。这是不对的。
误差反向传播算法仅仅是一种在神经网络的训练过程中用来计算梯度的方法,它能够计算损失函数对网络中所有模型参数的梯度,这个梯度会反馈给某种学习算法,例如梯度下降法,用来更新权值,最小化损失函数,这里梯度下降法才是学习算法,除了梯度下降法,也可以采用其他的学习算法。另外,误差反向传播法并不仅仅适应于多层神经网络,原则上它可以计算任何函数的导数。
为了便于理解,我们首先来看一个简单的例子,
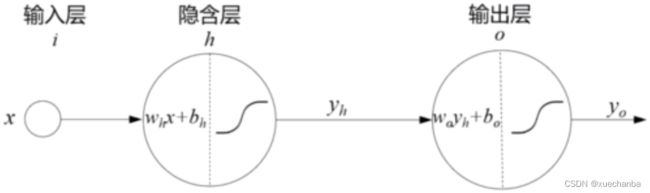
上图为一个最简单的两层神经网络。它的输入层、隐含层和输出层都只有一个节点。隐含层和输出层的激活函数都使用 Sigmoid 函数,隐含层神经元接收输入值 x ,
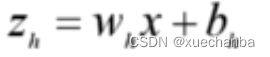
首先,进行线性变换,然后将线性变换的结果 zh 作为激活函数函数的输入,从而产生隐含层的输出 yh ,
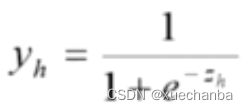
输出层神经元接收隐含层的输出yh 作为输入,对其进行线性变换,产生zo ,

然后再将 zo 作为激活函数函数的输入,从而产生神经网络的输出 yo 。
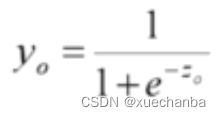
这个神经网络中的所有模型参数是 wh ,bh ,wo ,bo .
训练的过程就是将样本数据x输入网络中,从而通过学习算法,寻找合适的模型参数,使得网络的输出yo 与样本数据的标签一致。
假设现在有一个样本

我们将其输入到这个神经网络中,看看网络是如何进行训练的,
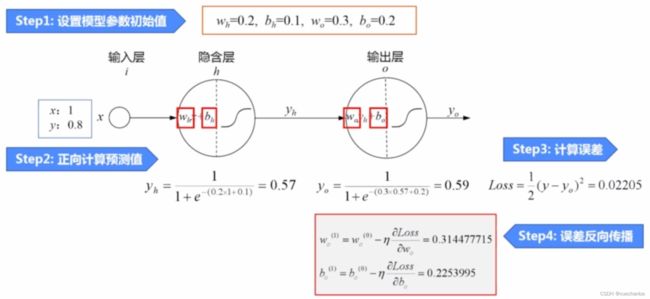
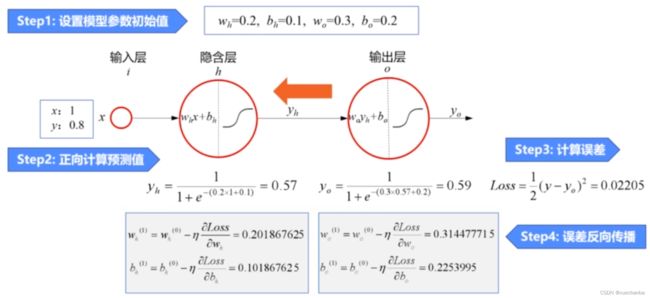
步骤一:设置模型参数初始值
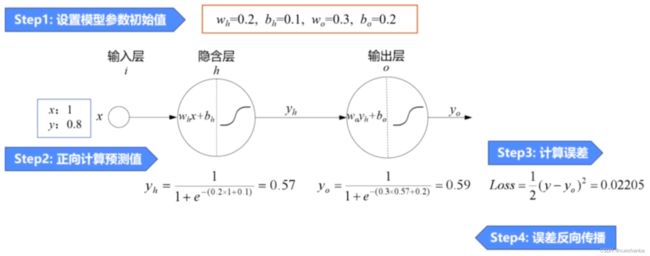
步骤二:正向计算预测值
使用模型参数初始值和输入值x,逐层计算,得到神经网络的预测值0.59,它而样本标签0.8相差比较大,因此需要使用误差函数来调整模型参数,也就是训练网络。
第三步:计算误差
使用平方损失函数计算出预测值和标签值之间的误差。
第四步:误差反向传播
使用误差反向传播算法对误差损失函数的梯度信息进行反向传播,同时更新所有的模型参数,首先更新输出层模型参数。
梯度下降法的参数更新公式如下:

这里要计算误差损失函数对 wo 和 bo 的偏导数,在之前,我们在编程实现逻辑回归时,直接使用了 TensorFlow 中提供的自动求导函数,并没有关心这个倒数是如何计算出来的。
现在,来手动计算一下,
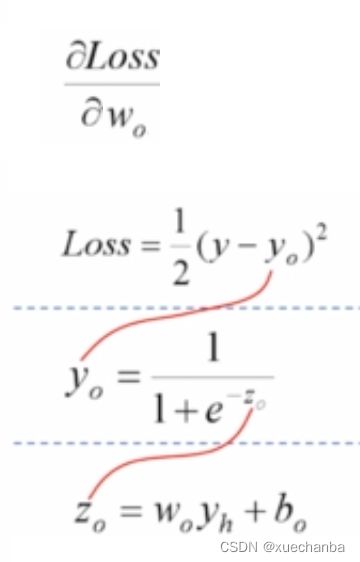
可以发现,这三个函数之间是嵌套的关系,要得到损失函数对wo 的偏导数,可以使用链式求导法则来进行计算。

下面来分别对每一项进行计算。
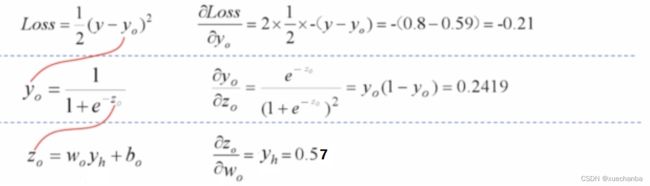
再将这三个得到的值进行相乘,
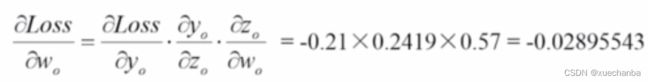
就得到了损失函数对 wo 的偏导数。
取学习率 η 等于 0.5 ,根据迭代公式,更新 wo 的值。

同样的方法可得
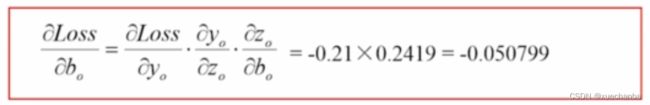
其中,
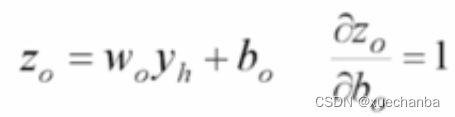
再使用迭代公式更新 bo ,
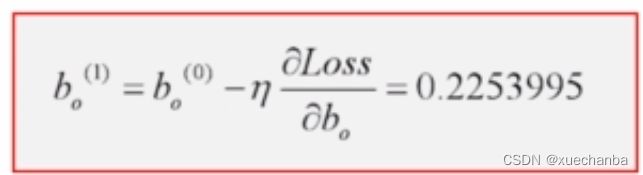
现在,输出层的参数就已经更新好了。
下面,继续更新隐含层的参数,同样,梯度下降法的参数更新公式如下:

这里要计算误差损失函数对 wh 和 bh 的偏导数。
同样可以使用链式求导法则来进行计算。

并且存在下述嵌套关系,
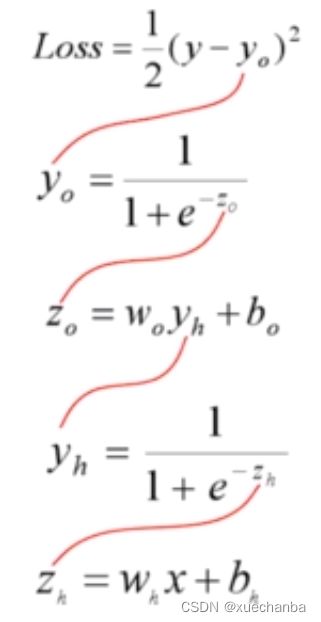
计算其中所有的偏导数,

最后把他们的各自结果代入上面的链式求导公式,

最终求得损失函数对 wh 的偏导数结果,采用同样的方法,最终也可以得到损失函数对 bh 的偏导数。

(计算技巧:与损失函数对 wh 的偏导数公式相比,只有最后一项不同。)
最后代入上述公式可以得到。
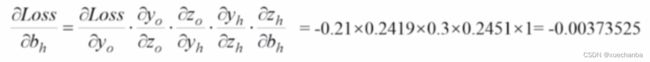
得到
之后,就可以根据迭代公式得到

到此为止,我们已经将这个神经网络中的四个模型参数都更新了,完成了一轮训练。
接下来,再使用新的参数逐层正向计算得到新的预测值,然后和标签值进行比较计算误差,再逐层反向传播损失函数的梯度信息,更新模型参数,完成下一轮训练,如此循环,直到误差收敛到一个理想的值。
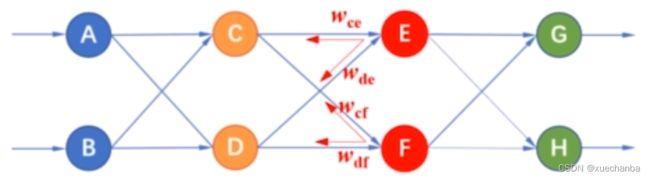
这个神经网络相对简单,每层只有一个神经元,因此,输出层的误差和梯度全部被反向传播给隐含层。
如果隐含层中有多个神经元,那么误差项就会根据不同神经元的贡献程度,进行反向传播。这个贡献程度,是由它们的权值来决定的。
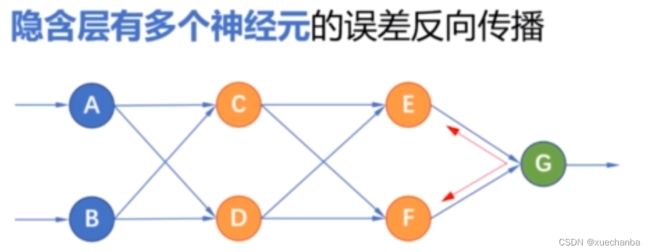
例如,一个是 0.4 ,一个是 0.6
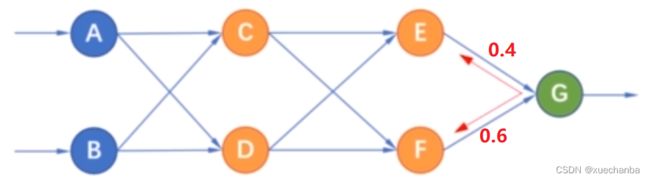
那么就会把输出层的误差按照这个权值的比例分别传递给节点 E 和结点 F,同样隐含层节点 E 的误差,也按照连接的权值分别传递给节点 C 和结点 D。
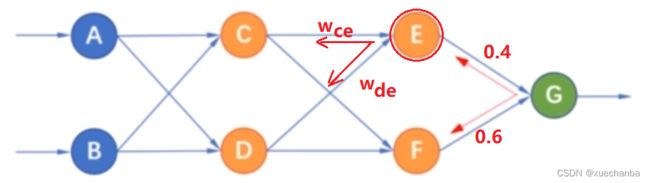
下图分别是节点 C 和结点 D 接收到的来自节点 E 的误差,
结点 F 的误差也按照权值分别传递给节点 C 和结点 D,下图即为节点 C 和结点 D 接收到的来自结点 F 的误差,
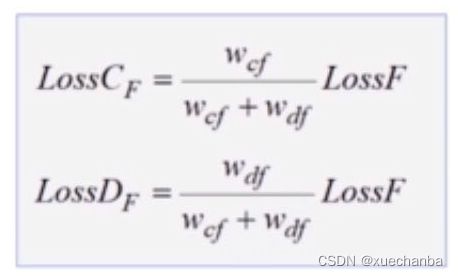
对于节点 C 来说,它分别接收来自节点 E 和 F 传递过来的误差,下图为它接收到的误差,
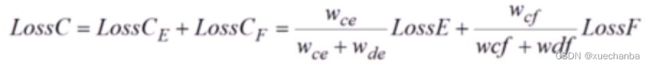
同样对于节点 D 来说,它也是分别接收来自节点 E 和 F 传递过来的误差,下图为它接收到的误差。
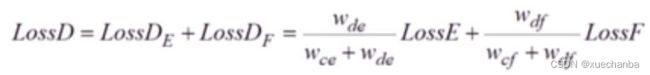
当隐含层中,有多个结点时,神经网络就是这样逐层按照权值反向传播误差的。
如果再复杂一点,输出层也有两个神经元,
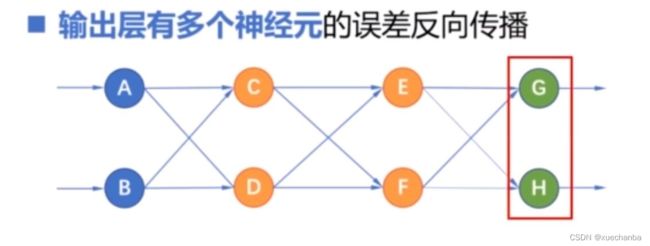
那么输出层结点 G 的误差分别传递给节点 E 和结点 F ,
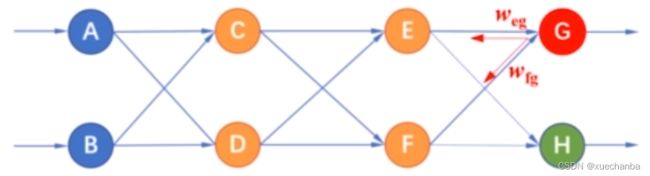
而 H 的误差也分别传递给节点 E 和结点 F ,
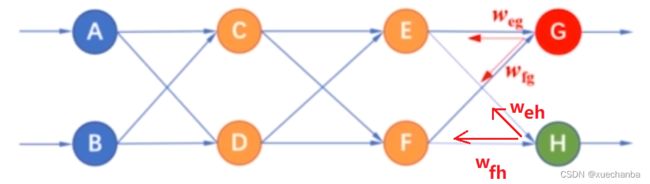
下图分别为 E 和 F 接收到的误差,
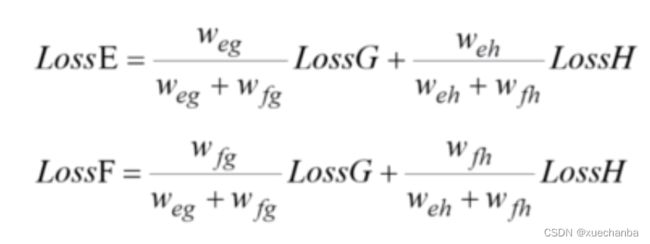
继续按照权值比例逐层反向传递误差。
可以想象,随着网络层数的加深以及每层中神经元个数的增加,误差反向传播算法得计算也会越来越复杂。
幸运的是,TensorFlow 为我们计算梯度的功能,我们在编程时是不需要这样手动推导公式,并且编写代码实现的。
总结一下,这节课的内容,就是多层神经网络的训练是通过梯度下降法训练模型参数,其中,梯度的计算是通过误差反向传播算法来进行的。训练的过程可以概括为:正向传递信号,反向传递误差。
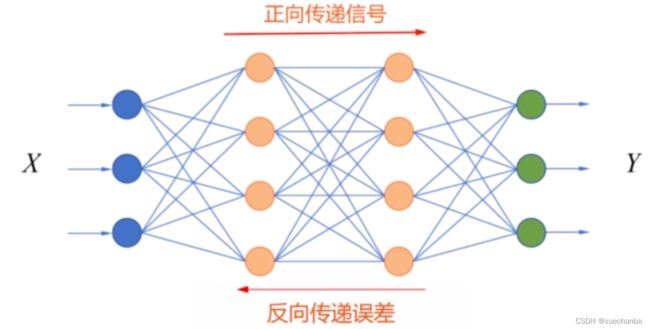
首先,在输入层接收输入样本特征 X ,然后在神经网络中逐层传递,直到在输出层得到预测值 Yo 。 接着将神经网络输出的预测值和 Yo 和标签值 Y 相比较,然后计算损失,
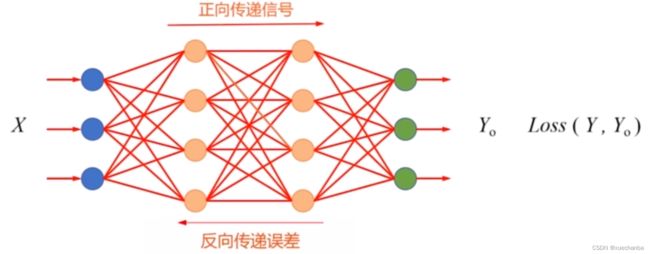
如果损失值比较大,就使用梯度下降法调整最后一层神经元的参数,然后反向传播梯度信息,逐层后退,更新模型参数,完成一轮训练。
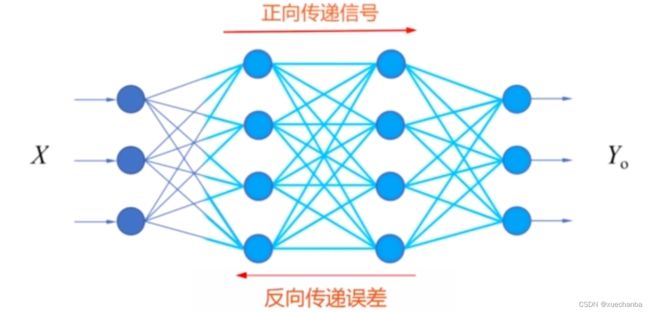
参数调整后的网络,再次根据样本特征,正向计算预测值,反向传播误差,调整模型参数,最终通过这样不断地训练,直到网络输出与标签值一致。
这就好像我们学习,每个人都有自己的学习习惯和学习方法,
比如如何测试,如何写作业,如果做笔记等等,
我们输入的知识就可以当做是 X ,经过这一系列环节之后,迎来一场考试,这就是知识正向传播的过程,输出就是考试的成绩。
如果没有自动更新的能力,那么这个考试成绩就不会去改变学习习惯,下次再考,还是这个成绩,而如果具备这种误差反向传播的能力,那么就会根据试卷上的错题,分析自己学习方法的不足,然后一层一层倒回去,调整自己的学习方式和学习习惯,完成对学习活动中各个环节的参数的调整,然后再下一轮的学习中就可以表现的更好,得到一个满意的成绩。
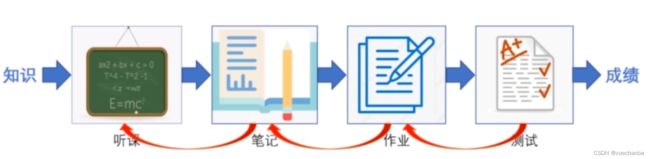
如果泛化能力很强,那么使用这套调整后的学习方法再今后学习不同领域的知识时,也能取得一个好成绩。