<视觉SLAM十四讲> ch7 视觉里程计1
文章目录
-
- 一、特征点法
-
- 1.1 特征点
- 1.2 ORB 特征
- 1.3 特征匹配
- 实践
- 二、 计算相机运动
- 三、2D-2D:对极几何
-
- 3.1 对极约束
- 3.2 本质矩阵
- 3.3 单应矩阵
- 讨论
- 四、实践
- 五、三角测量(Triangulation)
-
- 讨论
- 六、三角测量实践
- 七、3D-2D:PnP
-
- 7.1 直接线性变换
一、特征点法
特征点法特征:稳定,对光照、动态物体不敏感。
1.1 特征点
特征点:有代表性的点。视觉SLAM称这些点为路标(图像特征feature)。
特征点性质:不同的图像可以找到相同的特征(可重复性),不同特征有不同的表达(可区别性),特征点数量不多(高效率),特征仅与一小片图像区域相关(本地性)。
特征点主要包括 关键点(key-point, 该特征点在图像中的位置) + 描述子(descriptor,该特征点长什么样子)
比如:① SIFT(尺度不变特征变换):计算量大但考虑充分;
② FAST:快且没描述子;
③ ORB:Oriented FAST and Rotated BRIEF,速度还可以且特征子具有旋转、尺度不变性。
1.2 ORB 特征
提取ORB特征分两步骤:Fast角点提取+BRIEF描述子。
FAST关键点:
主要思想:比较一个像素 I p I_p Ip和邻域像素的亮度。在半径为3的16个像素点比较亮度,连续12个点的亮度大于 I p + T I_p+T Ip+T或小于 I p − T I_p-T Ip−T则认定为角点。FAST-12为了更快,直接检测1,5,9,13个像素的亮度,只有4个像素中有3个同时大于 I p + T I_p+T Ip+T或小于 I p − T I_p-T Ip−T,当前像素才可能是角点。此外为了预防FAST角点出现扎堆的情况,用非极大值抑制,可以在一定区域内保留相应极大值的角点。
缺点:不具有方向性和尺度。
ORB添加尺度不变性:构建图像金字塔;
ORB添加旋转的描述:添加质心。
BRIEF描述子
1.3 特征匹配
最简单的特征匹配方法是暴力匹配,计算每个特征点描述子的距离,排序,找个最近的作为匹配点。这个方法计算量太大,**快速近似最近邻(FLANN)**更适合匹配点极多的情况。
实践
#include detector = ”等价于 “FeatureDetector * detector =”
Ptr是OpenCV中使用的智能指针模板类,可以轻松管理各种类型的指针。
特征检测器FeatureDetetor是虚类,通过定义FeatureDetector的对象可以使用多种特征检测及匹配方法,通过create()函数调用。
描述子提取器DescriptorExtractor是提取关键点的描述向量类抽象基类。
描述子匹配器DescriptorMatcher用于特征匹配,"Brute-force-Hamming"表示使用汉明距离进行匹配。
**/
//第一步,检测Oriented Fast角点位置
chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
detector->detect(img_1, keypoints_1); //对参数1图像进行特征的提取,并存放入参数2的数组中
detector->detect(img_2, keypoints_2);
//第二步,根据角点计算BREIF描述子
descriptor->compute(img_1, keypoints_1, descriptors_1); //computer()计算关键点的描述子向量(注意思考参数设置的合理性)
descriptor->compute(img_2, keypoints_2, descriptors_2);
chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
cout << "extract ORB cost = " << time_used.count() << " seconds. " << endl;
Mat outimg1;
drawKeypoints(img_1, keypoints_1, outimg1, Scalar::all(-1), DrawMatchesFlags::DEFAULT);
imshow("ORB features", outimg1);
imwrite("feaure1.png", outimg1);
//第三步, 对两幅图像中的描述子进行匹配,使用hamming距离
vector<DMatch> matches; //DMatch是匹配关键点描述子 类, matches用于存放匹配项
t1 = chrono::steady_clock::now();
matcher->match(descriptors_1, descriptors_2, matches); //对参数1 2的描述子进行匹配,并将匹配项存放于matches中
t2 = chrono::steady_clock::now();
time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
cout << "match the ORB cost: " << time_used.count() << "seconds. " << endl;
//第四步,匹配点对筛选
//计算最小距离和最大距离
auto min_max = minmax_element(matches.begin(), matches.end(),
[](const DMatch &m1, const DMatch &m2){ return m1.distance < m2.distance; });
// auto 可以在声明变量的时候根据变量初始值的类型自动为此变量选择匹配的类型
// minmax_element()返回指向范围内最小和最大元素的一对迭代器。参数1 2为起止迭代器范围
// 参数3是二进制函数,该函数接受范围内的两个元素作为参数,并返回可转换为bool的值。
// 返回的值指示作为第一个参数传递的元素是否小于第二个。该函数不得修改其任何参数。
double min_dist = min_max.first->distance; // min_max存储了一堆迭代器,first指向最小元素
double max_dist = min_max.second->distance; // second指向最大元素
printf("-- Max dist : %f \n", max_dist);
printf("-- Min dist : %f \n", min_dist);
//当描述子之间的距离大于两倍最小距离时,就认为匹配有误。但有时最小距离会非常小,所以要设置一个经验值30作为下限。
vector<DMatch> good_matches; //存放良好的匹配项
for(int i = 0; i < descriptors_1.rows; ++i){
if(matches[i].distance <= max(2 * min_dist, 30.0)){
good_matches.push_back(matches[i]);
}
}
//第五步,绘制匹配结果
Mat img_match; //存放所有匹配点
Mat img_goodmatch; //存放好的匹配点
// drawMatches用于绘制两幅图像的匹配关键点。
// 参数1是第一个源图像,参数2是其关键点数组;参数3是第二张原图像,参数4是其关键点数组
// 参数5是两张图像的匹配关键点数组,参数6用于存放函数的绘制结果
drawMatches(img_1, keypoints_1, img_2, keypoints_2, matches, img_match);
drawMatches(img_1, keypoints_1, img_2, keypoints_2, good_matches, img_goodmatch);
imshow("all matches", img_match);
imshow("good matches", img_goodmatch);
imwrite("match1.png", img_match);
imwrite("goodmatch1.png", img_goodmatch);
waitKey(0);
return 0;
}
二、 计算相机运动
单目:根据两组2D点,用对极几何。
双目、RGB-D:根据两组3D点,用ICP。
一组3D、一组2D:用PnP。
三、2D-2D:对极几何
3.1 对极约束
基础矩阵(Fundamental Matrix)F
本质矩阵(Essential Matrix)E
p 像素点 , x 归一化平面的点
![]()
E 和 F 只相差相机内参K,相机位姿估计问题:
- 根据配对点的像素位置求出E 或 F。
- 根据E 或 F 求出R 和 t。
3.2 本质矩阵
E是一个3*3的矩阵,内有9个未知数。
- 对极约束是等式为0的约束,E乘以任何非零常数后对极约束仍然满足。E 在不同尺度下等价。
- 本质矩阵的内在性质:E的奇异值必定是 [ σ , σ , 0 ] T [\sigma, \sigma, 0]^T [σ,σ,0]T的形式。
- 平移和旋转各有3个自由度,即E有6个自由度,由于尺度等价性,E实际上有5个自由度。即最少用5对点来求解E。
用八点法来估计E。线性代数的方法,E展开写成向量的形式,8个方程构成一个线性方程,利用线性性质求解。
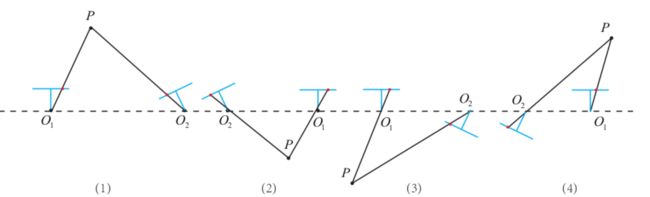
用E恢复R和t。存在两个可能的t和R。
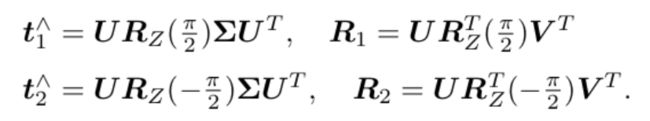
四个解如图,将任意点带入,检测该点在两个相机下的深度,就可以确定哪个正确。
另,八点法求出的E可能不满足内在性质,因此会把E调整下,设奇异值矩阵为 d i a g ( σ 1 , σ 2 , σ 3 ) diag(\sigma1, \sigma2, \sigma3) diag(σ1,σ2,σ3),得到 E = U d i a g ( σ 1 + σ 2 2 , σ 1 + σ 2 2 , 0 ) V T E = Udiag(\frac{\sigma1+\sigma2} 2,\frac{\sigma1+\sigma2} 2,0)V^T E=Udiag(2σ1+σ2,2σ1+σ2,0)VT, 更简单的做法是取diag(1,1,0)。
另,F具有7个自由度。
3.3 单应矩阵
描述两个平面之间的映射关系。通常描述共处于共同平面上的一些点在两张图象之间的变换关系。
讨论
E和F之间相差了相机内参矩阵,E、F、H都能分解运动,不过H需要假设特征点位于平面上。E本身具有尺度等价性,分解得到的t和R也具有尺度等价性,通常让t进行归一化,让他的长度为1。
尺度不确定性
对t长度归一化,即固定了尺度。也被称为单目SLAM的初始化。初始化的两张图像必须有一定程度的平移,而后的轨迹和地图都以此的平移为单位。另一种初始化的方法是所有特征点平均深度为1。相比较t=1的做法,特征点归一化可以控制场景规模大小。
初始化的纯旋转问题
纯旋转,t=0,E=0。R也求不出来。总之初始化的话,不能只有旋转,必须加一定程度的平移。
多于8对点的情况
给定的匹配点多于8则构成一个超定方程,可以最小化一个二次型来求。不过当可能存在误匹配的情况,倾向于用随机采样一致性(Random Sample Concensus, RANSAC),适用于带错误数据的情况。
四、实践
略
五、三角测量(Triangulation)
单目SLAM仅通过单张图像无法得到像素的深度信息,因此需要用三角测量的方法估计地图点的深度。通过不同位置对同一路标点进行观察,从观察的位置推断路标点的距离。
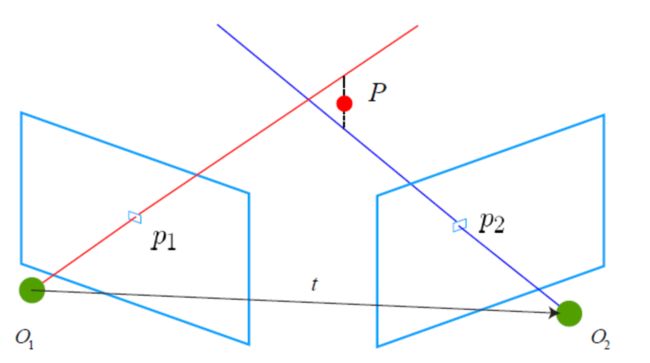
x1和x2是两个特征点归一化坐标,s1和s2是两个特征点深度。运动后: s 1 x 1 = s 2 R x 2 + t s_1x_1 = s_2Rx_2+t s1x1=s2Rx2+t
若先算s2, 右侧只有s2,可以直接求s2。其实更常见是用最小二乘法求解。
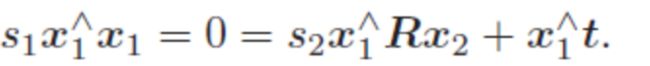
讨论
三角测量是由平移得到的,平移越大,三角测量越准确。为了提高三角化的精度,一种是提高特征点的提取精度,另一种是使平移量增大。
六、三角测量实践
略
七、3D-2D:PnP
前面提到2D-2D的对极几何需要8点或8以上点对,需要初始化、纯旋转和尺度的问题。但是如果其中一张图像中的3D位置已知,那么最少需要3对点即可。再双目或RGB-D的视觉里程计中直接使用PnP估计运动。
求解方法有:直接线性变换(DLT)、EPnP(Efficient PnP)、光束法平差(Bundle Adjustment,BA)等。
7.1 直接线性变换
**问题描述:**一组3D点的位置 P = ( X , Y , Z , 1 ) T P = (X,Y,Z,1)^T P=(X,Y,Z,1)T,另一个坐标系中的平面位置(投影位置) x 1 = ( u 1 , v 1 , 1 ) T x_1 = (u_1,v_1,1)^T x1=(u1,v1,1)T,求解两个相机的相对运动问题 [ R ∣ t ] [R|t] [R∣t]。
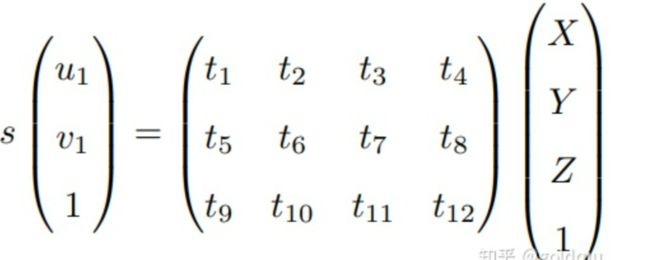
主要步骤:
把定义 T T T行向量为 t 1 , t 2 , t 3 t_1, t_2, t_3 t1,t2,t3,
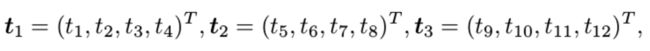
t 1 T P − t 3 T P u 1 = 0 t_1^TP-t_3^TPu_1=0 t1TP−t3TPu1=0 和 t 2 T P − t 3 T P u 1 = 0 t_2^TP-t_3^TPu_1=0 t2TP−t3TPu1=0