数据结构与算法(第一章)——绪论
注:本学习资料依据教材《数据结构(C语言版|第2版)》(严蔚敏 李冬梅 吴伟民 著)
导语:
算法是编程的灵魂,计算机专业的学生都将学习数据结构与算法这门课,知己知彼,百战百胜,那么在学习本门课之前,首先要理解这门课究竟在学什么:
数据结构与算法,顾名思义,数据结构指的是“一组数据的存储结构”,算法指的是“操作数据的一组方法”。了解了数据结构,能设计出更优的算法,有了更好的算法,能作用在特定的数据结构上,二者联系紧密,相辅相成。
这门课在计算机专业本科的学习中也占据着重要的作用,为之后的Web信息处理、人工智能、图形图像、数据库、操作系统、编译原理等学习奠定了基础。
1.1 基本概念和术语
1、数据(Data):所有能输入到计算机中去的描述客观事物的符号。包括数值型数据(如整数、实数等能进行加减乘除运算的数据)和非数值型数据(如文字、图像、图形、声音等,非数值型数据需要经过特殊编码定义)
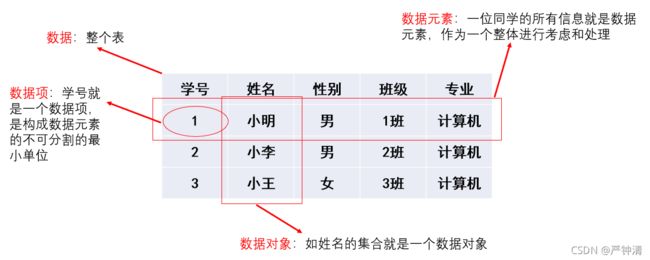
2、数据元素(Data Element):数据的基本单位,也称为元素、结点、记录等。如学生基本信息表中一名学生的所有信息(包括学号、姓名、性别、班级、籍贯、专业等信息)。
3、数据项(Data Item):组成数据元素的、有独立含义的、不可分割的最小单位。如学生的学号、姓名等。
由三者的定义可知三者的关系为:数据>数据元素>数据项
4、数据对象(Data Object):性质相同的数据元素的集合,是数据的一个子集(可以是有限集,也可以是无限集)。如所有学生的学号组成的集合。
下面用一个示例来解释这些概念的具体含义:
5、数据结构(Data Structure):是相互之间存在一种或多种特定关系的数据元素的集合(本质是一个集合)。数据结构是带“结构”的数据元素的集合,“结构”就是数据元素之间存在的关系。
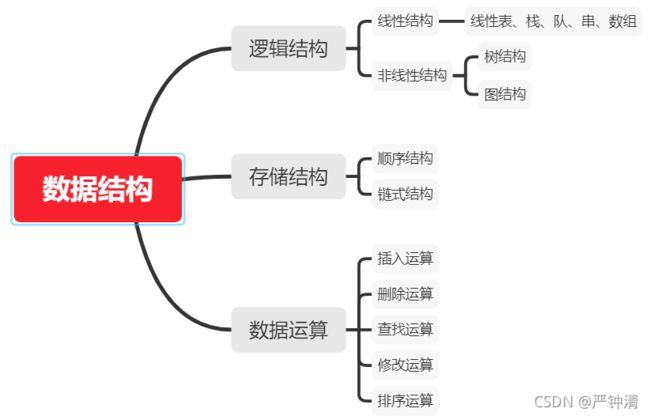
1.2 数据结构
1、逻辑结构:数据的逻辑结构是指数据元素之间的逻辑关系。逻辑结构一般分为线性结构和非线性结构。
(1)线性结构:有且只有一个头结点和一个尾结点,并且所有结点都最多只能有一个前驱结点和一个后继结点。
线性结构特征:在一个具有线性结构的非空有限数据集合中,
a.存在唯一个头元素和唯一的尾元素;
b.除头元素之外,集合中其他元素均只有一个前驱元素;
c.除尾元素之外,集合中其他元素均只有一个后继元素;
(2)非线性结构:相对应于线性结构,非线性结构的逻辑特征是一个结点元素可能对应多个直接前驱和多个直接后继。如树、图等。
2、存储结构:数据对象在计算机中的存储表示,也称为物理结构。常见的有两种基本的存储结构——顺序存储结构和链式存储结构。
(1)顺序存储结构:把逻辑上相邻的结点存储在计算机上相邻的存储单元之中,数据元素之间的关系由存储单元的之间的相邻关系来表示,由此得到的存储结构即为顺序存储结构。最常见的为数组。
顺序存储的优点:
a.节省存储空间,不需要额外空间的来反映元素之间的对应关系,元素之间的关系通过在存储空间的相对位置来反映。
b.对空间上的数据元素存取方便,可通过计算直接定位要存取的元素的位置。
顺序存储的缺点:
a.插入和删除操作需要移动元素,效率较低。
b.存储空间固定,存储元素少,可能造成空间浪费;存储元素过多,则无法扩容,需要另外准备一块足够的存储空间。
(2)链式存储结构:数据元素存储在不连续的存储空间上,每个结点对应一个需要存储的数据元素。结点由数据元素和指针域(一般为前驱或后继结点地址)组成,元素之间的逻辑关系由各个结点之间的链接关系表示。其特点是,每个结点的所在存储空间不必相邻。
链式存储的优点:
a.插入、删除结点灵活简单,只需改变指针域即可。
b.空间利用率高,不会有闲置结点,有元素才会分配结点空间,无需关注扩容和空间浪费问题。
链式存储的缺点:
a.每个元素占用空间相对顺序存储高,需要存储元素之间的关系(指针域)。
b.查询元素时相对较慢,只能遍历查找。
1.3 算法和算法分析
1、算法的定义及特性
(1)算法的定义:为了解决某类问题而规定的一个有限长的操作序列。
(2)算法需满足:有穷性、确定性(每步定义都是确切、无歧义的)、可行性(又称有效性,即算法可以实现)、输入(零个或多个输入)、输出(一个或多个输出,可理解为反馈结果)。
2、评价算法优劣的基本标准:正确性、可读性、健壮性(能好地报错)、高效性(时间代价和空间代价两个维度)。
3、算法的时间复杂度
(1)问题规模:算法求解问题输入量的多少(这是问题大小的本质表示)。问题规模是影响时间代价的最主要因素。
(2)语句频度:一条语句的重复执行次数。
(3)时间复杂度定义:算法中基本语句重复执行的次数记作f(n),则T(n)=O(f(n))成为时间复杂度。
4、算法的空间复杂度
定义:算法需要占用的辅助空间大小的函数:S(n)=O(f(n))
有关算法的复杂度计算问题将在后续更新。