哈弗曼树与哈弗曼编码

哈弗曼，一个在几乎所有讲数据结构的书中都有出现过的人物，他的鼎鼎大名想必就不用我多说了。这一次来给大家讲解一下哈弗曼树的构建与哈弗曼编码的基本原理，有什么用呢？别急，还是先学会创建一棵哈弗曼树吧。

哈弗曼树又称最优二叉树，最优二叉树就是带权路径长度WPL最小的二叉树，那么我们就得搞清几个概念：

1. 路径长度：从树中的一个结点到另一个结点之间的分支构成这两个结点的路径，路径上的分支数目称为路径长度。

2. 树的路径长度：从树根到每一个结点的路径长度之和，我们所说的完全二叉树就是这种路径长度最短的二叉树。

3. 树的带权路径长度：如果在树的每一个叶子结点上赋上一个权值，那么树的带权路径长度就等于根结点到所有叶子结点的路径长度与叶子结点权值乘积的总和。

 

那么我们怎么判断一棵树是否为最优二叉树呢，先看看下面几棵树
 

他们的带权长度分别为：

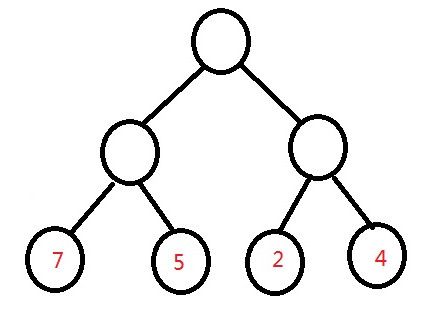
WPL1：7*2+5*2+2*2+4*2=36

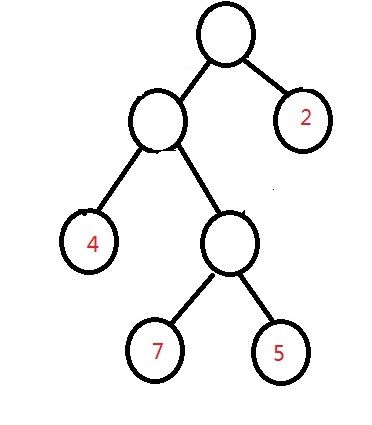
WPL2：7*3+5*3+2*1+4*2=46

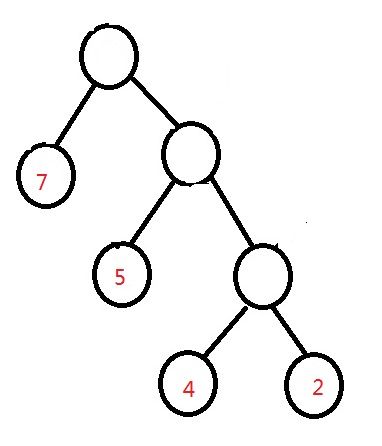
WPL3：7*1+5*2+2*3+4*3=35

很明显，第三棵树的带权路径最短，这就是我们所说的最优二叉树（哈弗曼树），它的构建方法很简单，依次选取权值最小的结点放在树的底部，将最小的两个连接构成一个新结点，需要注意的是构成的新结点的权值应该等于这两个结点的权值之和，然后要把这个新结点放回我们需要构成树的结点中继续进行排序，这样构成的哈弗曼树，所有的存储有信息的结点都在叶子结点上。

下面一张图片就为大家演示了哈弗曼树的构建过程：

 

 

看了这么多，我们再来看看哈弗曼树的代码实现吧，假设我们要把一个数组中的元素封装到哈弗曼树中，那么我们需要做下面几件事：

       1.  有一个容器来存放我们的哈弗曼树的结点

       2.  有一个方法能够比较各个结点的权值大小进行排序

       3．有一个打印二叉树结点的方法（先序，中序或者后序）

       4．我们先要做一个测试用例，判断我们最后的结果是否正确

       胡zong也总是教导我们，学会分析问题远远比代码本身更重要，分析问题的同时也体现了你的逻辑思维，最开始学习编程的时候，可能更多的时候是拿到一个问题先去写，再来发现问题，但是学习了一段时间之后，更加全面的考虑问题往往比解决当前问题更重要。

       好的，不扯太远了，java的API中有一个优先队列（PriorityQueue<E>）的类，它的构造方法中有一个是可以放入一个比较器类比较队列中的元素，然后把最小的放到队列的头部，那么我们要进行一二步就变得简单了，如下：

//定义一个优先级队列来保存结点
PriorityQueue<TNode> queue=new PriorityQueue<TNode>(11,new MyComparator());
//创建一个比较器类
class MyComparator implements Comparator<TNode>{
    public int compare(TNode n1,TNode n2){
        return n1.data-n2.data;
    }
}

打印树的结点的方法更简单：

/**
 * 先序遍历二叉树
 */
public void PreOrderTraverse(TNode root){
    if(root!=null){
        System.out.print(root.data+" ");
        PreOrderTraverse(root.lchild);
        PreOrderTraverse(root.rchild);
    }
}

最后就是我们的最重要的方法了：

/**
 * 将数组中的元素封装到哈弗曼树种
 * @param arr 传入的数组元素
 * @return 哈弗曼树的根结点
 */
public TNode CreateHuffmanTree(int arr[]){
    for(int i=0;i<arr.length;i++){
    //将数组元素封装到队列当中
                 TNode node=new TNode(arr[i]);
        queue.add(node);
    }
    //如果队列的长度大于2则获取最小的两个结点
    while(queue.size()>=2){
                    TNode lnode=queue.poll();
        TNode rnode=queue.poll();
        //将元素最小的两个结点连接起来产生一个新的结点
        TNode node=new TNode(lnode.data+rnode.data);
                       node.lchild=lnode;
            node.rchild=rnode;    
            queue.add(node);
    }
    //如果只剩最后一个结点，那么这个结点就是根结点
    TNode node=queue.poll();
    return node;
}

 还有结点类：

class TNode{
    int data;//数据域
    TNode lchild,rchild;//左右孩子结点
    public TNode(int data){
        this.data=data;
    }
}

讲完了这些，相信大家对于哈弗曼树也有了一定的认识，下面再简单讲解一下哈弗曼编码，至于编码的具体作用将在下次博客中提到：

构建好一颗二叉树后我们就可以对其进行编码了，编码的方式有两种：

1.       对所有的左子树路径都编码为1，右子树路径都编码为0。

2.       与第一条相反。

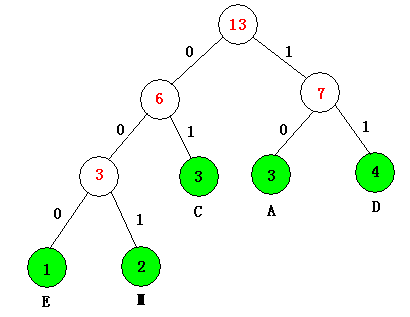
叶子结点的哈弗曼编码就是从根结点到该结点所经过的所有路径的编码的顺序组合。由于所经过的路径不可能重复，所以每一个叶子结点所对应的编码都是唯一的，而且，更重要的是，任意一个叶子结点的编码都不是其他叶子结点的前缀，这种编码叫做前缀编码。

如下就是一棵编码好的哈弗曼树：

    如E结点的编码就是000，C的编码就是01。。。

    好了，希望大家也能一起不断的汲取知识，软件行业，年轻的心需要更多的Energy。编程与就像体育锻炼一样，我们需要充满激情。