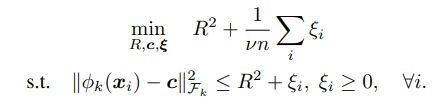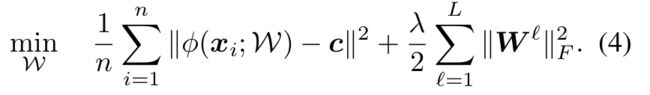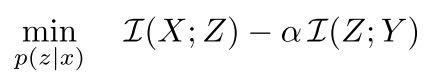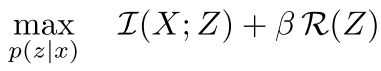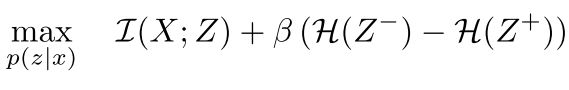- JavaScript 中,深拷贝(Deep Copy)和浅拷贝(Shallow Copy)
跳房子的前端
前端面试javascript开发语言ecmascript
在JavaScript中,深拷贝(DeepCopy)和浅拷贝(ShallowCopy)是用于复制对象或数组的两种不同方法。了解它们的区别和应用场景对于避免潜在的bugs和高效地处理数据非常重要。以下是对深拷贝和浅拷贝的详细解释,包括它们的概念、用途、优缺点以及实现方式。1.浅拷贝(ShallowCopy)概念定义:浅拷贝是指创建一个新的对象或数组,其中包含了原对象或数组的基本数据类型的值和对引用数
- 深度学习-点击率预估-研究论文2024-09-14速读
sp_fyf_2024
深度学习人工智能
深度学习-点击率预估-研究论文2024-09-14速读1.DeepTargetSessionInterestNetworkforClick-ThroughRatePredictionHZhong,JMa,XDuan,SGu,JYao-2024InternationalJointConferenceonNeuralNetworks,2024深度目标会话兴趣网络用于点击率预测摘要:这篇文章提出了一种新
- 探索未来,大规模分布式深度强化学习——深入解析IMPALA架构
汤萌妮Margaret
探索未来,大规模分布式深度强化学习——深入解析IMPALA架构scalable_agent项目地址:https://gitcode.com/gh_mirrors/sc/scalable_agent在当今的人工智能研究前沿,深度强化学习(DRL)因其在复杂任务中的卓越表现而备受瞩目。本文要介绍的是一个开源于GitHub的重量级项目:“ScalableDistributedDeep-RLwithImp
- 云服务业界动态简报-20180128
Captain7
一、青云青云QingCloud推出深度学习平台DeepLearningonQingCloud,包含了主流的深度学习框架及数据科学工具包,通过QingCloudAppCenter一键部署交付,可以让算法工程师和数据科学家快速构建深度学习开发环境,将更多的精力放在模型和算法调优。二、腾讯云1.腾讯云正式发布腾讯专有云TCE(TencentCloudEnterprise)矩阵,涵盖企业版、大数据版、AI
- 机器学习VS深度学习
nfgo
机器学习
机器学习(MachineLearning,ML)和深度学习(DeepLearning,DL)是人工智能(AI)的两个子领域,它们有许多相似之处,但在技术实现和应用范围上也有显著区别。下面从几个方面对两者进行区分:1.概念层面机器学习:是让计算机通过算法从数据中自动学习和改进的技术。它依赖于手动设计的特征和数学模型来进行学习,常用的模型有决策树、支持向量机、线性回归等。深度学习:是机器学习的一个子领
- el-dialog高度设置
夏之小星星
前端vue.jselementuicss
el-dialog高度设置::v-deep.el-dialog{height:78vh;overflow:auto;}
- elementuiPlus取消el-input的边框
qq_39016177
elementui
elementuiPlus取消el-input的边框1.通常取消边框的方法设置border为none2.还有其他类似边框的例如outlinebox-shadow这两个属性都是会产生边框效果3.el-input需要更改的话–如下需要修改box-shadow为空即可上代码:deep(.el-input__wrapper){align-items:center;background-color:#F7F
- 【双语新闻】AGI安全与对齐,DeepMind近期工作
曲奇人工智能安全
agi安全llama人工智能
我们想与AF社区分享我们最近的工作总结。以下是关于我们正在做什么,为什么会这么做以及我们认为它的意义所在的一些详细信息。我们希望这能帮助人们从我们的工作基础上继续发展,并了解他们的工作如何与我们相关联。byRohinShah,SebFarquhar,AncaDragan21stAug2024AIAlignmentForumWewantedtosharearecapofourrecentoutput
- [Kaiming]Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification
MTandHJ
neuralnetworks
文章目录概主要内容PReLUKaiming初始化ForwardcaseBackwardcaseHeK,ZhangX,RenS,etal.DelvingDeepintoRectifiers:SurpassingHuman-LevelPerformanceonImageNetClassification[C].internationalconferenceoncomputervision,2015:1
- 深度神经网络详解:原理、架构与应用
阿达C
活动dnn计算机网络人工智能神经网络机器学习深度学习
深度神经网络(DeepNeuralNetwork,DNN)是机器学习领域中最为重要和广泛应用的技术之一。它模仿人脑神经元的结构,通过多层神经元的连接和训练,能够处理复杂的非线性问题。在图像识别、自然语言处理、语音识别等领域,深度神经网络展示了强大的性能。本文将深入解析深度神经网络的基本原理、常见架构及其实际应用。一、深度神经网络的基本原理1.1神经元和感知器神经元是深度神经网络的基本组成单元。一个
- 前端开发需要了解的算法知识
史努比的大头
算法前端
手写深拷贝functiondeepClone(obj){//处理基础数据类型和函数if(obj===null||typeofobj!=='object'){returnobj;}//处理数组if(Array.isArray(obj)){returnobj.map(item=>deepClone(item));}//处理对象constclonedObj={};for(constkeyinobj){i
- 推荐开源项目:PyTorch-Metric-Learning
潘惟妍
推荐开源项目:PyTorch-Metric-Learningpytorch-metric-learningTheeasiestwaytousedeepmetriclearninginyourapplication.Modular,flexible,andextensible.WritteninPyTorch.项目地址:https://gitcode.com/gh_mirrors/py/pytorc
- LLM系列(4):通义千问7B在Swift/DeepSpeed上微调秘诀与实战陷阱避坑指南
汀、人工智能
LLM工业级落地实践人工智能自然语言处理promptSwifiDeepSpeed通义千问Qwen
LLM系列(4):通义千问7B在Swift/DeepSpeed上微调秘诀与实战陷阱避坑指南阿里云于2023年8月3日开源通义千问70亿参数模型,包括通用模型Qwen-7B以及对话模型Qwen-7B-Chat,这也是国内首个开源自家大模型的大厂。在诸多权威大模型能力测评基准上,如MMLU、C-Eval、GSM8K、HumanEval、WMT22,通义千问7B均取得了同参数级别开源模型中的最好表现,
- 论文学习笔记 VMamba: Visual State Space Model
Wils0nEdwards
学习笔记
概览这篇论文的动机源于在计算机视觉领域设计计算高效的网络架构的持续需求。当前的视觉模型如卷积神经网络(CNNs)和视觉Transformer(ViTs)在处理大规模视觉任务时展现出良好的表现,但都存在各自的局限性。特别是,ViTs尽管在处理大规模数据上具有优势,但其自注意力机制的二次复杂度对高分辨率图像处理时的计算成本极高。因此,研究者希望通过引入新的架构来降低这种复杂度,并提高视觉任务的效率。现
- linux查看jupyter运行,在Linux服务器上运行Jupyter notebook server教程
天启大烁哥
在Linux服务器上运行Jupyternotebookserver教程很多deeplearning教程都推荐在jupyternotebook运行python代码,方便及时交互。但只在本地运行没有GPU环境,虽然googlecolab是个好办法,但发现保存模型后在云端找不到模型文件,且需要合理上网才能访问。于是想给实验室的服务器配置jupyternotebook,供本机远程访问。踩了不少坑,码一下教
- 加载pkl文件,Python报错AttributeError: Can‘t get attribute ‘DeepFM‘ on <module ‘__main__‘ from...>
Zerol_Yan
Python基础python
背景模型同学发过来的pkl格式的模型,在系统中加载的时候,报错AttributeError:module'__main__'hasnoattribute'LabelEncoderExt',尝试了很多种方式,最后终于解决了这个问题,记录一下,以后遇到类似的可以做参考。项目代码及结构app.pyfrominitimportappimportjsonfromflaskimportrequest@app.
- 使用PyTorch实现的DeepSpeech模型: 强大的语音识别利器
毕艾琳
使用PyTorch实现的DeepSpeech模型:强大的语音识别利器deepspeech.pytorchSpeechRecognitionusingDeepSpeech2.项目地址:https://gitcode.com/gh_mirrors/de/deepspeech.pytorch在今天的数字化世界中,语音识别技术已成为人机交互的关键组成部分。deepspeech.pytorch是一个由Sea
- Deepspeed 结合huggingface Trainer实现多机分布式训练
ningzhao
分布式
目前工作中只使用了单机多卡做微调训练,为了提升训练效率,特实验多机多卡分布式训练。一、环境准备本试验使用两台机器(manager,worker),操作系统ubuntu22.4,每台机器有4个GPU为了使安装配置统一,使用docker容器,docker的安装这里不做介绍。1.网络配置-创建overlay共享网络初始化集群,在manager机器上运行:dockerswarminit#输出结果:Swar
- 大模型多机多卡脚本实例 - 增量预训练 -accelerate和deepspeed命令多机多卡训练有什么不同
AI生成曾小健
大模型/增量预训练CPT深度学习python机器学习
第一步,同步权重ls-l/data/xxx/gpu008/MoeRemake/train/etuning/LLaMA-Factory2/models/xxx-Base-10B-200k-Llama第二步,同步环境:./scp_batch.sh"/data/xxx/miniconda3/envs/etuning4/""/data/vayu/miniconda3/envs/etuning4/"gpu0
- Deep learning for Computer Vision with Python(1)从零开始入门计算机视觉
Hazelyu27
计算机视觉大数据计算机视觉深度学习
本书的内容分成三个部分:1.初始阶段初始阶段学习:机器学习、神经网络、卷积神经网络、建立数据集。2.实践阶段实践阶段:深入学习深度学习,理解先进技术,发现最佳实践方式。3.图像网络阶段完成计算机视觉领域的经验积累。使用大规模数据集和真实图片案例作为数据集,包括年龄和性别预测,交通工具模型识别。本书提供了对应网站:http://pyimg.co/fnkxk本文介绍前两章内容:基本介绍和深度学习简介。
- 使用matlab的热门问题
七十二五
值得关注matlab开发语言青少年编程算法经验分享
MATLAB广泛应用于科学计算、数据分析、信号处理、图像处理、机器学习等多个领域,因此热门问题也涵盖了这些方面。以下是一些可能被认为当前最热门的MATLAB问题:深度学习与神经网络:如何使用MATLAB的深度学习工具箱(DeepLearningToolbox)来构建和训练神经网络?如何利用MATLAB进行图像识别、语音识别或自然语言处理等深度学习应用?数据分析与可视化:如何使用MATLAB进行大数
- DeepSeek缓存命中技术,成本降低10倍
智匠MindCraft Al
人工智能gptai功能测试AI编程
DeepSeek系列升级:DeepSeek发布最新的缓存命中技术,有效降低成本至0.1元/百万tokens,适用于文件读取和固定提示词。点评:由于token消耗大部分是在系统提示词中,妥善使用确实可以极大降低成本,同时还能保证较高的输出质量。今天就分享到这里,在智匠AI(MindCraftAI)上可以体验到最新更新的模型。
- COI实验室技能:图像到图像的深度学习开发框架(pytorch版)
山颠海涯
深度学习pytorch人工智能
Basicdeeplearningframeworkforimage-to-image这个开发框架旨在帮助科研人员快速地实现图像到图像之间的模型开发。github连接:https://github.com/SituLab/Basic-deep-learning-framework-for-image-to-image目录1模型开发1-1克隆项目到本地1-2深度学习开发2环境配置2-1安装conda
- auto encoder
war3gu
深度学习
Deepauto-encoder与受限玻尔兹曼机有点像,都可以进行信息的压缩,都可以用作pre-trainning.区别在于受限玻尔兹曼机是无向图模型,而Deepauto-encoder是一种神经网络,中间特别窄的bottleneck的数据作为压缩的codeencoder与decoder的参数可以相互独立,也可以互为逆数字图片auto-encoder,越是deep的auto-encoder,压缩出
- 关于深度森林的一点理解
Y.G Bingo
机器学习方法机器学习神经网络
2017年年初,南京大学周志华老师上传了一篇名为:DeepForest:TowardsAnAlternativetoDeepNeuralNetworks的论文,一石激起千层浪,各大媒体纷纷讨论着,这似乎意味着机器学习的天色要变,实则不然,周志华老师通过微博解释道,此篇论文不过是为机器学习打开了另一扇窗,是另一种思维,而不是真的去替代深度神经网络(DNN)。下面我就简单概括一下我对这篇论文的理解,如
- 【vue使用Sass报错】启动项目报错 Syntax Error: SassError: expected selector
lxx-sissi
vue.jssass前端
出现的问题新项目启动的时候,提示:SyntaxError:SassError:expectedselector看了一下发现是sass使用样式穿透/deep/报的错/deep/其实是已经过期的写法,某个版本之后就不支持了但是我同事并没有出现同样的问题,不知道是为啥,也有可能是电脑(mac)的原因解决办法将/deep/更换为::v-deep但是这个项目是多人协作的,有大量页面使用,修改的话会涉及很多页
- 浅谈lua拷贝
coding·life
Lua初探lua拷贝深拷贝
lua中对象的拷贝分为2种:浅拷贝(ShallowCopy)和深拷贝(DeepCopy)。浅拷贝简单来说只是对一些基本的类型进行复制,而像table这样的类型则直接引用。目前对于浅拷贝有2种说法:1.赋值操作符"="即是浅拷贝2.使用代码实现浅拷贝,代码如下:functionshallow_copy(object)localnewObjectiftype(object)=="table"thenn
- 吐血整理 ChatGPT 3.5/4.0 新手使用手册~ 【2024.09.04 更新】
aiwisland
chatgpt人工智能aiAI编程AI写作
以前我也是通过官网使用,但是经常被封号,就非常不方便,后来有朋友推荐国内工具,用了一阵之后,发现:稳定方便,用着也挺好的。最新的GPT-4o、4omini,可搭配使用~1、最新模型科普:现在人工智能很强大,聊聊天、写论文、搞翻译、写代码、写文案、审合同、情感陪伴等,真是无所不能~本来以为ChatGPT早已普及了,没想到仍然有很多小伙伴还没用上。。。其实使用很简单,可以选通义、智谱、Deepseek
- 【DeepSpeed 教程翻译】三,在 DeepSpeed 中使用 PyTorch Profiler做性能调试和Flops Profiler教程翻译
just_sort
pytorch深度学习人工智能
文章目录0x0.前言0x1.在DeepSpeed中使用PyTorchProfiler做性能调试Profile模型训练的循环标记任意代码范围ProfileCPU/GPU的活动Profile内存消耗0x2.FlopsProfiler总览Flops测量多GPU,多节点,数据并行和模型并行例子和DeepSpeed运行时一起使用在Megatron-LM中使用在DeepSpeed运行环境之外的使用方法在模型推
- halcon深度学习4:深度学习在 OCR的用法-deep_ocr_workflow解析
mlxg99999
halcon深度学习自学
1.什么是OCR技术OCR,全称是OpticalCharacterRecognition,即光学字符识别,面向扫描文件。但是由于现在数字图像的普及,这里泛指文字检测和识别,包括扫描文档和自然场景的文字识别。2、deep_ocr_workflow在深度学习中,只有一篇例子关于OCR就是这一篇,文中介绍了深度OCR模型的建立与使用(如果使用过计量模型的可以较好理解,就是建立模型→设置参数→导入图片→进
- tomcat基础与部署发布
暗黑小菠萝
Tomcat java web
从51cto搬家了,以后会更新在这里方便自己查看。
做项目一直用tomcat,都是配置到eclipse中使用,这几天有时间整理一下使用心得,有一些自己配置遇到的细节问题。
Tomcat:一个Servlets和JSP页面的容器,以提供网站服务。
一、Tomcat安装
安装方式:①运行.exe安装包
&n
- 网站架构发展的过程
ayaoxinchao
数据库应用服务器网站架构
1.初始阶段网站架构:应用程序、数据库、文件等资源在同一个服务器上
2.应用服务和数据服务分离:应用服务器、数据库服务器、文件服务器
3.使用缓存改善网站性能:为应用服务器提供本地缓存,但受限于应用服务器的内存容量,可以使用专门的缓存服务器,提供分布式缓存服务器架构
4.使用应用服务器集群改善网站的并发处理能力:使用负载均衡调度服务器,将来自客户端浏览器的访问请求分发到应用服务器集群中的任何
- [信息与安全]数据库的备份问题
comsci
数据库
如果你们建设的信息系统是采用中心-分支的模式,那么这里有一个问题
如果你的数据来自中心数据库,那么中心数据库如果出现故障,你的分支机构的数据如何保证安全呢?
是否应该在这种信息系统结构的基础上进行改造,容许分支机构的信息系统也备份一个中心数据库的文件呢?
&n
- 使用maven tomcat plugin插件debug关联源代码
商人shang
mavendebug查看源码tomcat-plugin
*首先需要配置好'''maven-tomcat7-plugin''',参见[[Maven开发Web项目]]的'''Tomcat'''部分。
*配置好后,在[[Eclipse]]中打开'''Debug Configurations'''界面,在'''Maven Build'''项下新建当前工程的调试。在'''Main'''选项卡中点击'''Browse Workspace...'''选择需要开发的
- 大访问量高并发
oloz
大访问量高并发
大访问量高并发的网站主要压力还是在于数据库的操作上,尽量避免频繁的请求数据库。下面简
要列出几点解决方案:
01、优化你的代码和查询语句,合理使用索引
02、使用缓存技术例如memcache、ecache将不经常变化的数据放入缓存之中
03、采用服务器集群、负载均衡分担大访问量高并发压力
04、数据读写分离
05、合理选用框架,合理架构(推荐分布式架构)。
- cache 服务器
小猪猪08
cache
Cache 即高速缓存.那么cache是怎么样提高系统性能与运行速度呢?是不是在任何情况下用cache都能提高性能?是不是cache用的越多就越好呢?我在近期开发的项目中有所体会,写下来当作总结也希望能跟大家一起探讨探讨,有错误的地方希望大家批评指正。
1.Cache 是怎么样工作的?
Cache 是分配在服务器上
- mysql存储过程
香水浓
mysql
Description:插入大量测试数据
use xmpl;
drop procedure if exists mockup_test_data_sp;
create procedure mockup_test_data_sp(
in number_of_records int
)
begin
declare cnt int;
declare name varch
- CSS的class、id、css文件名的常用命名规则
agevs
JavaScriptUI框架Ajaxcss
CSS的class、id、css文件名的常用命名规则
(一)常用的CSS命名规则
头:header
内容:content/container
尾:footer
导航:nav
侧栏:sidebar
栏目:column
页面外围控制整体布局宽度:wrapper
左右中:left right
- 全局数据源
AILIKES
javatomcatmysqljdbcJNDI
实验目的:为了研究两个项目同时访问一个全局数据源的时候是创建了一个数据源对象,还是创建了两个数据源对象。
1:将diuid和mysql驱动包(druid-1.0.2.jar和mysql-connector-java-5.1.15.jar)copy至%TOMCAT_HOME%/lib下;2:配置数据源,将JNDI在%TOMCAT_HOME%/conf/context.xml中配置好,格式如下:&l
- MYSQL的随机查询的实现方法
baalwolf
mysql
MYSQL的随机抽取实现方法。举个例子,要从tablename表中随机提取一条记录,大家一般的写法就是:SELECT * FROM tablename ORDER BY RAND() LIMIT 1。但是,后来我查了一下MYSQL的官方手册,里面针对RAND()的提示大概意思就是,在ORDER BY从句里面不能使用RAND()函数,因为这样会导致数据列被多次扫描。但是在MYSQL 3.23版本中,
- JAVA的getBytes()方法
bijian1013
javaeclipseunixOS
在Java中,String的getBytes()方法是得到一个操作系统默认的编码格式的字节数组。这个表示在不同OS下,返回的东西不一样!
String.getBytes(String decode)方法会根据指定的decode编码返回某字符串在该编码下的byte数组表示,如:
byte[] b_gbk = "
- AngularJS中操作Cookies
bijian1013
JavaScriptAngularJSCookies
如果你的应用足够大、足够复杂,那么你很快就会遇到这样一咱种情况:你需要在客户端存储一些状态信息,这些状态信息是跨session(会话)的。你可能还记得利用document.cookie接口直接操作纯文本cookie的痛苦经历。
幸运的是,这种方式已经一去不复返了,在所有现代浏览器中几乎
- [Maven学习笔记五]Maven聚合和继承特性
bit1129
maven
Maven聚合
在实际的项目中,一个项目通常会划分为多个模块,为了说明问题,以用户登陆这个小web应用为例。通常一个web应用分为三个模块:
1. 模型和数据持久化层user-core,
2. 业务逻辑层user-service以
3. web展现层user-web,
user-service依赖于user-core
user-web依赖于user-core和use
- 【JVM七】JVM知识点总结
bit1129
jvm
1. JVM运行模式
1.1 JVM运行时分为-server和-client两种模式,在32位机器上只有client模式的JVM。通常,64位的JVM默认都是使用server模式,因为server模式的JVM虽然启动慢点,但是,在运行过程,JVM会尽可能的进行优化
1.2 JVM分为三种字节码解释执行方式:mixed mode, interpret mode以及compiler
- linux下查看nginx、apache、mysql、php的编译参数
ronin47
在linux平台下的应用,最流行的莫过于nginx、apache、mysql、php几个。而这几个常用的应用,在手工编译完以后,在其他一些情况下(如:新增模块),往往想要查看当初都使用了那些参数进行的编译。这时候就可以利用以下方法查看。
1、nginx
[root@361way ~]# /App/nginx/sbin/nginx -V
nginx: nginx version: nginx/
- unity中运用Resources.Load的方法?
brotherlamp
unity视频unity资料unity自学unityunity教程
问:unity中运用Resources.Load的方法?
答:Resources.Load是unity本地动态加载资本所用的方法,也即是你想动态加载的时分才用到它,比方枪弹,特效,某些实时替换的图像什么的,主张此文件夹不要放太多东西,在打包的时分,它会独自把里边的一切东西都会集打包到一同,不论里边有没有你用的东西,所以大多数资本应该是自个建文件放置
1、unity实时替换的物体即是依据环境条件
- 线段树-入门
bylijinnan
java算法线段树
/**
* 线段树入门
* 问题:已知线段[2,5] [4,6] [0,7];求点2,4,7分别出现了多少次
* 以下代码建立的线段树用链表来保存,且树的叶子结点类似[i,i]
*
* 参考链接:http://hi.baidu.com/semluhiigubbqvq/item/be736a33a8864789f4e4ad18
* @author lijinna
- 全选与反选
chicony
全选
<!DOCTYPE HTML PUBLIC "-//W3C//DTD HTML 4.01 Transitional//EN" "http://www.w3.org/TR/html4/loose.dtd">
<html>
<head>
<title>全选与反选</title>
- vim一些简单记录
chenchao051
vim
mac在/usr/share/vim/vimrc linux在/etc/vimrc
1、问:后退键不能删除数据,不能往后退怎么办?
答:在vimrc中加入set backspace=2
2、问:如何控制tab键的缩进?
答:在vimrc中加入set tabstop=4 (任何
- Sublime Text 快捷键
daizj
快捷键sublime
[size=large][/size]Sublime Text快捷键:Ctrl+Shift+P:打开命令面板Ctrl+P:搜索项目中的文件Ctrl+G:跳转到第几行Ctrl+W:关闭当前打开文件Ctrl+Shift+W:关闭所有打开文件Ctrl+Shift+V:粘贴并格式化Ctrl+D:选择单词,重复可增加选择下一个相同的单词Ctrl+L:选择行,重复可依次增加选择下一行Ctrl+Shift+L:
- php 引用(&)详解
dcj3sjt126com
PHP
在PHP 中引用的意思是:不同的名字访问同一个变量内容. 与C语言中的指针是有差别的.C语言中的指针里面存储的是变量的内容在内存中存放的地址 变量的引用 PHP 的引用允许你用两个变量来指向同一个内容 复制代码代码如下:
<?
$a="ABC";
$b =&$a;
echo
- SVN中trunk,branches,tags用法详解
dcj3sjt126com
SVN
Subversion有一个很标准的目录结构,是这样的。比如项目是proj,svn地址为svn://proj/,那么标准的svn布局是svn://proj/|+-trunk+-branches+-tags这是一个标准的布局,trunk为主开发目录,branches为分支开发目录,tags为tag存档目录(不允许修改)。但是具体这几个目录应该如何使用,svn并没有明确的规范,更多的还是用户自己的习惯。
- 对软件设计的思考
e200702084
设计模式数据结构算法ssh活动
软件设计的宏观与微观
软件开发是一种高智商的开发活动。一个优秀的软件设计人员不仅要从宏观上把握软件之间的开发,也要从微观上把握软件之间的开发。宏观上,可以应用面向对象设计,采用流行的SSH架构,采用web层,业务逻辑层,持久层分层架构。采用设计模式提供系统的健壮性和可维护性。微观上,对于一个类,甚至方法的调用,从计算机的角度模拟程序的运行情况。了解内存分配,参数传
- 同步、异步、阻塞、非阻塞
geeksun
非阻塞
同步、异步、阻塞、非阻塞这几个概念有时有点混淆,在此文试图解释一下。
同步:发出方法调用后,当没有返回结果,当前线程会一直在等待(阻塞)状态。
场景:打电话,营业厅窗口办业务、B/S架构的http请求-响应模式。
异步:方法调用后不立即返回结果,调用结果通过状态、通知或回调通知方法调用者或接收者。异步方法调用后,当前线程不会阻塞,会继续执行其他任务。
实现:
- Reverse SSH Tunnel 反向打洞實錄
hongtoushizi
ssh
實際的操作步驟:
# 首先,在客戶那理的機器下指令連回我們自己的 Server,並設定自己 Server 上的 12345 port 會對應到幾器上的 SSH port
ssh -NfR 12345:localhost:22
[email protected]
# 然後在 myhost 的機器上連自己的 12345 port,就可以連回在客戶那的機器
ssh localhost -p 1
- Hibernate中的缓存
Josh_Persistence
一级缓存Hiberante缓存查询缓存二级缓存
Hibernate中的缓存
一、Hiberante中常见的三大缓存:一级缓存,二级缓存和查询缓存。
Hibernate中提供了两级Cache,第一级别的缓存是Session级别的缓存,它是属于事务范围的缓存。这一级别的缓存是由hibernate管理的,一般情况下无需进行干预;第二级别的缓存是SessionFactory级别的缓存,它是属于进程范围或群集范围的缓存。这一级别的缓存
- 对象关系行为模式之延迟加载
home198979
PHP架构延迟加载
形象化设计模式实战 HELLO!架构
一、概念
Lazy Load:一个对象,它虽然不包含所需要的所有数据,但是知道怎么获取这些数据。
延迟加载貌似很简单,就是在数据需要时再从数据库获取,减少数据库的消耗。但这其中还是有不少技巧的。
二、实现延迟加载
实现Lazy Load主要有四种方法:延迟初始化、虚
- xml 验证
pengfeicao521
xmlxml解析
有些字符,xml不能识别,用jdom或者dom4j解析的时候就报错
public static void testPattern() {
// 含有非法字符的串
String str = "Jamey친ÑԂ
- div设置半透明效果
spjich
css半透明
为div设置如下样式:
div{filter:alpha(Opacity=80);-moz-opacity:0.5;opacity: 0.5;}
说明:
1、filter:对win IE设置半透明滤镜效果,filter:alpha(Opacity=80)代表该对象80%半透明,火狐浏览器不认2、-moz-opaci
- 你真的了解单例模式么?
w574240966
java单例设计模式jvm
单例模式,很多初学者认为单例模式很简单,并且认为自己已经掌握了这种设计模式。但事实上,你真的了解单例模式了么。
一,单例模式的5中写法。(回字的四种写法,哈哈。)
1,懒汉式
(1)线程不安全的懒汉式
public cla

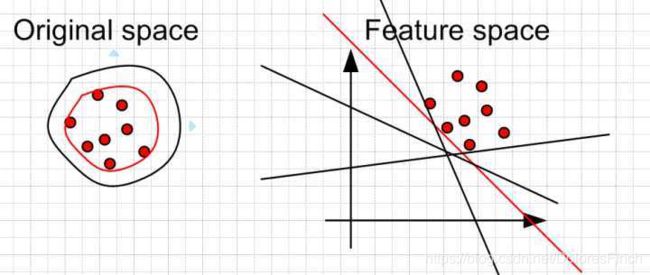
 核函数满足Mercer Theorem
核函数满足Mercer Theorem