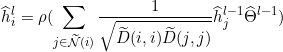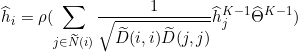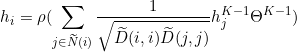Deep Graph-level Anomaly Detection by Glocal Knowledge Distillation

Graph-level anomaly detection, GAD：图级异常检测

Deep support vector data description, Deep SVDD：深度单分类异常检测模型

摘要：GAD是指与其他图相比，检测出结构和/或节点特征异常的图。GAD的挑战之一是设计出能够检测局部和全局异常的图表示，即分别在其细粒度（节点级）或整体（图级）属性上异常的图。为了解决这一问题，作者提出了一种新的深度异常检测方法，该方法通过对图和节点表示的联合随机蒸馏来学习丰富的全局和局部正常模式信息。随机蒸馏是通过训练一个GNN来预测另一个具有随机初始化网络权值的GNN。在来自不同领域的16个真实世界的图数据集上进行的大量实验表明，论文提出的模型显著优于7个最先进的模型。

1 Introduction

GAD的目标是检测出在与集合中大多数图显著不同的图。记录不同实体之间复杂关系的能力使得图成为现实世界中一种重要和广泛使用的表示方式。因此，基于图的异常检测在识别有严重副作用的药物、从化合物中识别有毒分子、破除毒品走私网络等方面有着广泛的应用。

尽管图数据很普遍，其异常检测也很重要，但与其他类型数据的异常检测相比，GAD很少受到关注。GAD的一个主要挑战是学习图表示方法，即在图结构以及属性（如节点的描述性特征）中捕获局部和全局模式。同时检测与节点个体以及他们的邻居节点相关的图局部异常和与整体图特征相关的图全局异常是很有必要的。

一个相关的研究方向是从单个图的时间演化序列中寻找图结构异常变化，其中不同时间步长的大多数节点和结构都是不变的。而GAD则需要在没有时间顺序进程且结构和节点特征多样化的情况下识别出图异常，这类研究明显较少。

深度学习在各种学习任务中取得了巨大的成功，包括最近出现的基于图神经网络GNN的方法。此外，深度异常检测模型如基于自编码器AE的方法，基于生成对抗网络GAN的方法以及一类分类器，在不同类型的的数据集（如表格数据、图像数据和视频数据）上都表现出了良好的性能。然而很少有研究利用GNN探索GAD任务。许多机遇GNN的模型被用于图数据的异常检测，但它们大多关注的是单个大型图中的异常节点/边的检测。

GAD中基于AE和GAN的检测方法的一个挑战是它们对基于重构误差的异常度量的依赖。这是因为从潜在向量表示重构或生成图仍然具有挑战性。如基于一类分类器的Deep SVDD通过直接优化GNN图表示顶层的SVDD对象可以应用于GAD，但它只关注检测图全局异常。因此它的性能很大程度上收到SVDD一类超球面的限制，因为在真实数据集正常类中通常有更复杂的分布。

文章介绍了一种新的GAD深度异常检测方法，该方法能通过对图和节点表示的联合随机蒸馏来同时学习全局和局部正常模式信息。随机表示蒸馏是通过训练一个GNN来预测另一个具有随机初始化固定的网络权值的GNN，即预测器网络学习产生与随机网络相同的表示。为了准确预测这些固定的随机投影表示，预测器网络被强制学习训练数据中的所有主要模式。通过在图和节点表示上应用这种随机蒸馏，模型在给定的训练图上学习全局局部图模式。当训练数据由完全（或大部分）正常图组成时，学习到的模式是汇总的规则/正常的多尺度图信息。因此，当给定的图中节点/图级的模式显示不规则/异常，模型无法准确预测其表示，导致预测误差比正常图大得多。因此，这种预测误差可以被定义为异常分数，用来检测上述两种图异常类型。

据此，文章的主要贡献如下：

（1）将GAD问题表述为检测局部或全局异常图的任务，并在真实数据集上验证这两种图异常类型的存在。

（2）介绍了一种新的深度异常检测框架，对全局局部图规则建模，并以端到端的方式学习图异常分数，设计了第一种专门有效检测两种类型的异常图的方法。

（3）从框架进一步实例化了一种新的GAD模型，即全局和局部知识蒸馏GLocalKD。通过最小化随机图卷积神经网络的图级和节点级预测误差，GLocalKD实现了图和节点表示的联合随机蒸馏。GLocalKD易于实现，不需要具有挑战性的图生成，在训练数据较少的情况下，可以有效地学习多种全局局部正常模式。它对异常干扰也表现出了显著的鲁棒性，表明它在无监督（异常干扰的无标签训练数据）和半监督（完全正常的训练数据）中都具有适用性。

在化学、医学和社交网络领域的16个真实数据集上的广泛实证结果表明：1 GLocalKD显著优于7种最先进的竞争方法；2 与其他深度检测器相比，GLocalKD具有更高的样本效率，如它可以使用少于95%的训练样本来实现精度，仍然显著优于竞争方法；3 GLocalKD使用默认GNN架构，在不同的异常干扰率和表示维度下都非常稳定。

2 Related Work

2.1 Graph-level Anomaly Detection

近年来，基于图的异常检测收到了广泛的关注，尤其是最近出现的基于GNN的异常检测方法，但大多数研究都集中在单个大图上的异常（如异常节点或边）。

Time-evolving Graphs：现有的GAD研究大多是在一系列的时间演化图中识别异常图的变化。然而这些方法被设计来处理具有相似结构的时间图，很难推广到结构和或描述特征有很大变化的图。

Static Graphs：基于静态图的异常检测研究很少。一个研究方向是利用强图表示方法或图核来实现GAD。最近一些研究通过应用现有的异常度量，如孤立森林（iForest）、局部异常因子LOF、一类支持向量机OCSVM在高级图核（如Weisfeiler-Leman核和propagation kernel(PK) ）或图表示学习方法（如Graph2Vec和InfoGraph）的基础上学习的向量化图表示。这些方法的关键问题都是图表示是独立于异常检测学习的，导致了表示的次优表现。另外也有关于GAD的图级模式提取的研究。但是这些方法受到不同领域或应用场景中图级模式的较大区别的限制。

Deep Learning-based Methods：尽管在不同类型的数据中深度异常检测取得了很大的成功，但关于GAD的研究还比较少。深度图学习技术如图卷积网络GCN以及图同构网络GIN，已经成为强大的图表示学习工具，可以应用到不同的下游任务。现有的深度异常检测方法在很大程度上依赖于数据重构/生成模型。因此，图的重构/生成的困难极大的阻碍了GAD深度方法的发展。Zhao等人对GAD进行了大量的评估研究，结果表明Deep SVDD可以应用于基于GNN的图表示以实现GAD。然而，它只关注高层次图表示异常，其性能也受到了SVDD的限制。

2.2 Knowledge Distillation

知识蒸馏的初始目标是训练一个简单的模型，该模型提取大型模型知识的同时能保持与其相似的准确性，在许多研究中扩展到异常检测。这些方法都训练了一个更简单的学生网络，在大规模数据上提取预先训练好的教师网络的知识，如在ImageNet上预先训练的ResNet/VGG网络。但是对于图级数据的学习任务，没有这种经过训练的通用教师网络；此外不同领域的图数据集之间存在显著差异，阻碍了这种方法在GAD任务中的应用。随机知识蒸馏最初引入用于解决深度强化学习DRL中的稀疏奖励问题。它使用随机蒸馏误差来度量新状态，作为额外的奖励信息鼓励DRL代替在稀疏奖励情况下的探索。受此启发，文章设计了GLocalKD模型来共同学习全局局部敏感的图正态性，这是第一种专门设计用于深度图级异常检测两种类型图异常的检测方法。

3 Framework

3.1 Problem Statement

这项研究解决了端到端图级异常检测的问题。首先给定一组个正常图  ，目标是学习一个异常评分函数  ，参数化为  ，例如如果  比  更符合  ，则 。在  中，每个图可以表示为  ，其中  表示向量/节点集， 表示边集。每个图  的图结构可以用邻接矩阵  表示，其中  为图  的节点数。如果  为属性图，则每个节点关联一个特征向量  。 

图集的异常图可以分为两类：

局部异常图：图  中存在某些异常节点  导致不符合  中的图，这些异常节点与  中相似节点有明显的偏差。

全局异常图：图  的整体图性质与  中的图不一致。

我们的目标是训练一个检测模型可以检测这两种类型的异常图。检测局部异常图与检测异常节点是不同的，前者是通过评估节点/边在图集中检测图，后者是在给定的一个图中的节点和边集中检测节点/边。

3.2 The Proposed Framework

为解决上述问题，文章提出了一种端到端的评分框架，综合了两个图神经网络并结合图的节点表示随机知识蒸馏来训练深度异常检测器。该模型能够有效检测出这两种类型的异常图。

3.2.1 Overview of the Framework

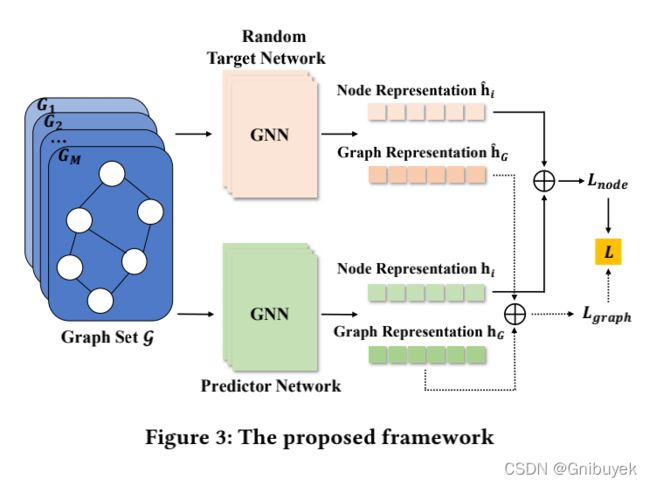
文章提出的框架同时提取每个图的图级和节点级表示，以学习全局和局部的图正常信息。它由两个完全相同结构的图神经网络（固定的随机初始化目标网络和预测网络）和两个蒸馏损失组成。通过训练预测网络来预测随机目标网络产生的图（节点）级表示以学习整体（细粒度）图的正常信息。 和  分别表示由预测网络和目标网络输出的图  的表示， 和  分别是两个网络生成的图 中节点  的表示。整体的目标函数可以表示为：

其中  是平衡图级和节点级损失函数重要性的参数， 和  分别是图级和节点级蒸馏损失函数。 是一个蒸馏函数，用于衡量两个特征表示之间的差异， 为图的数量。

整个框架训练阶段的总体流程如下：（1）首先随机初始化一个图网络  作为目标网络，并固定其权重参数  ，对于每个给定的图  ，它将为图  生成一个图级表示  和每个节点  一个节点级表示  ；（2）通过  对一个与  结构相同的预测网络  进行参数化训练，以预测目标网络的输出表示，也就是对于一个 图  ，生成图级表示  和节点级表示  ；（3）最终对于图 ，将 、、、 整合到损失函数  中，最小化损失函数以训练预测网络  。 

在评估阶段，给定图  的异常分数定义如下，其中  是预测网络的可学习参数：

3.2.2 Key Intuition 

图的图级和节点级表示是通过GNN来学习的，GNN具有捕捉图结构和语义信息的强大能力，在各种学习任务和应用中都得到了验证。框架中的联合随机蒸馏使得预测器网络的图表示和节点表示都尽可能接近于固定随机目标网络在正常图数据上的相应输出。这类似于提取图和节点随机表示中的不同模式（频繁或不频繁）。如果一个模式经常出现在随机表示空间中，那么这个模式就会被更好的提炼出来。比如当样本量较大时预测误差较小，否则预测误差较大。因此联合随机蒸馏从图表示和节点表示中学习这些规则性信息。对于给定的测试图  ，如果不符合图或节点级嵌入在训练图集  中规则行信息，其异常分数  会很大。

4 Joint Random Distillation of Graph and Node Representation

该框架实例化为GLocalKD方法，使用图卷积网络GCN学习节点和图的表示，联合蒸馏由两个基于均方误差的损失函数驱动。

4.1 Graph Neural Network Architecture

4.1.1 Random Target Network

 是一个具有固定随机初始化权重  的GCN， 是图  中的节点数量， 是节点表示的预定义维度大小。对于  中每个图 ，邻接矩阵  和特征矩阵 作为GCN的输入，使用  映射每个节点  到表示空间。 表示节点  在第  层的表示:

其中  是ReLU激活函数， 表示节点  的一阶邻居集合， 是对角度矩阵， ，，（ 是一个单位矩阵）， 在第0层的输入表示是其特征向量： 。因此节点  的输出随机节点表示可以写成：

其中  为  的层数。属性图的特征矩阵  由节点特征组成，对于没有节点属性特征的图，使用节点度作为特征构造简单的特征矩阵  。

然后，将READOUT操作应用到节点表示中以学习  的图级表示：

4.1.2 Predictor Network

预测器网络是一个用于预测目标网络输出表示的图网络，使用与目标网络完全相同的GCN结构，表示为： ， 为可学习权重参数。与目标网络类似，预测网络输出的节点  表示可描述为：

通过与  相同的READOUT操作，图表示通过下面公式计算：

因此随机目标网络  和预测网络  的唯一区别是  是随机初始化之后固定的，而  需要通过下面的全局和局部知识蒸馏来学习。

4.2 Glocal Regularity Distillation

通过最小化预测网络和目标网络产生的（图级和节点级）表示之间的距离，进一步执行全局局部正则化蒸馏。具体来说，图级和节点级蒸馏损失函数定义如下：

 

为了同时学习全局和局部图正则化信息，整合上述损失函数以优化：

4.3 Anomaly Detection of Using GLocalKD

通过联合全局局部随机蒸馏，预测器网络中学习的表示在图级和节点级捕获正则性信息。给定一个测试图样本  ，它的异常分数定义为在图和节点级表示的预测误差，表明在文章的异常评分中，局部异常和全局异常图同等重要：

5 Experiments and Results

5.1 Datasets

选择了16个公开的来自不同领域的真实世界数据集。表中前六个数据集为属性图，即每个节点具有一定的描述特征，其它都是简单的图。HSE，MMP，p53和PPAR-gamma是有真实异常图的数据，其余12个数据集将少数类视为异常，转换为异常检测任务。

5.2 Competing Methods

Two-step Methods：（iForest和LESINN）InfoGraph、WL、PK

End-to-end Methods：OCGCN

5.3 Implementation and Evaluation

GLocalKD的目标网络和预测器网络具有相同的结构，即三层GCN网络。隐层维度为512，输出层有256个神经单元。通过网格搜索选择学习率，取值范围为  。除HSE，MMP，p53和PPAR-gamma四个最大的数据集batch=2000，其余数据集batch=300.

评价指标：AUC、标准偏差（四个最大的数据集基于5此不同随机种子，其余5折交叉检验）

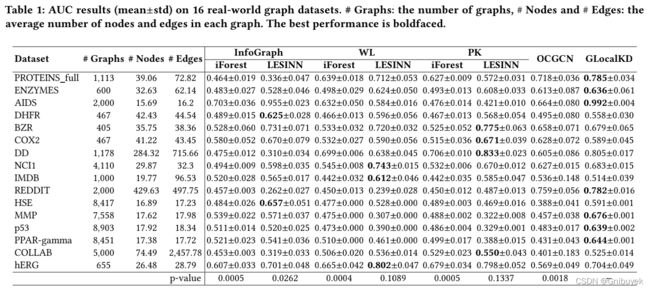
5.4 Comparison to State-of-the art Methods

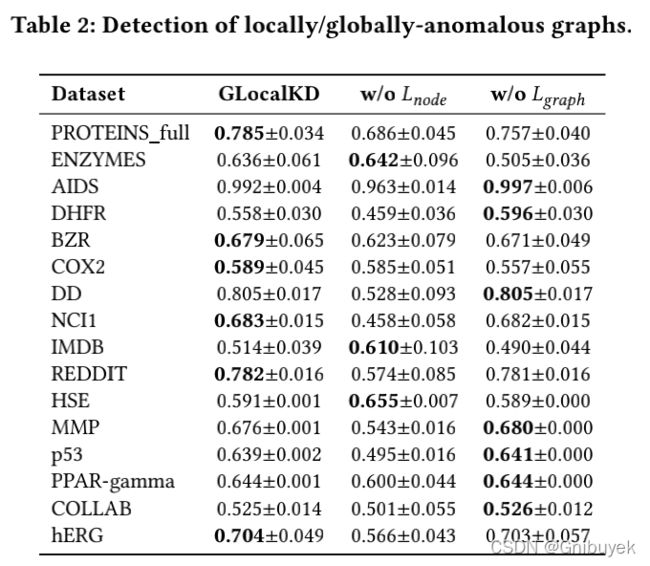
GLocalKD模型在七个数据集上表现最优，在DD和COLLAB等其他数据集上，本文提出的模型性能非常接近最佳对比方法。同时现有预测方法只能捕捉局部或全局信息，而GLocalKD可以同时学习局部和全局图的规律。如表2所示，如果只学习局部/全局图规律，则性能会大幅度下降。 

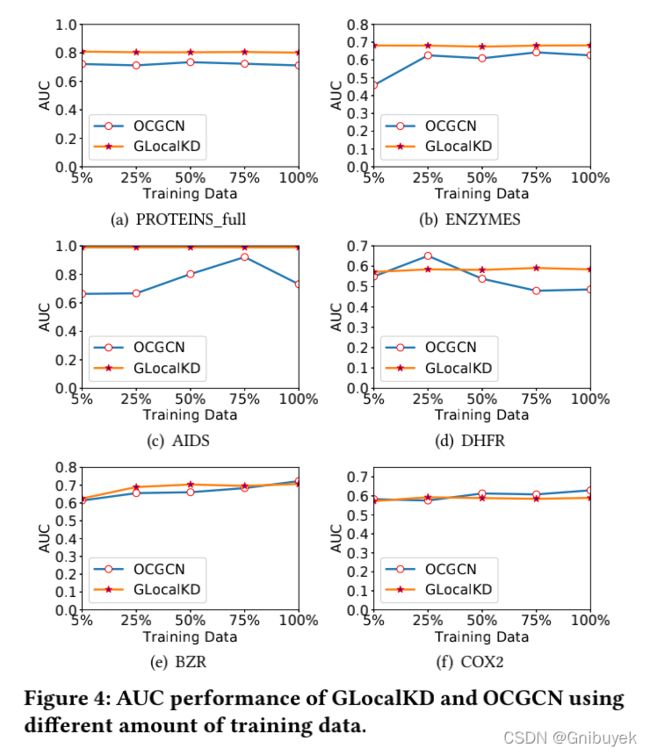
5.5 Sample Efficiency

分别测试使用5%、25%、50%、75%和100%的原始训练样本对模型训练，并在同一测试数据集上评估模型性能。比较结果表明GLocalKD可以在几乎所有的测试中保持同样良好的性能。

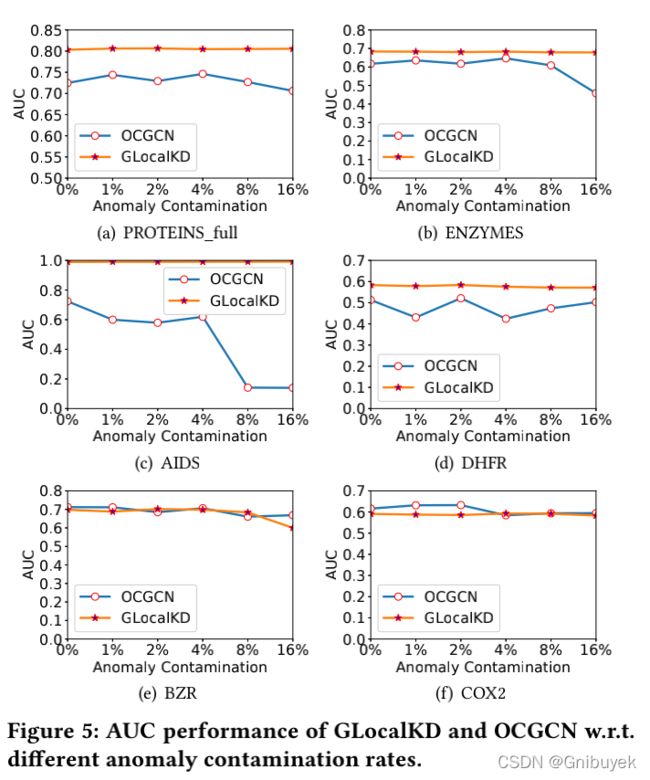
5.6 Robustness w.r.t. Anomaly Contamination

在实际应用中，收集的数据可能存在一些异常或数据噪声的污染，文章还研究了不同异常污染水平下模型的鲁棒性。实验结果表明，GLocalKD几乎不受污染的影响，在所有数据集上表现非常稳定，这主要是因为GLocalKD本质上是通过随机蒸馏来学习训练数据中各种类型的表示，只要异常表示在训练数据中出现的频率低于正常表示就可以检测出异常，而比较方法OCGCN的异常度量方法对异常污染较为敏感。

5.7 Sensitivity Test

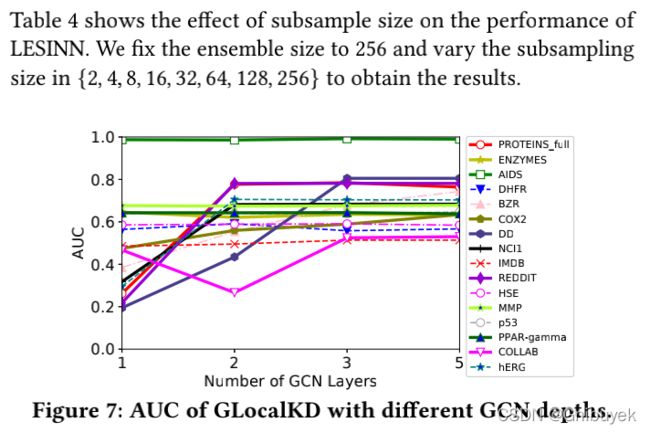
文章还测试表示维度和GCN深度对模型性能影响。在大多数数据集上，改变表示维度的大小，GLocalKD的性能始终保持稳定。此外在几乎所有的数据集上，随着GCN深度的增加，GLocalKD获得了更好的性能。当深度从3增加到5的时候，性能开始不再变化。此处使用网络深度为3，因为更深层的GCN并不能实现更好的性能，同时计算成本更高。

6 Conclusion

文章提出了一种新的检测异常图的框架GLocalKD。该方法也是第一个设计用来同时检测全局和局部图异常的模型。大量的实验表明，本文提出的方法性能较优，与现有的模型相比，它可以更有效地进行训练。同时，在训练数据中有很大的异常污染时，GLocalKD也能实现很好的性能。

7 Appendix

Implementation Details

Dataset	learning rate	batch	epochs
PROTEIN_full		300	150
ENZYMES		300	150