【推荐系统】02 协同过滤算法

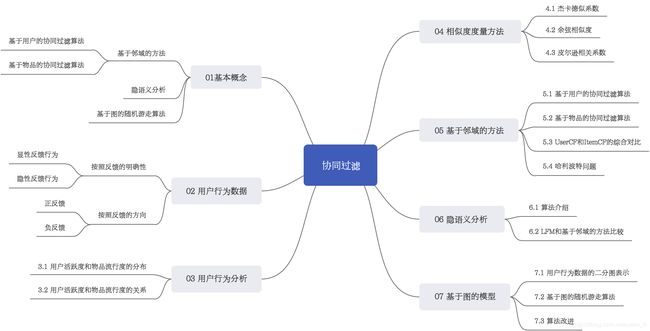
00 总览

01 基本概念

​ 协同过滤(Collaborative Filtering)是推荐系统中最经典、最常用的一类算法。所谓协同过滤算法，即一类基于用户行为分析的推荐算法。顾名思义可以解释为，用户可以齐心协力，通过不断与网站互动，是自己的推荐列表能够不断滤掉自己不感兴趣的物品，从而越来越满足自己的需求。

图1.1 协同过滤算法的常用方法

​ 其基本思想是根据用户之前的喜好以及其他兴趣相近的用户的选择来给用户推荐物品。一般仅仅基于用户的行为数据，而不依赖于物品和用户信息。目前比较广泛的协同过滤算法是基于近邻的方法，而这种方法主要有下面两种算法：

• 基于用户的协同过滤算法(UserCF)：给用户推荐和他兴趣相似的其他用户喜欢的产品；
• 基于物品的协同过滤算法(ItemCF)：给用户推荐和他之前喜欢的物品相似的物品。

​ 无论是使用UserCF还是ItemCF算法，非常重要的步骤之一就是需要计算用户与用户或者物品与物品之间的相似度。当然除了这两种方法以外还有隐语义分析以及基于图的随机游走算法等基于用户行为数据的推荐算法，这些内容都将在后续内容中展开。

02 用户行为数据

图2.1 网站数据收集过程

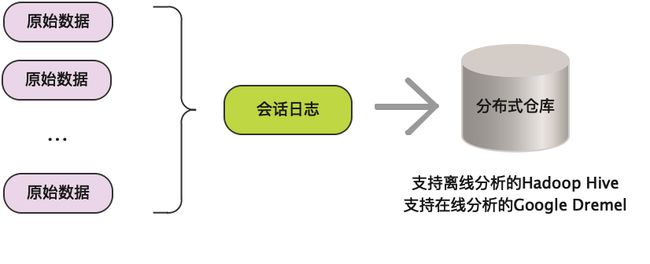
​ 用户行为数据在网站上最简单的存在形式就是日志。网站在运行过程中都会产生大量的原始数据(raw log)，并将其存储在文件系统中。其基本过程如上图所示。这些日志记录了用户的各种行为，如在电子商务网站中的网页浏览、购买、点击、评分和评论等。

图2.2 用户行为分类

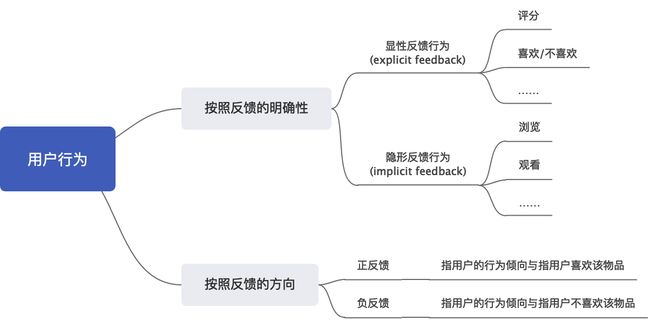
​ 用户行为分为显性反馈行为和隐形反馈行为。其中显性反馈行为包括用户明确表示对物品喜好的行为。隐形反馈行为是指那些不能明确反映用户爱好的行为。

表2.1 显性反馈数据和隐形反馈数据的对比

	显性反馈数据	隐形反馈数据
用户兴趣	明确	不明确
数量	较少	庞大
存储	数据库	分布式文件系统
实时读取	实时	有延迟
正负反馈	都有	只有正反馈

​ 互联网中的用户行为分为很多种，表2.2给出了一种表示方法，它将一个用户行为表示为6部分。

表2.2 用户行为统一表示

标识	说明
User id	产生行为的用户的唯一标识
item id	产生行为的对象的唯一标识
behavior type	行为的种类（浏览，购买等）
context	产生行为的上下文，包括时间地点等
behavior weight	行为的权重（比如观看时长，评分等）
behavior content	行为的内容（如评论文本、打的标签等）

​ 很多时候我们并不使用统一结构表示所有行为，而是针对不同的行为给出不同的表示。当然，有一些信息我们是不能忽略的，比如行为用户和对象。一般来说，比较有代表性的数据集分为以下几种：

图2.3 数据集分类及示例

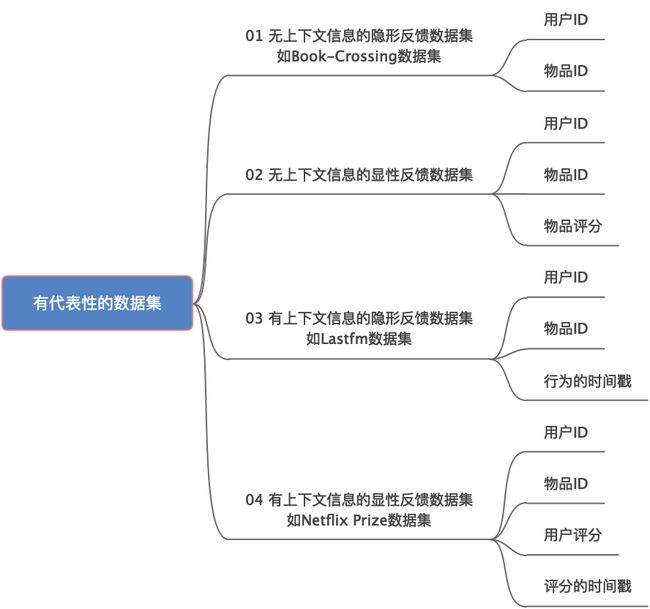
​ 典型的数据集除了上图中所示的几类，还有一些比较常见的如Netflix、MovieLens、Delicious 和 CiteULike等数据集。

03 用户行为分析

​ 利用用户行为数据进行算法推荐之前，需要对用户行为数据进行分析，了解其蕴含的一般规律，这样才能对于算法的设计起到指导作用。本节主要介绍用户行为数据中的一般普遍规律

3.1 用户活跃度和物品流行度的分布

​ 互联网上的很多数据都满足Power Law的分布，这个分布也被成为长尾分布。为了说明用户行为的长尾分布，作者选择了Delicious和CiteULike数据集一个月的原始数据进行了分析。
$$f\left(x\right)=\alpha x^k$$
​ 无论$f(x)$表示为对$x$个物品产生过行为的用户数还是表示为被$x$个用户产生过行为的物品数，都将会满足上述公式。

3.2 用户活跃度和物品流行度的关系

04 相似度度量方法

4.1 杰卡德(Jaccard)相似系数

​ 这个系数是两个集合的相似度一种指标。两个用户$u$和$v$交互商品交集的数量占这两个用户交互商品并集的数量的比例，称为这两个集合的杰卡德相似系数，用符号$si{m}_{uv}$表示，其中$N(u),N(v)$分别表示用户$u$和用户$v$交互商品的集合。
$$si{m}_{uv}=\frac{\left|N\left(u\right)\cap N\left(v\right)\right|}{\sqrt{\left|N\left(u\right)\cup N\left(v\right)\right|}}\text{\hspace{1em}(1)}$$
​ 由于杰卡德相似系数一般无法反映具体用户的评分喜好信息，所以常用来评估用户是否会对某商品打分，而不是预估用户会对商品打多少分。

4.2 余弦相似度

​ 余弦相似度衡量了两个向量的夹角，夹角越小越相似，相比于Jaccard相似度，该公式的分母与之有差异。
$$si{m}_{uv}=\frac{\left|N\left(u\right)\cap N\left(v\right)\right|}{\sqrt{\left|N\left(u\right)\cup N\left(v\right)\right|}}\text{\hspace{1em}(2)}$$

4.3 皮尔逊相关系数

​ 皮尔逊相关系数与余弦相似度比较类似，
$$si{m}_{uv}=\frac{{\sum }_i{r}_{ui}{r}_{vi}}{\sqrt{{\sum }_i{r}_{ui}^2}\sqrt{{\sum }_i{r}_{vi}^2}}\text{\hspace{1em}(3)}$$
其中$r_{ui}$和$r_{vi}$分别代表用户u和用户v对商品i是否有交互。

05 基于邻域的算法

​ 基于邻域的算法是推荐系统中最基本的算法，该算法主要分为两大类：基于用户的协同过滤算法和基于物品的协同过滤算法。

5.1 基于用户的协同过滤算法

1. 算法介绍

​ 主要包括两个步骤：

（1）找到和目标用户兴趣相似的用户集合

（2）找到这个集合中的用户喜欢的，而目标用户不知道的物品推荐给该目标用户

​ 步骤（1）中我们可以通过Jaccard公式或余弦相似度^附1简单地计算出两个用户的兴趣相似度。

2. 算法改进方法

5.2 基于物品的协同过滤算法

​ 基于物品的协同过滤算法是目前业界用的最多的推荐算法。其中包括亚马逊、Netflix、Hulu、YouTube。

1. 算法介绍

​ 主要包括两个步骤：

（1）计算物品之间的相似度

（2）根据物品的相似度和用户的历史行为给用户生成推荐列表

​ 最简单的方法我们可以用下面的方法定义物品的相似度：
$$w_{ij}=\frac{\left|N(i)|\cap N(j)\right|}{\left|N(i)\right|}\text{\hspace{1em}(5.1)}$$
这里$\left|N(i)\right|$是喜欢物品$i$的用户数，而分子表示的是同时喜欢物品$i,j$的用户数。

2. 算法改进

• 热门物品的对物品相似度的影响

​ 这个公式看起来非常合理，不过如果一个物品非常热门，那么它的$W_{ij}$就会很大，它和所有的物品都会具有很大的相似度。为了避免这种情况，我们可以改用下面的公式：
$$w_{ij}=\frac{\left|N(i)\cap N(j)\right|}{\sqrt{\left|N(i)\right|\left|N(j)\right|}}\text{\hspace{1em}(5.2)}$$

• 用户活跃度度物品相似度的影响

​ 基于物品的协同过滤主要是考虑它们有共同的感兴趣用户，但是是否每个用户的对于物品的相似度都相同呢？例如一个在书店老板一次购买3000本书和一个文艺青年一次购买自己喜欢的30本书。书店老板虽然活跃，但是并非出自兴趣，所以这个用户对于物品相似度的贡献远远小于文艺青年对于物品相似度的贡献。
​ 对于书店老板这种过于活跃的用户，一般直接忽略他的兴趣列表以避免相似度矩阵过于稠密。而为了考虑到用户活跃度对于物品相似度的影响，John S.Breese在论文中提出了IUF(Inverse User Frequence)，即用户活跃度对数的倒数修正物品相似度
$$\begin{gathered} w_{ij}=\frac{{\sum }_{u\in N(i)\cap N(j)}\frac{1}{\log (1+|N(u)|)}}{\sqrt{\left|N(i)\right|\left|N(j)\right|}} \\ \text{\hspace{1em}(5.3)} \end{gathered}$$

• 物品相似度归一化

​ Karypis在研究中发现如果将ItemCF的相似度矩阵按最大值归一化，可以提高推荐的准确率。归一化之后的相似度矩阵计算：
$$w_{ij}^{\prime }=\frac{w_{ij}}{{\max }_j{w}_{ij}}\text{\hspace{1em}(5.4)}$$
其实归一化不仅可以增加推荐的准确度，同时还可以提高推荐的覆盖率和多样性。

5.3 UserCF和ItemCF的综合比较

​ UserCF的推荐结果更社会化，反映了用户所在的小型兴趣群体中的热门程度，而ItemCF的推荐更加个性化，反映了用户自己的兴趣传承。从技术角度来讲，UserCF需要网站维护一个用户的相似度矩阵，而ItermCF则需要维护一个物品直接的相似度矩阵。从存储角度来讲，如果用户很多，则维护用户兴趣相似度矩阵需要很大的空间，同理如果物品很多，则需要维护物品相似度矩阵代价较大。

表5.1 UserCF和ItemCD综合比较

​ 值得指出的是，离线实验的性能在选择推荐算法时并不起决定性作用。首先，应该满足产品需求。比如如果需要提供推荐解释，则可能只能选择ItemCF算法；其次，需要看实现代价。比如用户太多，很难计算用户的相似度矩阵，则这时候可能不得不抛弃UserCF算法；最后，离线指标与点击率不一定成正比。书中展现的都是最原始的UserCF和ItemCF，这两种算法都可以进行各种各样的改进，一般来说，这两种算法经过优化后能得到比较近似的离线性能。

5.4 哈利波特问题

​ 亚马逊的研究人员在设计ItemCF算法之处发现一个问题，就是很多书都和《哈利波特》这本书有关，也就是说，购买任何一本书的人似乎都会购买《哈利波特》。这一问题可以通过上面的公式（4.2）得到缓解，但是热门的$j$仍然会获得比较大的相似度。
​ 这个问题也有几个可以解决的方案，最简单的就是加大对热门物品的惩罚，比如采用如下公式
$$w_{ij}=\frac{\left|N(i)\cap N(j)\right|}{{\left|N(i)\right|}^{1-\alpha }{\left|N(j)\right|}^{\alpha }}\text{\hspace{1em}(5.5)}$$
其中$\alpha \in [0.5,1]$。通过提高$\alpha$，就可以加大对热门的$j$的惩罚。如果$\alpha =0.5$就又是标准的ItemCF算法，从离线实验可以得到，只有$\alpha =0.5$时才会有最高的准确率和召回率，其他情况都会导致其降低。因此，这种方法可以在适当牺牲准确率和召回率的情况下显著提高结果的覆盖率和新颖性。
不过，上述的方法还是不能彻底解决哈利波特问题，而且每一个用户一般都会在不同的领域喜欢一种物品，即往往会导致两个不同领域的热门物品之间往往具有比较高的相似度。这个时候，仅仅通过用户行为数据是不能解决这个问题的，所以只能依靠引入物品的内容数据解决这个问题，比如在不同领域的物品降低权重等。

06 隐语义分析

​ 该算法最早在文本挖掘领域被提出，用于找到文本的隐含语义。相关的名词有LSI、pLSA、LDA和Topic Model。本节将主要对隐含语义模型在Top-N推荐中的应用进行详细介绍。

6.1 基础算法

​
该算法最早在文本挖掘领域被提出，用于找到文本的隐含语义。相关的名词有LSI、pLSA、LDA和Topic Model。本节将主要对隐含语义模型在Top-N推荐中的应用进行详细介绍。这种算法可以看作是UserCF和ItemCF的一种延伸，即把用户相似性和物品的相似度通过一个叫隐向量的方式进行表达。

6.1 基础算法

​ 核心思想：通过隐含特征(latent factor)联系用户兴趣和物品。隐语义分析从诞生到今天已经产生了许多著名的模型和方法，其中包括pLSA、LDA、隐含类别模型(latent class model)、隐含主题模型(latent topic model)、矩阵分解(Matrix factorization)。这些技术本质上都是相通的。

​ LFM通过如下公式计算用户u对物品的兴趣：
$$Preference(u,i)=r_{ui}=p_u^T{q}_i=\sum _{f=1}^F{p}_{u,k}{q}_{i,k}\text{\hspace{1em}(6.1)}$$
这个公式中的$p_{u,k}$和$q_{i,k}$是模型的参数，其中$p_{u,k}$度量了用户u的兴趣和第$k$个隐类的关系，而$q_{i,k}$度量了第$k$个隐类和物品$i$的关系。要计算这两个参数，需要一个训练集，对于每个用户u，训练集里都包含了用户u喜欢的物品和不感兴趣的物品，通过学习这个训练集，我们就可以得到上面的模型参数。

​ 推荐系统的用户行为分为显性反馈和隐形反馈。LFM在显性反馈数据上解决评分预测问题并达到了很好的精度。不过本章主要讨论的是隐性反馈数据集，这种数据集的特点就是只有正样本，而没有负样本。那么，在隐性反馈数据集上应用LFM解决TopN推荐的第一个关键问题就是如何给每个用户生成负样本。通过2011年的KDD Cup的Yahoo! Music推荐系统比赛，我们发现对负样本采样应该遵循以下原则：

• 对于每个用户，要保证正负样本的平衡（数目相似）；
• 对每个用户采负样本是，要选取那些很热门，而用户却没有行为的商品。

在LFM中，重要的参数有四个：①隐特征的个数F；②学习速率alpha；③正则化参数lambda；④负/正样本比例ratio。

​ 通过实验发现，ratio参数对LFM的性能影响最大。因此通过固定$F=0,\alpha =0.02,lambda=0.01$，研究发现：随着负样本数目的增加，LFM的准确率和召回率都有明显的提高。不过当$ratio>10$以后，准确率和召回率基本就稳定了。同时，对着负样本的数目的不断增加，覆盖率不断地降低，而推荐结果的流行度不断增加，说明ratio参数控制了推荐算法发掘长尾的能力。通过对比比较可以发现，在MovieLens数据集上LFM的结果在所有指标上都优于UserCF和ItemCF。当数据非常稀疏时，LFM的性能会明显下降，甚至不如UserCF和ItemCF的性能。

6.2 矩阵分解算法的原理

​ 一般情况下，我们无法得到公式中的$p_{u,k}$和$q_{i,k}$，而只有一个评分矩阵，这种矩阵非常的稀疏，如果想直接基于用户相似性和物品相似性去填充这个矩阵并不容易，并且容易出现长尾分布问题。所以考虑用矩阵分解模型解决这个问题。矩阵分解模型其实就是想办法基于这个评分矩阵去找到对应的$p_{u,k}$和$q_{i,k}$，也就是用户兴趣与物品的隐向量表达，然后就把这个评分矩阵分解成了$p_{u,k}$和$q_{i,k}$两个矩阵乘积的形式，这时候就可以基于两个矩阵去预测某个用户对某个物品的评分了。

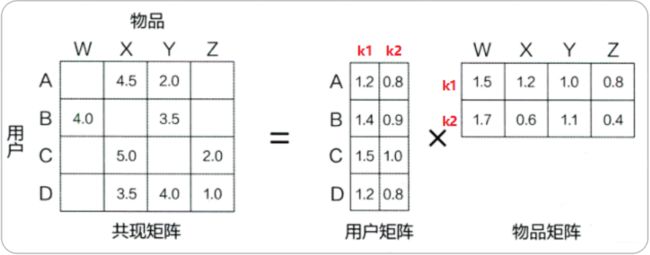
​ 在矩阵分解的算法框架下，我们可以通过分解协同过滤的共现矩阵来得到用户和物品的隐向量。如下图6.1所示

图6.1 LFM中的矩阵分解

6.3 矩阵分解法的求解

​ 矩阵分解最为为常用的方法是特征值分解(EVD)或者奇异值分解(SVD)，关于这两个的具体原理可以参考下面的参考内容。但是这两个方法在这里都不适用。EVD要求矩阵是方阵，而传统的SVD分解，要求矩阵是稠密的。

6.4 LFM和基于邻域的方法的比较

​ LFM是一种基于机器学习的方法，具有比较好的理论基础。这个方法有UserCF相比，各有优缺点。其对比如下表5.1所示。

表6.1 LFM与基于邻域方法的比较

07 基于图的模型

​ 用户行为很容易用二分图表示，因此很多图的算法都可以应用到推荐系统中来

7.1 用户行为数据的二分图表示

​ 基于图的模型(graph-based model)是推荐系统的重要内容。研究图模型之前，我们需要将用户行为数据表示成图的形式。本文中所讨论的用户行为数据是由一系列二元组组成的，其中每个二元组$(u,i)$表示用户$u$对物品i产生过行为。这种数据集可以比较容易的用一个二分图表示。

​ 令$G(V,E)$表示用户物品二分图，其中$V=V_u\cup V_I$由用户顶点集合$V_U$ 和物品的顶点集合$V_I$组成。如图6.1是一个简单的用户物品二分图模型，其中圆形节点代表用户，方形节点代表物品，方形节点和圆形节点之间的连线表示用户对物品产生过行为。

图7.1 用户物品二分图模型

7.2 基于图的推荐算法

​ 如果将个性化算法放在二分图模型上，那么给用户u推荐物品的任务就可以转化为度量用户顶点$V_U$和与$V_U$没有边直接相连的物品节点在图上的相关性，相关性越高的物品在推荐列表中的权重就越高。
​ 度量图中两个顶点之间相关性的方法有很多，但一般来说，图中顶点的相关性主要取决于3个因素：

• 两个顶点之间的路径数；（越多相关性越高）
• 两个顶点之间路径的长度；（路径长度比较短）
• 两个顶点之间的路径经过的顶点。（路径不会经过出度比较大的顶点）

​ 基于以上三个主要因素，研究人员设计出了很多计算图中顶点之间的相关性方法，本节将介绍一种基于随机游走的PersonlRank算法。
​ 假设要给用户u进行个性化推荐，可以从用户u对应的节点V_u开始在用户物品二分图上进行随机游走。游走到任何一个节点时，首先按照概率$\alpha$决定是继续游走还是停止到这次游走并从V_u节点开始重新游走。如果决定继续游走，那么就从当前节点指向的节点中按照均匀分布随机选择一个节点作为游走下次经过的节点。这样，经过多次随机游走后，每个物品节点被访问的概率会收敛到一个数。最终的推荐列表中的物品的权重就是物品节点的访问概率。描述公式如下
$$PR(v)=\{\begin{array}{c}\alpha {\sum }_{v^{\prime }\in in(v)}\frac{PR(v^{\prime })}{|out(v^{\prime })|}(v\ne v_u)\\ (1-alpha)+\alpha {\sum }_{v^{\prime }\in in(v)}\frac{PR(v^{\prime })}{|out(v^{\prime })|}(v=v_u)\end{array}\text{\hspace{1em}(7.1)}$$
​ 虽然PersonalRank算法可以通过随机游走进行比较好的理论解释，但是该算法在时间复杂度上有明显的缺点。因为在为每个用户进行推荐时，都需要在整个用户物品二分图上进行迭代，直到整个图上的每个顶点的PR值收敛。这一过程的时间复杂度相当的高，不仅无法提供实时推荐，甚至在离线生成推荐结果也很耗时。

7.3 算法改进

​ 为了解决PersonalRank每次都需要在全图迭代并因此造成时间复杂度很高的问题，这里给出两种解决方案。① 减少迭代次数，在收敛之前就停止。这样虽然在会影响最终精度，但是一般来说影响不是很大。② 从矩阵论出发，重新设计算法。
​ 从矩阵的角度出发，令M为用户物品二分图的转移概率矩阵，即：
$$M(u,v^{\prime })=\frac{1}{|out(v)|}\text{\hspace{1em}(7.2)}$$
这样迭代公式可以转化为：
$$r=(1-\alpha )r_0+\alpha M^{T}r\text{\hspace{1em}(7.3)}$$
可以解出：
$$r=(1-\alpha )(1-\alpha M^T{)}^{-1}{r}_0\text{\hspace{1em}(7.4)}$$
因此，只需要计算一次$(1-\alpha M^T{)}^{-1}$，这里的$1-\alpha M^T$是稀疏矩阵，可以参考矩阵有关的书使用稀疏矩阵的快速求逆。

---

参考目录：

1. 项亮《推荐系统实践》