Learning to Rank(LTR, Pointwise,Pairwise,Listwise, NDCG, RankNet, ranklib)
LTR介绍以及排序算法与工具使用
LTR简介
排序学习
- 推荐系统,搜索,广告的核心算法之一(LTR不仅被应用到搜索中,也应用到所有与排序相关的各种需求中)
- Ranking模型,基于相关度和基于重要性进行排序
- 基于相关度的Ranking,有监督的机器学习过程,对每一个给定的Query-doc对,抽取特征,通过日志挖掘或者人工标注的方法获得真实数据标注。然后通过排序模型,使得输入能够和实际的数据相似。
排序学习场景:
- 推荐系统,基于历史行为的“猜你喜欢”
- 搜索排序,基于某Query进行的结果排序,期望用户选中的在排序结果中是靠前的 => 有意识的被动推荐
- 排序结果都很重要,猜用户想要点击或者booking的item就在结果列表前面
- 排序学习是个性化结果,用于搜索列表、推荐列表、广告等场景
排序模型按照样本生成方法和损失函数的不同,可以划分成Pointwise, Pairwise, Listwise三类方法:
- Pointwise排序学习(单点法):
将训练样本转换为多分类问题(样本特征-类别标记)或者回归问题(样本特征-连续值)
只考虑单个样本的好坏,没有考虑样本之间的顺序 - Pairewise排序学习(配对法):
比较流行的LTR学习方法,将排序问题转换为二元分类问题
接收到用户査询后,返回相关文档列表,确定文档之间的先后顺序关系(多个pair的排序问题),只考虑了两个文档的相对顺序,没有考虑文档在搜索列表中的位置。 - Listwise排序学习(列表法):
它是将每个Query对应的所有搜索结果列表作为一个训练样例
根据训练样例训练得到最优评分函数F,对应新的查询,评分F对每个文档打分,然后根据得分由高到低排序,即为最终的排序结果
排序模型按照结构划分,可以分为线性排序模型、树模型、深度学习模型:
从早期的线性模型LR,到引入自动二阶交叉特征的FM和FFM,到非线性树模型GBDT和GBDT+LR,到最近全面迁移至大规模深度学习排序模型。
- 线性排序模型:LR
- 树模型:GBDT,GBDT+LR, LambdaMART
- 深度学习模型: DeepFM,Wide&Deep, ListNet, AdaRank,SoftRank,LambdaRank等
Pointwise, Pairwise, Listwise三类方法
Pointwise排序学习中的基本LR模型:
- 逻辑回归模型(Logistic Regression,LR)
- 在实际信息流中,人对feed最简单就是两种行为,点击或者不点击,label分别标记为1和0
- LR用于建模point-wise方式的数据,这种模型直接对标注好的point-wise数据,学习 P(y|x)或直接回归预测y
- LR模型损失函数: J ( θ ) = − 1 N ∑ i = 1 w i ⋅ ( y i log ( σ θ ( x i ) ) + ( 1 − y i ) log ( 1 − σ θ ( x i ) ) ) J\left( \theta \right) = - \frac{1}{N}\sum\limits_{i = 1} {{w_i} \cdot \left( {{y_i}\log \left( {{\sigma _\theta }({x_i})} \right) + \left( {1 - {y_i}} \right)\log \left( {1 - {\sigma _\theta }({x_i})} \right)} \right)} J(θ)=−N1i=1∑wi⋅(yilog(σθ(xi))+(1−yi)log(1−σθ(xi)))
wi为样本权重,yi为样本label σ θ ( x i ) = 1 1 + e − ( θ x + b ) {\sigma _\theta }({x_i}) = \frac{1}{{1 + {e^{ - \left( {\theta x + b} \right)}}}} σθ(xi)=1+e−(θx+b)1
LR模型可解释性好,方便问题定位和查找,通过特征权重可以解释feed排序的得分,可以人工分析和判断模型参数是否合理。同时我们也可以用GBDT+LR进行预测,使用GBDT构造新特征,然后用LR将GBDT构造好的特征进行训练,因为对特征进行了组合,相当于用GBDT进行特征工程筛选特征组合后用LR进行预测后的效果一般要比单用LR好不少。
Pointwise排序学习(单点法)总结:
- 将文档转化为特征向量,每个文档都是独立的
- 对于某一个query,它将每个doc分别判断与这个query的相关程度
- 将docs排序问题转化为了分类(比如相关、不相关)或回归问题(相关程度越大,回归函数的值越大)
- 从训练数据中学习到的分类或者回归函数对doc打分,打分结果即是搜索结果,CTR可以采用Pointwise方式进行学习,对每一个候选item给出一个评分,基于评分进行排序
- 仅仅考虑了query和doc之间的关系,而没有考虑排序列表中docs之间的关系
- 主要算法:转换为回归问题,使用LR,GBDT,Prank, McRank
Pairewise排序学习(配对法)总结:
- 比较流行的LTR学习方法,将排序问题转换为二元分类问题
- 接收到用户査询后,返回相关文档列表,确定文档之间的先后顺序关系(多个pair的排序问题)
- 对于同一查询的相关文档集中,对任何两个不同label的文档,都可以得到一个训练实例(di,dj),如果di>dj则赋值+1,反之-1
- 没有考虑文档出现在搜索列表中的位置,排在搜索结果前面的文档更为重要,如果靠前的文档出现判断错误,代价会很高
- 主要算法:SVM Rank,RankBoost(2003),RankNet(2007)
Listwise排序学习(列表法)总结:
- 它是将每个Query对应的所有搜索结果列表作为一个训练样例
- 根据训练样例训练得到最优评分函数F,对应新的查询,评分F对每个文档打分,然后根据得分由高到低排序,即为最终的排序结果
- 直接考虑整体序列,针对Ranking评价指标(比如MAP, NDCG)进行优化
- 主要算法:ListNet, AdaRank,SoftRank,LambdaRank, LambdaMART等
LambdaMART是对RankNet和LambdaRank的改进,在 Yahoo Learning to Rank Challenge比赛中的冠军模型
评测指标
MAP
Mean Average Precision,平均准确率
- 对于每个真实相关的文档,考虑其在模型排序结果中的位置 P,统计该位置之前的文档集合的分类准确率,取所有这些准确率的平均值。
P @ k ( π , l ) = ∑ t ≤ k I { l π − 1 ( t ) = 1 } k P@k\left( {\pi ,l} \right) = \frac{{\sum\limits_{t \le k} {{I_{\{ {l_{{\pi ^{ - 1}}(t)}} = 1\} }}} }}{k} P@k(π,l)=kt≤k∑I{lπ−1(t)=1}
π \pi π代表documents list,即推送结果。 是指示函数
=> 前k个documents中,标签为1的documents个数与k的比值
A P ( π , l ) = 1 m 1 ∑ k = 1 m P @ k ⋅ I { l π − 1 ( t ) = 1 } AP\left( {\pi ,l} \right) = \frac{1}{{{m_1}}}\sum\limits_{k = 1}^m {P@k \cdot } {I_{\{ {l_{{\pi ^{ - 1}}(t)}} = 1\} }} AP(π,l)=m11k=1∑mP@k⋅I{lπ−1(t)=1}
m1代表查询出的真实标签为1的doc数量(label=1),m代表模型找出的前m个doc
假设有两个主题:主题1有4个相关网页,主题2有5个相关网页。
某系统对于主题1检索出4个相关网页,其rank分别为1, 2, 4, 7
对于主题2检索出3个相关网页,其rank分别为1,3,5
对于主题1,平均准确率为(1/1+2/2+3/4+4/7)/4=0.83
对于主题2,平均准确率为(1/1+2/3+3/5+0+0)/5=0.45
所以MAP=(0.83+0.45)/2=0.64
NDCG
CG(cumulative gain):
- 累计增益,只考虑到了相关性,没有考虑到位置的因素 C G p = ∑ i = 1 p r e l i C{G_p} = \sum\limits_{i = 1}^p {re{l_i}} CGp=i=1∑preli
- 比如针对Query,理想结果是c1,c2,c3,实际结果为c3,c2,c1,CG不变
DCG(Discounted CG)
折损累计增益,在每一个CG的结果上除以一个折损值,为了让排名靠前的结果能影响最后的结果
排序越往后价值越低。到第i个位置的时候,价值是 1/log2(i+1),那么第i个结果产生的效益就是 reli * 1/log2(i+1),所以
D C G p = ∑ i = 1 p r e l i log 2 ( i + 1 ) DC{G_p} = \sum\limits_{i = 1}^p {\frac{{re{l_i}}}{{{{\log }_2}(i + 1)}}} DCGp=i=1∑plog2(i+1)reli
IDCG(ideal DCG)
理想情况下最大的DCG值:
I D C G p = ∑ i = 1 ∣ R E L ∣ r e l i log 2 ( i + 1 ) IDC{G_p} = \sum\limits_{i = 1}^{\left| {REL} \right|} {\frac{{re{l_i}}}{{{{\log }_2}(i + 1)}}} IDCGp=i=1∑∣REL∣log2(i+1)reli
|REL| 表示,结果按照相关性从大到小的顺序排序,取前p个结果组成的集合。也就是按照最优的方式对结果进行排序
NDCG(Normalized DCG)
归一化贴现累积收益,综合考虑模型排序结果和真实序列之间的关系,最终使用的排序指标
DCG是一个累加的值,没法针对两个不同的搜索结果进行比较,需要归一化处理
N D C G p = D C G p I D C G p NDC{G_p} = \frac{{DC{G_p}}}{{IDC{G_p}}} NDCGp=IDCGpDCGp
NDCG:
假设搜索回来的6个结果,其相关性分数(REL)分别是 3、2、3、0、1、2
累计增益 CG=3+2+3+0+1+2,只是对相关的分数进行了一个关联的打分,并没有召回的所在位置对排序结果评分对影响
计算DCG

DCG = 3+1.26+1.5+0+0.38+0.71 = 6.86
计算iDCG(理想情况下最大的DCG值)
假设实际召回了8个物品,还有两个结果,第7个相关性为3,第8个相关性为0。那么在理想情况下的相关性分数排序应该是:3、3、3、2、2、1、0、0。计算IDCG@6:
iDCG=3+1.89+1.5+0.86+0.77+0.35 = 8.37

所以最终的 NDCG@6 = 6.86/8.37 = 81.96%
MRR:
- 平均倒数排名,Mean Reciprocal Rank
- 把相关文档在结果中的排序倒数作为准确度,然后再取平均
- 比如3次Query,第一次Query,查询结果将正确结果排名 rank 为 3,则其 Reciprocal Rank 为 1/3,对于第二个 Query,查询结果将正确结果排名 rank 为 2,则其 Reciprocal Rank 为 1/2,对于第三个 Query,查询结果将正确结果排名 rank 为 1,则其 Reciprocal Rank 为 1,则 MRR = (1/3 + 1/2 + 1)/3 = 11/18 = 0.61
- 优点是计算简单,不足在于仅仅考虑了相关性最强的文档所在的位置带来的损失
排序算法
三种算法:RankNet,LambdaRank和LambdaMART,在Yahoo!Learning To Rank Challenge等比赛中表现出很好的排序效果
- RankNet是基于神经网络的排序算法
- 在RankNet的基础上加入了lambda梯度 => LambdaRank
- lambda梯度和MART(GBDT也称为MART,梯度提升树)结合 => LambdaMart
RankNet排序算法
RankNet:
-
目标就是对所有query,都能对doc结果按照相关性进行排序
-
例如搜索页面返回了10条相关结果,人们的浏览顺序是从上到下的,因此排在上面的要比下面的相关
-
RankNet是基于神经网络的排序学习方法,依赖于每个文档对,定义了一个基于概率的损失函数,运用神经网络和梯度下降法试图最小化一个交叉熵损失函数,终极目标是得到一个带参数的得分函数: s = f ( x ; w ) s = f\left( {x;w} \right) s=f(x;w)
-
根据这个函数,我们就可以求得 s i = f ( x i ; w ) s j = f ( x j ; w ) \begin{array}{l} {s_i} = f\left( {{x_i};w} \right)\\ {s_j} = f\left( {{x_j};w} \right) \end{array} si=f(xi;w)sj=f(xj;w)
-
将输入query的特征向量x∈Rn映射为一个实数f(x)∈R
-
采用pairwise的方法进行模型训练,对于给定query下的两个文档Ui和Uj,其特征向量分别为xi和xj,经过RankNet进行前向计算得到对应的分数为Si=f(xi)和Sj=f(xj)。用Ui⊳Uj表示Ui比Uj排序更靠前(如对某个query来说,Ui被标记为“good”,Uj被标记为“bad”)
得到这个pair的偏序概率:
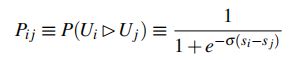
表示Ui应该比Uj排序更靠前的概率,Si-Sj为两两文档打分的差 -
这个概率实际上就是深度学习中经常使用的sigmoid函数,参数σ决定sigmoid函数的形状。对于特定的query,定义Sij∈{0,±1}为文档i和文档j被标记的标签之间的关联,即

P i j ‾ = 1 2 ( 1 + S i j ) \overline {{P_{ij}}} = \frac{1}{2}\left( {1 + {S_{ij}}} \right) Pij=21(1+Sij)表示Ui应该比Uj排序更靠前的真实后验概率
用交叉熵定义优化目标的损失函数:
C = − P i j ‾ log P i j − ( 1 − P i j ‾ ) log ( 1 − P i j ) C = - \overline {{P_{ij}}} \log {P_{ij}} - \left( {1 - \overline {{P_{ij}}} } \right)\log \left( {1 - {P_{ij}}} \right) C=−PijlogPij−(1−Pij)log(1−Pij) P i j {P_{ij}} Pij表示模型预估的概率
C = − P i j ‾ log P i j − ( 1 − P i j ‾ ) log ( 1 − P i j ) C = - \overline {{P_{ij}}} \log {P_{ij}} - \left( {1 - \overline {{P_{ij}}} } \right)\log \left( {1 - {P_{ij}}} \right) C=−PijlogPij−(1−Pij)log(1−Pij)
P i j ‾ = 1 2 ( 1 + S i j ) \overline {{P_{ij}}} = \frac{1}{2}\left( {1 + {S_{ij}}} \right) Pij=21(1+Sij)
带入后求得:
C i j = − 1 2 ( 1 + S i j ) log 1 1 + e − σ ( s i − s j ) − 1 2 ( 1 − S i j ) log e − σ ( s i − s j ) 1 + e − σ ( s i − s j ) = − 1 2 ( 1 + S i j ) log 1 1 + e − σ ( s i − s j ) − 1 2 ( 1 − S i j ) [ − σ ( s i − s j ) + log 1 1 + e − σ ( s i − s j ) ] = 1 2 ( 1 − S i j ) σ ( s i − s j ) + log ( 1 + e − σ ( s i − s j ) ) \begin{array}{l} {C_{ij}} = - \frac{1}{2}\left( {1 + {S_{ij}}} \right)\log \frac{1}{{1 + {e^{ - \sigma \left( {{s_i} - {s_j}} \right)}}}} - \frac{1}{2}\left( {1 - {S_{ij}}} \right)\log \frac{{{e^{ - \sigma \left( {{s_i} - {s_j}} \right)}}}}{{1 + {e^{ - \sigma \left( {{s_i} - {s_j}} \right)}}}}\\ = - \frac{1}{2}\left( {1 + {S_{ij}}} \right)\log \frac{1}{{1 + {e^{ - \sigma \left( {{s_i} - {s_j}} \right)}}}} - \frac{1}{2}\left( {1 - {S_{ij}}} \right)\left[ { - \sigma \left( {{s_i} - {s_j}} \right) + \log \frac{1}{{1 + {e^{ - \sigma \left( {{s_i} - {s_j}} \right)}}}}} \right]\\ = \frac{1}{2}\left( {1 - {S_{ij}}} \right)\sigma \left( {{s_i} - {s_j}} \right) + \log \left( {1 + {e^{ - \sigma \left( {{s_i} - {s_j}} \right)}}} \right) \end{array} Cij=−21(1+Sij)log1+e−σ(si−sj)1−21(1−Sij)log1+e−σ(si−sj)e−σ(si−sj)=−21(1+Sij)log1+e−σ(si−sj)1−21(1−Sij)[−σ(si−sj)+log1+e−σ(si−sj)1]=21(1−Sij)σ(si−sj)+log(1+e−σ(si−sj))
所以:
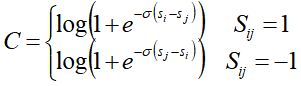
RankNet损失函数C具有对称性,即交换i和j的位置,损失函数的值不变
- 利用神经网络的反向传播对模型进行训练,使用损失函数对模型参数的求导,然后对模型参数进行迭代更新
- 通过调整参数的取值来逼近损失函数的最小值
- 采用SGD进行优化,对每一个pair对都会进行一次权重的更新
- 采用mini-batch learning的方式,是对同一个query下的所有doc进行一次权重的更新。时间消耗从O(n2)降到了O(n) => 加速RankNet的学习过程
- RankNet的训练数据为各查询下若干文档对,因此需针对文档对的输入去调整网络的权重
Ranklib
Ranklib:
- 开源工具,集成多种排序学习方法
- https://sourceforge.net/p/lemur/wiki/RankLib/
- MART(GBDT)
- RankNet
- RankBoost
- AdaRank
- Coordinate Ascent
- LambdaMART
- ListNet
- Random Forests
Ranklib使用: - java -jar RankLib.jar

例如用使用Ranklib进行排序学习:
训练数据:MQ2008/Fold1/train.txt
测试数据:MQ2008/Fold1/test.txt
验证数据:MQ2008/Fold1/vali.txt
排名算法:6,LambdaMART
评估指标:NDCG,取排名前 10 个数据进行计算
测试数据评估指标:NDCG,取排名前 8 个数据进行计算
保存模型:mymodel.txt
java -jar RankLib-patched.jar -train MQ2008/Fold1/train.txt -test MQ2008/Fold1/test.txt -validate MQ2008/Fold1/vali.txt -ranker 6 -metric2t NDCG@10 -metric2T NDCG@8 -save mymodel.txt