多目标优化算法包pymoo参考指南
多目标优化算法包pymoo参考指南
1 多目标函数定义
在不损失任何通用性的情况下,优化问题可以定义为:
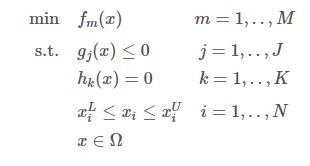
式中:
- x i x_i xi 为第 i i i 个待优化变量;
- x i L x^L_i xiL 和 x i U x^U_i xiU 为其下界和上界;
- f m f_m fm 为第 m m m 个目标函数;
- g j g_j gj 为第 j j j 个不等式约束;
- h k h_k hk 为第 k k k 个等式约束。
目标函数 f f f 应满足所有的等式和不等式约束。如果一个特定的目标函数是最大化( max f i \max f_i maxfi),可以重新定义问题以最小化其负值( min − f i \min - f_i min−fi)。
在优化问题上需要考虑以下几个方面:
1) 变量类型
变量涵盖了优化问题的搜索空间Ω。不同的变量类型,如连续、离散/整数、二进制或排列,定义了搜索空间的特征。在某些情况下,变量类型甚至可能是混合的,这进一步增加了复杂性。
2) 变量个数
不仅是类型,而且**变量的数量(N)**也是必不可少的。可以想象解决一个只有十个变量的问题和解决一个有几千个变量的问题是完全不同的。对于大规模优化问题,即使二阶导数的计算也非常昂贵,有效地处理内存起着更重要的作用。
3) 目标数量
有些优化问题有多个相互冲突的目标(M>1)待优化。
单目标优化只是M=1的特例。在多目标优化中,解支配着单目标优化中标量的比较。在目标空间中有多个维度,最优(大多数时候)由一组非支配解组成。因为要获得一组解,所以基于种群的算法主要用作求解器。
4) 约束
优化问题有两种约束:不等式(g)约束和等式(h)约束。
无论解决方案的目标有多好,如果它最终只违反了一个约束,就被认为是不可行的。
约束对问题的复杂性有很大的影响。例如,如果搜索空间中只有少数解可行,或者需要满足大量的约束(|J|+|K|)。对于遗传算法来说,满足等式约束是相当具有挑战性的。因此,需要以不同的方式解决这个问题,例如,通过将搜索空间映射到总是满足等式约束的实用空间,或者通过定制注入等式约束的知识。
5) 多模态
在多模态适应度场景下,由于存在少量甚至大量的局部最优,优化变得更加困难。对于所找到的解,必须总是问,该方法是否在搜索空间中探索了足够的区域,以最大化获得全局最优的概率。多模态搜索空间会迅速显示出局部搜索的局限性,容易陷入困境。
6) 可微性
一个可微的函数意味着可以计算一阶甚至二阶导数。可微函数允许使用基于梯度的优化方法,这比无梯度方法有很大的优势。大多数基于梯度的算法都是基于逐点的,对于单模态的适应度场景非常高效。然而,在实践中,函数通常是不可微的,或者更复杂的函数需要全局搜索而不是局部搜索。在不知道数学优化的情况下解决问题的研究领域也被称为黑盒优化。
7) 不确定性。
通常假设目标函数和约束函数是确定性的。然而,如果一个或多个目标函数是不确定的,这就会引入噪声或也称为不确定性。解决潜在随机性的一种技术是对不同的随机种子重复评估并平均结果值。此外,从多个评估中得到的标准偏差可以用来确定特定解决方案的性能和可靠性。一般来说,具有潜在不确定性的优化问题是由随机优化研究领域来研究的。
2 双目标优化问题
双目标优化问题:
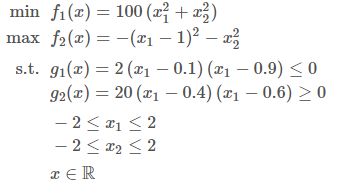
上述问题中:
- 存在两个目标函数( M = 2 M=2 M=2),其中最小化 f 1 ( x ) f_1(x) f1(x),最大化 f 2 ( x ) f_2(x) f2(x)。
- 优化目标存在两个不等式约束( J = 2 J=2 J=2),其中 g 1 ( x ) g_1(x) g1(x) 是小于等于, g 2 ( x ) g_2(x) g2(x) 是大于等于。
- 问题由两个变量定义( N = 2 N=2 N=2), x 1 x_1 x1 和 x 2 x_2 x2 ,两者的范围都在 [ − 2 , 2 ] [-2,2] [−2,2]。
- 该优化问题不包含等式约束( K = 0 K=0 K=0)。
首先分析 Pareto 最优解的位置。
f 1 ( x ) f_1(x) f1(x) 的最小值在 ( 0 , 0 ) (0,0) (0,0) 处, f 2 ( x ) f_2(x) f2(x) 的最大值在 ( 1 , 0 ) (1,0) (1,0) 处。由于这两个函数都是二次函数,因此最优解由两个最优解之间的一条直线给出。这意味着所有pareto最优解(暂时忽略约束条件)具有共同的 x 2 = 0 x_2=0 x2=0 和 x 1 ∈ ( 0 , 1 ) x1\in(0,1) x1∈(0,1)。
第一个约束仅依赖于 x 1 x_1 x1,且满足 x 1 ∈ ( 0.1 , 0.9 ) x_1\in(0.1,0.9) x1∈(0.1,0.9)。 x 1 ∈ ( 0.4 , 0.6 ) x_1 \in(0.4,0.6) x1∈(0.4,0.6) 满足第二个约束 g 2 g_2 g2。这意味着从解析的角度,帕累托最优集为:
P S = { ( x 1 , x 2 ) ∣ ( 0.1 ≤ x 1 ≤ 0.4 ) ∨ ( 0.6 ≤ x 1 ≤ 0.9 ) ∧ x 2 = 0 } PS=\left\{\left(x_{1}, x_{2}\right) \mid\left(0.1 \leq x_{1} \leq 0.4\right) \vee\left(0.6 \leq x_{1} \leq 0.9\right) \wedge x_{2}=0\right\} PS={(x1,x2)∣(0.1≤x1≤0.4)∨(0.6≤x1≤0.9)∧x2=0}
通过绘制函数来查看帕累托最优集(橙色):
import numpy as np
X1, X2 = np.meshgrid(np.linspace(-2, 2, 500), np.linspace(-2, 2, 500))
F1 = X1**2 + X2**2
F2 = (X1-1)**2 + X2**2
G = X1**2 - X1 + 3/16
G1 = 2 * (X1[0] - 0.1) * (X1[0] - 0.9)
G2 = 20 * (X1[0] - 0.4) * (X1[0] - 0.6)
import matplotlib.pyplot as plt
plt.rc('font', family='serif')
levels = [0.02, 0.1, 0.25, 0.5, 0.8]
plt.figure(figsize=(7, 5))
CS = plt.contour(X1, X2, F1, levels, colors='black', alpha=0.5)
CS.collections[0].set_label("$f_1(x)$")
CS = plt.contour(X1, X2, F2, levels, linestyles="dashed", colors='black', alpha=0.5)
CS.collections[0].set_label("$f_2(x)$")
plt.plot(X1[0], G1, linewidth=2.0, color="green", linestyle='dotted')
plt.plot(X1[0][G1<0], G1[G1<0], label="$g_1(x)$", linewidth=2.0, color="green")
plt.plot(X1[0], G2, linewidth=2.0, color="blue", linestyle='dotted')
plt.plot(X1[0][X1[0]>0.6], G2[X1[0]>0.6], label="$g_2(x)$",linewidth=2.0, color="blue")
plt.plot(X1[0][X1[0]<0.4], G2[X1[0]<0.4], linewidth=2.0, color="blue")
plt.plot(np.linspace(0.1,0.4,100), np.zeros(100),linewidth=3.0, color="orange")
plt.plot(np.linspace(0.6,0.9,100), np.zeros(100),linewidth=3.0, color="orange")
plt.xlim(-0.5, 1.5)
plt.ylim(-0.5, 1)
plt.xlabel("$x_1$")
plt.ylabel("$x_2$")
plt.legend(loc='upper center', bbox_to_anchor=(0.5, 1.12),
ncol=4, fancybox=True, shadow=False)
plt.tight_layout()
plt.show()
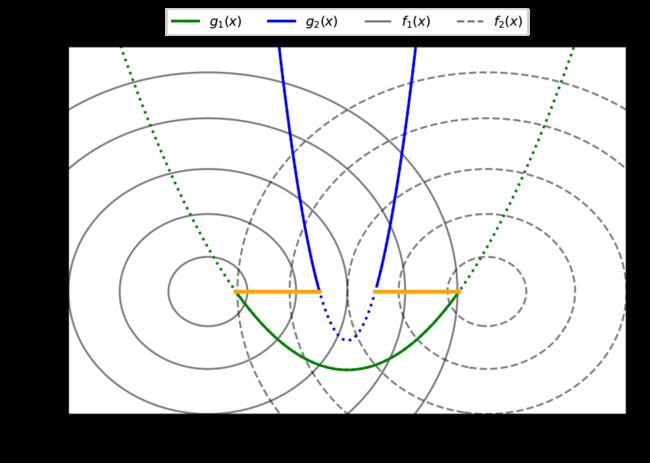
接下来,通过将pareto集映射到目标空间来导推导出Pareto-front。Pareto-front equation 基于 f 2 f_2 f2 并取决于 f 1 f_1 f1 的变量。
我们知道最优在 x 2 = 0 x_2=0 x2=0 这意味着可以将目标函数简化为 f 1 ( x ) = 100 x 1 2 , f 2 ( x ) = − ( x 1 − 1 ) 2 f_1(x)=100 x^2_1, f_2(x)= -(x_1-1)^2 f1(x)=100x12,f2(x)=−(x1−1)2。第一个目标 f 1 f_1 f1 可以转化为 x 1 = f 1 100 x_1=\sqrt{\frac{f_1}{100}} x1=100f1,然后放入第二个目标,结果为:
f 2 = − ( f 1 100 − 1 ) 2 f_{2}=-\left(\sqrt{\frac{f_{1}}{100}}-1\right)^{2} f2=−(100f1−1)2
方程定义了形状,接下来需要定义 f 1 f_1 f1 的所有可能值。如果将 x 1 x_1 x1 的值代入 f 1 f_1 f1,就得到感兴趣的点 [ 1 , 16 ] [1,16] [1,16] 和 [ 36 , 81 ] [36,81] [36,81]。因此,Pareto-front 为:
import numpy as np
import matplotlib.pyplot as plt
plt.figure(figsize=(7, 5))
f2 = lambda f1: - ((f1/100) ** 0.5 - 1)**2
F1_a, F1_b = np.linspace(1, 16, 300), np.linspace(36, 81, 300)
F2_a, F2_b = f2(F1_a), f2(F1_b)
plt.rc('font', family='serif')
plt.plot(F1_a,F2_a, linewidth=2.0, color="green", label="Pareto-front")
plt.plot(F1_b,F2_b, linewidth=2.0, color="green")
plt.xlabel("$f_1$")
plt.ylabel("$f_2$")
plt.legend(loc='upper center', bbox_to_anchor=(0.5, 1.10),
ncol=4, fancybox=True, shadow=False)
plt.tight_layout()
plt.show()
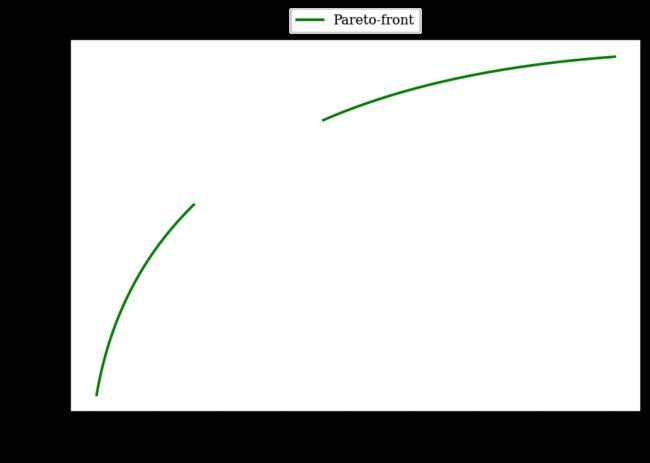
从图中可以看出这是一个非支配集。对于这个优化问题,第一个目标是最小化,第二个目标是最大化,更好的解决方案位于左上角。
3 使用pymoo优化目标
大多数优化框架致力于最小化或最大化所有目标,并且只有≤或≥约束。在pymoo中,每个目标函数都应该是最小的,每个约束都需要以≤0的形式提供。
因此,需要将一个应该被−1最大化的目标相乘,然后将其最小化。这导致最小化 − f 2 ( x ) −f_2(x) −f2(x),而不是最大化 f 2 ( x ) f_2(x) f2(x)。
此外,不等式约束需要表述为小于零(≤0)约束。因此,将 g 2 ( x ) g_2(x) g2(x) 乘以 −1,以翻转不等式关系。
此外,建议对约束进行规范化,使它们在相同的规模上运行,并给予它们同等的重要性。对于 g 1 ( x ) g_1(x) g1(x),系数为 2 ⋅ ( − 0.1 ) ⋅ ( − 0.9 ) = 0.18 2⋅(−0.1)⋅(−0.9)=0.18 2⋅(−0.1)⋅(−0.9)=0.18, g 2 ( x ) g_2(x) g2(x),系数为 20 ⋅ ( − 0.4 ) ⋅ ( − 0.6 ) = 4.8 20⋅(−0.4)⋅(−0.6)=4.8 20⋅(−0.4)⋅(−0.6)=4.8。
通过用 g 1 ( x ) g_1(x) g1(x) 和 g 2 ( x ) g_2(x) g2(x) 除以其相应的系数来实现约束的归一化。
最终目标函数为:
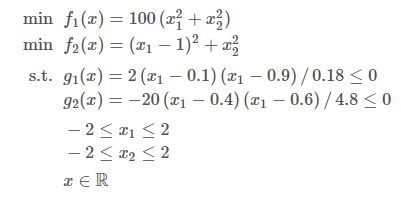
pymoo 安装:
pip install -U pymoo
1) 基于元素的问题定义
定义了一个继承自ElementwiseProblem的新的Python目标,并设置了正确的属性,比如目标的数量(n_obj)和约束的数量(n_constr)以及下限(xl)和上限(xu)。
负责评估的函数是_evaluate。函数的接口是参数 x x x 和 o u t out out。对于这个基于元素的实现, x x x 是一个长度为 n_var 的一维NumPy数组,表示要计算的单个解决方案。 o u t out out 是字典。
目标值应该以长度为 n_obj 的NumPy数组列表的形式写到 out["F"],约束写到长度为n_constr的out["G"]。
import numpy as np
from pymoo.core.problem import ElementwiseProblem
class MyProblem(ElementwiseProblem):
def __init__(self):
super().__init__(n_var=2,
n_obj=2,
n_constr=2,
xl=np.array([-2,-2]),
xu=np.array([2,2]))
def _evaluate(self, x, out, *args, **kwargs):
f1 = 100 * (x[0]**2 + x[1]**2)
f2 = (x[0]-1)**2 + x[1]**2
g1 = 2*(x[0]-0.1) * (x[0]-0.9) / 0.18
g2 = - 20*(x[0]-0.4) * (x[0]-0.6) / 4.8
out["F"] = [f1, f2]
out["G"] = [g1, g2]
problem = MyProblem()
一个问题可以用几种不同的方式定义。上面演示了一个基于元素的实现,这意味着每次为每个解决方案 x x x 调用_evaluate。
另一种方法是向量化的,其中 x x x 表示一组完整的解决方案或一种函数式的、可能更python化的方法,它以函数的形式提供每个目标和约束。
详见:
https://pymoo.org/problems/definition.html
2) 初始化算法
pymoo算法列表:
| 算法 |
|---|
| 1. 遗传算法 GA,单目标 |
| 2. 差分进化 DE,单目标 |
| 3. 偏置随机密钥遗传算法 BRKGA,单目标 |
| 4. 单纯形 NelderMead,单目标 |
| 5. 模式搜索 PatternSearch,单目标 |
| 6. CMAES,单目标 |
| 7. 进化策略 ES,单目标 |
| 8. 随机排序进化策略 SRES,单目标 |
| 9. 改进的随机排序进化策略 ISRES,单目标 |
| 10. NSGA-II,NSGA2,多目标 |
| 11. R-NSGA-II,RNSGA2,多目标 |
| 12. NSGA-III,NSGA3,多目标 |
| 13. U-NSGA-III,UNSGA3,单目标和多目标 |
| 14. R-NSGA-III,RNSGA3,单目标和多目标 |
| 15. 多目标分解 MOEAD,单目标和多目标 |
| 16. AGE-MOEA,单目标和多目标 |
| 17. C-TAEA,单目标和多目标 |
详见:
https://pymoo.org/algorithms/list.html#nb-algorithms-list
这里选择多目标算法NSGA-II 来进行说明。对于大多数算法,可以选择默认的超参数,或者通过修改它们创建自己的算法版本。
例如,对于这个相对简单的问题,选择群体大小为40 (pop_size=40),每代只有10个后代 (n_offsprings=10)。启用重复检查(eliminate_duplicate =True),确保交配产生的后代与它们自己和现有种群的设计空间值不同。
from pymoo.algorithms.moo.nsga2 import NSGA2
from pymoo.factory import get_sampling, get_crossover, get_mutation
algorithm = NSGA2(
pop_size=40,
n_offsprings=10,
sampling=get_sampling("real_random"),
crossover=get_crossover("real_sbx", prob=0.9, eta=15),
mutation=get_mutation("real_pm", eta=20),
eliminate_duplicates=True
)
3) 定义终止标准
此外,需要定义终止标准来启动优化过程。定义终止的最常见方法是限制函数计算的总次数或简单地限制算法的迭代次数。
此外,一些算法已经实现了它们自己的算法,例如当单纯形退化时使用Nelder-Mead,或者在使用供应商库时使用CMA-ES。由于这个问题的简单性,使用了一个相当小的40次迭代的算法
from pymoo.factory import get_termination
termination = get_termination("n_gen", 40)
终止标准的列表和解释详见:
https://pymoo.org/interface/termination.html
4) 优化
最后,用定义的算法和终止来解决这个问题。函数接口使用最小化方法。
默认情况下,最小化函数执行算法和终止对象的深度拷贝,以确保它们在函数调用期间不会被修改。这对于确保具有相同随机种子的重复函数调用最终得到相同的结果是很重要的。当算法终止时,最小化函数返回一个Result对象。
from pymoo.optimize import minimize
res = minimize(problem,
algorithm,
termination,
seed=1,
save_history=True,
verbose=True)
X = res.X
F = res.F

上图中每一行表示一次迭代。前两列是当前生成计数器和到目前为止的计算数。对于约束问题,第三第四列显示了当前总体中最小约束违例(cv (min))和平均约束违例(cv (avg))。接下来是非支配解的数量(n_nds)和代表目标空间移动的另外两个指标。
5) 可视化
import matplotlib.pyplot as plt
xl, xu = problem.bounds()
plt.figure(figsize=(7, 5))
plt.scatter(X[:, 0], X[:, 1], s=30, facecolors='none', edgecolors='r')
plt.xlim(xl[0], xu[0])
plt.ylim(xl[1], xu[1])
plt.title("Design Space")
plt.show()

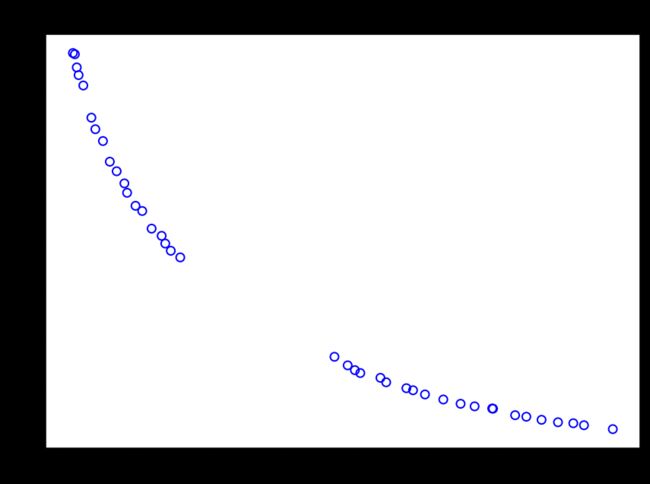
F = res.F
xl, xu = problem.bounds()
plt.figure(figsize=(7, 5))
plt.scatter(F[:, 0], F[:, 1], s=30, facecolors='none', edgecolors='blue')
plt.title("Objective Space")
plt.show()
4 多标准决策
得到一组非支配解后,决策者如何将这组解确定为少数甚至单个解。这种多目标问题的决策过程也被称为多准则决策(MCDM)。
1) 目标函数值归一化
在多目标优化中,需要考虑目标函数的尺度:
fl = F.min(axis=0)
fu = F.max(axis=0)
print(f"Scale f1: [{fl[0]}, {fu[0]}]")
print(f"Scale f2: [{fl[1]}, {fu[1]}]")
# Scale f1: [1.3377795039158837, 74.97223429467643]
# Scale f2: [0.01809179532919018, 0.7831767823138299]
可以看到,目标 f 1 f_1 f1 和 f 2 f_2 f2 的上界和下界有很大的不同,需要归一化。
在没有标准化的情况下,我们是在比较橙子和苹果。第一个目标由于其规模较大,将主导目标空间中的任何距离计算。处理不同规模的目标是任何多目标算法的固有部分,因此,需要对后处理做同样的事情。
一种常见的方法是使用所谓的理想点和最低点(ideal and nadir point)来规范。这里假设理想点和最低点(也称为边界点)和帕累托前沿(Pareto-front)是未知的。因此这些点可以近似值为:
approx_ideal = F.min(axis=0)
approx_nadir = F.max(axis=0)
plt.figure(figsize=(7, 5))
plt.scatter(F[:, 0], F[:, 1], s=30, facecolors='none', edgecolors='blue')
plt.scatter(approx_ideal[0], approx_ideal[1], facecolors='none', edgecolors='red', marker="*", s=100, label="Ideal Point (Approx)")
plt.scatter(approx_nadir[0], approx_nadir[1], facecolors='none', edgecolors='black', marker="p", s=100, label="Nadir Point (Approx)")
plt.title("Objective Space")
plt.legend()
plt.show()

通过以下方式对目标值进行归一化:
nF = (F - approx_ideal) / (approx_nadir - approx_ideal)
fl = nF.min(axis=0)
fu = nF.max(axis=0)
print(f"Scale f1: [{fl[0]}, {fu[0]}]")
print(f"Scale f2: [{fl[1]}, {fu[1]}]")
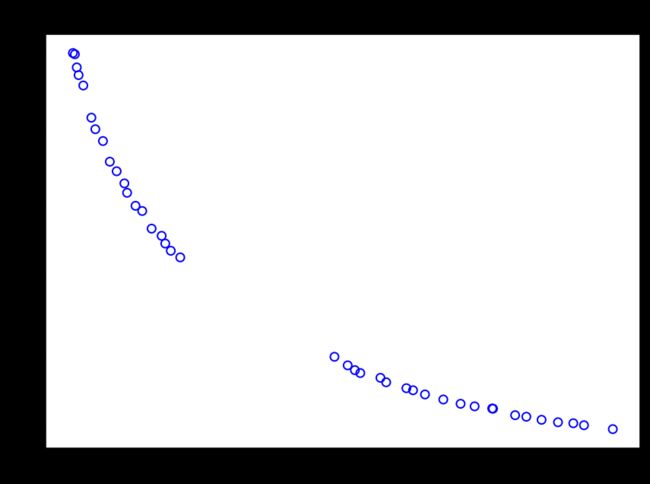
plt.figure(figsize=(7, 5))
plt.scatter(nF[:, 0], nF[:, 1], s=30, facecolors='none', edgecolors='blue')
plt.title("Objective Space")
plt.show()
# Scale f1: [0.0, 1.0]
# Scale f2: [0.0, 1.0]
2) 均衡规划(Compromise Programming)
其中一种做决策的方法是使用分解函数。需要定义反映使用者意愿的权重。矢量给出的权重仅为和为1的正浮点数,长度等于目标数。对于双目标问题,假设第一个目标没有第二个目标那么重要,则设置权重:
weights = np.array([0.2, 0.8])
接下来,选择增广尺度函数(Augmented Scalarization Function, ASF)分解方法。
from pymoo.decomposition.asf import ASF
decomp = ASF()
由于ASF应该是被最小化的,所以从所有的解中选择 最小的 ASF值。
为什么权重不是直接传递,而是1/weights?对于ASF,存在不同的公式,一个是值被除,另一个是值被乘。在“pymoo”中,“divide”并没有反映使用者的标准。因此,需要应用逆函数。
i = decomp.do(nF, 1/weights).argmin()
在找到解( i i i)后,可以按原来的比例来表示结果:
print("Best regarding ASF: Point \ni = %s\nF = %s" % (i, F[i]))
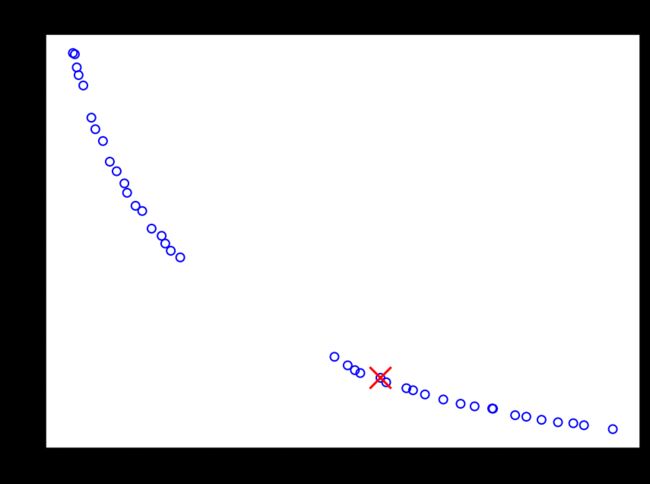
plt.figure(figsize=(7, 5))
plt.scatter(F[:, 0], F[:, 1], s=30, facecolors='none', edgecolors='blue')
plt.scatter(F[i, 0], F[i, 1], marker="x", color="red", s=200)
plt.title("Objective Space")
plt.show()
# Best regarding ASF: Point
# i = 21
# F = [43.28059434 0.12244878]
这种方法的一个好处是可以使用任何类型的分解函数。
3) 伪权重(Pseudo-Weights)
在多目标优化环境中,从解集中选择解的一种简单方法是伪权向量方法。分别计算第 i i i 个目标函数的伪权重 w i w_i wi:
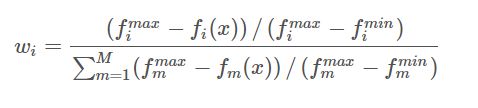
这个方程计算每个目标 i i i 到最差解的归一化距离。请注意,对于非凸帕累托合集,伪权重不对应于使用加权和的优化结果。然而,对于凸帕累托合集,伪权值表示目标空间中的位置。
from pymoo.mcdm.pseudo_weights import PseudoWeights
i = PseudoWeights(weights).do(nF)
print("Best regarding Pseudo Weights: Point \ni = %s\nF = %s" % (i, F[i]))
plt.figure(figsize=(7, 5))
plt.scatter(F[:, 0], F[:, 1], s=30, facecolors='none', edgecolors='blue')
plt.scatter(F[i, 0], F[i, 1], marker="x", color="red", s=200)
plt.title("Objective Space")
plt.show()
# Best regarding Pseudo Weights: Point
# i = 39
# F = [58.52211061 0.06005482]

5 收敛性分析
收敛分析应考虑两种情况,i) 帕累托合集是未知的,或 ii) 帕累托合集已被解析导出,或一个合理的近似存在。
1) 收敛性可视化
为了进一步检查结果与解析导出的最优匹配程度,必须将目标空间值转换为第二个目标 f 2 f_2 f2 最大化的原始定义。然后绘制Pareto-front图显示算法能够收敛的程度。
from pymoo.util.misc import stack
class MyTestProblem(MyProblem):
def _calc_pareto_front(self, flatten=True, *args, **kwargs):
f2 = lambda f1: ((f1/100) ** 0.5 - 1)**2
F1_a, F1_b = np.linspace(1, 16, 300), np.linspace(36, 81, 300)
F2_a, F2_b = f2(F1_a), f2(F1_b)
pf_a = np.column_stack([F1_a, F2_a])
pf_b = np.column_stack([F1_b, F2_b])
return stack(pf_a, pf_b, flatten=flatten)
def _calc_pareto_set(self, *args, **kwargs):
x1_a = np.linspace(0.1, 0.4, 50)
x1_b = np.linspace(0.6, 0.9, 50)
x2 = np.zeros(50)
a, b = np.column_stack([x1_a, x2]), np.column_stack([x1_b, x2])
return stack(a,b, flatten=flatten)
problem = MyTestProblem()
检验问题(test problems)的Pareto front可以通过以下方式实现:
pf_a, pf_b = problem.pareto_front(use_cache=False, flatten=False)
pf = problem.pareto_front(use_cache=False, flatten=True)
plt.figure(figsize=(7, 5))
plt.scatter(F[:, 0], F[:, 1], s=30, facecolors='none', edgecolors='b', label="Solutions")
plt.plot(pf_a[:, 0], pf_a[:, 1], alpha=0.5, linewidth=2.0, color="red", label="Pareto-front")
plt.plot(pf_b[:, 0], pf_b[:, 1], alpha=0.5, linewidth=2.0, color="red")
plt.title("Objective Space")
plt.legend()
plt.show()
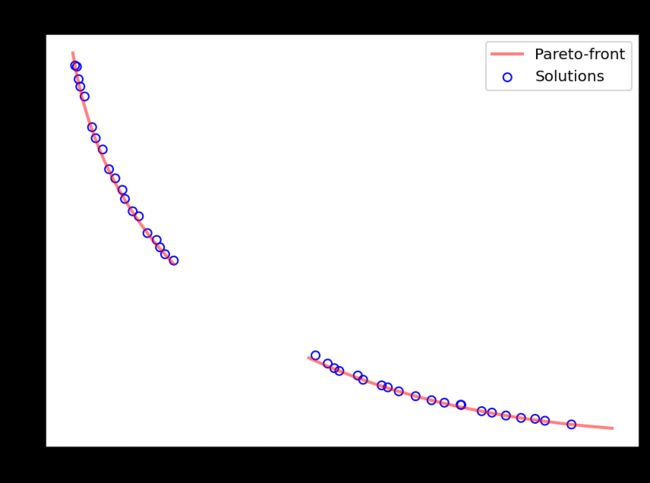
高维空间的绘制可参考:
https://pymoo.org/visualization/index.html
此外也可以使用 save_history=True 来查看收敛性:
from pymoo.optimize import minimize
res = minimize(problem,
algorithm,
("n_gen", 40),
seed=1,
save_history=True,
verbose=False)
X, F = res.opt.get("X", "F")
hist = res.history
print(len(hist)) # 40
n_evals = [] # corresponding number of function evaluations\
hist_F = [] # the objective space values in each generation
hist_cv = [] # constraint violation in each generation
hist_cv_avg = [] # average constraint violation in the whole population
for algo in hist:
# store the number of function evaluations
n_evals.append(algo.evaluator.n_eval)
# retrieve the optimum from the algorithm
opt = algo.opt
# store the least contraint violation and the average in each population
hist_cv.append(opt.get("CV").min())
hist_cv_avg.append(algo.pop.get("CV").mean())
# filter out only the feasible and append and objective space values
feas = np.where(opt.get("feasible"))[0]
hist_F.append(opt.get("F")[feas])
2) 约束满足
首先,查看什么时候找到了第一个可行的解决方案:
k = np.where(np.array(hist_cv) <= 0.0)[0].min()
print(f"At least one feasible solution in Generation {k} after {n_evals[k]} evaluations.")
# At least one feasible solution in Generation 0 after 40 evaluations.
# replace this line by `hist_cv` if you like to analyze the least feasible optimal solution and not the population
vals = hist_cv_avg
k = np.where(np.array(vals) <= 0.0)[0].min()
print(f"Whole population feasible in Generation {k} after {n_evals[k]} evaluations.")
plt.figure(figsize=(7, 5))
plt.plot(n_evals, vals, color='black', lw=0.7, label="Avg. CV of Pop")
plt.scatter(n_evals, vals, facecolor="none", edgecolor='black', marker="p")
plt.axvline(n_evals[k], color="red", label="All Feasible", linestyle="--")
plt.title("Convergence")
plt.xlabel("Function Evaluations")
plt.ylabel("Constraint Violation")
plt.legend()
plt.show()
# Whole population feasible in Generation 8 after 120 evaluations.
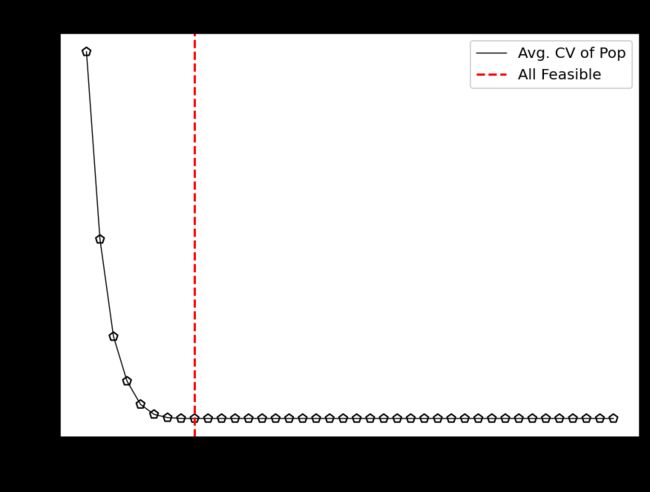
3) Pareto合集未知
在Pareto-front未知的情况下,无法知道算法是否收敛到真正最优。至少没有进一步的信息。但是,可以看到算法在优化过程中什么时候取得了大部分的进展,以及迭代次数应该是少还是多。Hypervolume可用于比较两种算法。
Hypervolume是基于边界标准化的集(概念),用于多目标问题的性能指标。它符合帕累托标准,并基于预定义的参考点和提供的解决方案之间的容量。因此,hypervolume需要定义一个参考点ref_point,该参考点必须大于Pareto front的最大值。
# 在多目标优化中,归一化是非常重要的
approx_ideal = F.min(axis=0)
approx_nadir = F.max(axis=0)
from pymoo.indicators.hv import Hypervolume
metric = Hypervolume(ref_point= np.array([1.1, 1.1]),
norm_ref_point=False,
zero_to_one=True,
ideal=approx_ideal,
nadir=approx_nadir)
hv = [metric.do(_F) for _F in hist_F]
plt.figure(figsize=(7, 5))
plt.plot(n_evals, hv, color='black', lw=0.7, label="Avg. CV of Pop")
plt.scatter(n_evals, hv, facecolor="none", edgecolor='black', marker="p")
plt.title("Convergence")
plt.xlabel("Function Evaluations")
plt.ylabel("Hypervolume")
plt.show()
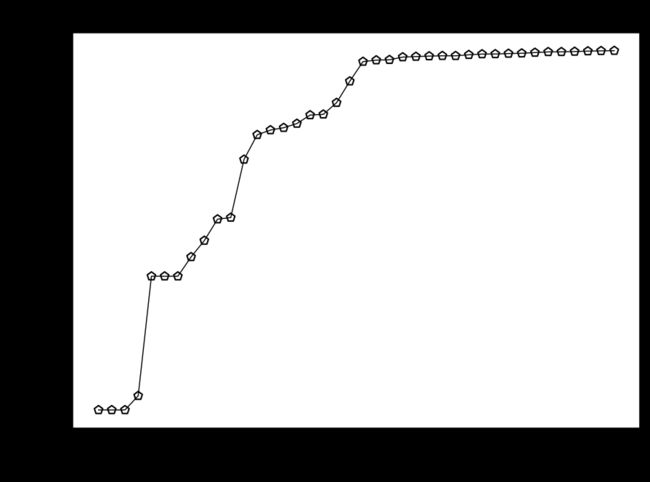
随着维数的增加,Hypervolume的计算成本会增加。其可以有效地计算出2个和3个目标的精确Hypervolume。对于更高的维度,一些研究人员使用hypervolume approximation,这在pymoo中还不可用。
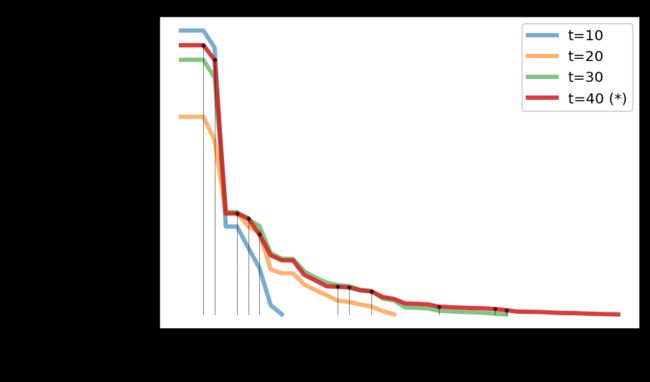
当真正的帕累托前沿未知时,另一种分析运行的方法是最近提出的running metric。运行度量显示了不同代之间目标空间的差异,并利用算法的生存能力将改进可视化。在pymoo中,如果没有定义默认终止标准,则使用此度量来确定多目标优化算法的终止。
例如,通过分析可以发现,从第4代到第5代,算法有了显著的改进。
from pymoo.util.running_metric import RunningMetric
running = RunningMetric(delta_gen=5,
n_plots=3,
only_if_n_plots=True,
key_press=False,
do_show=True)
for algorithm in res.history[:15]:
running.notify(algorithm)

绘制直到种群显示收敛,这里只做了轻微的改进:
from pymoo.util.running_metric import RunningMetric
running = RunningMetric(delta_gen=10,
n_plots=4,
only_if_n_plots=True,
key_press=False,
do_show=True)
for algorithm in res.history:
running.notify(algorithm)
4) 帕累托合集是已知的或近似的
对于实际问题,必须使用近似。通过多次运行算法,从所有解集中提取非支配解,就可以得到近似解。如果只有一次运行,另一种选择是使用得到的非支配解集作为近似。但是,结果仅反映了算法收敛到最终集合的进度。
from pymoo.indicators.igd import IGD
metric = IGD(pf, zero_to_one=True)
igd = [metric.do(_F) for _F in hist_F]
plt.plot(n_evals, igd, color='black', lw=0.7, label="Avg. CV of Pop")
plt.scatter(n_evals, igd, facecolor="none", edgecolor='black', marker="p")
plt.axhline(10**-2, color="red", label="10^-2", linestyle="--")
plt.title("Convergence")
plt.xlabel("Function Evaluations")
plt.ylabel("IGD")
plt.yscale("log")
plt.legend()
plt.show()
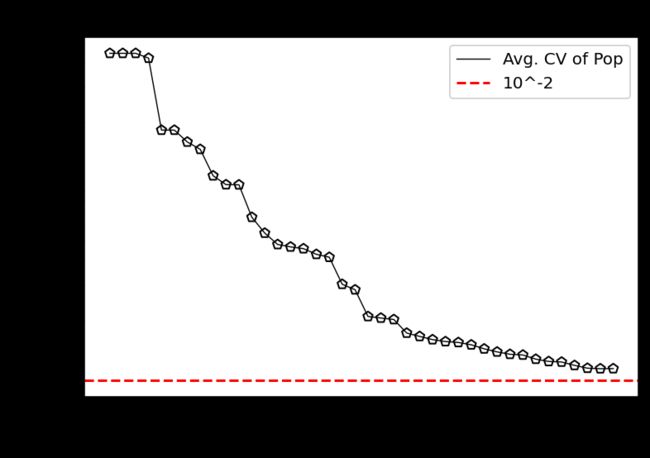
from pymoo.indicators.igd_plus import IGDPlus
metric = IGDPlus(pf, zero_to_one=True)
igd = [metric.do(_F) for _F in hist_F]
plt.plot(n_evals, igd, color='black', lw=0.7, label="Avg. CV of Pop")
plt.scatter(n_evals, igd, facecolor="none", edgecolor='black', marker="p")
plt.axhline(10**-2, color="red", label="10^-2", linestyle="--")
plt.title("Convergence")
plt.xlabel("Function Evaluations")
plt.ylabel("IGD+")
plt.yscale("log")
plt.legend()
plt.show()

指标详见:
https://pymoo.org/misc/indicators.html
参考:
https://pymoo.org/index.html