李宏毅机器学习笔记——神经网络设计的技巧

极小值与鞍点

优化失败的原因可能是：

1. 陷入局部最优（极小值）
2. 当前为鞍点（不是局部最优，但梯度为零）
   以上统称为 critical point。

数学工具

想知道当前Loss Function是哪种情况，最好的办法就是把函数图像描绘出来。但描绘整个函数形状通常是比较难的一件事情，我们退而求其次，描绘当前点的局部函数图像。这里我们用到泰勒展开公式。

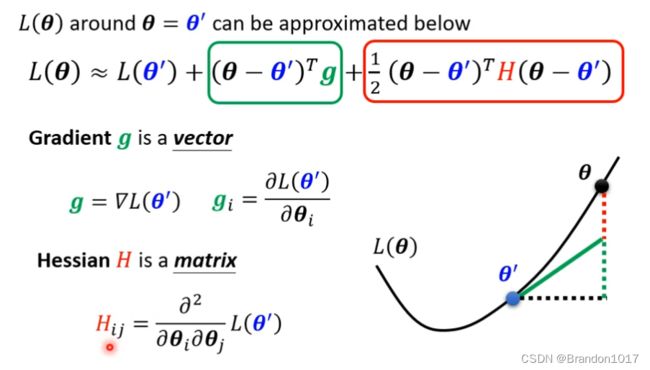
若当前梯度为零 ，则绿色框框内的值为零，所以我们主要看红色框框内的式子：


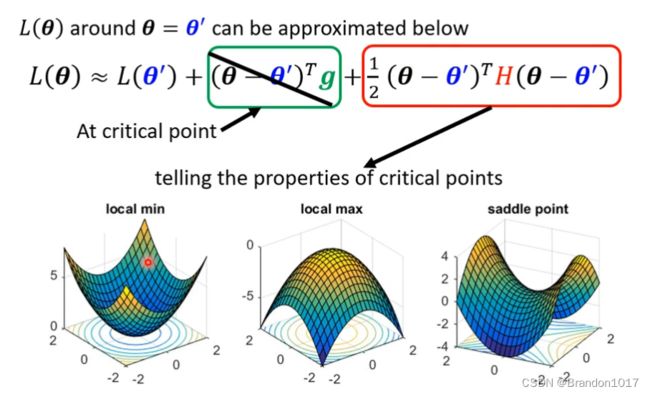
如图所示，我们只用计算黑塞矩阵 $H$ 的特征值，来判断它是正定or负定or其它。

如果是鞍点（Sadlle point）的话，我们取为负值的特征值 $\lambda$，对应的特征向量为 $\mathbf{u}$，则有 ${\mathbf{u}}^{T}H\mathbf{u}={\mathbf{u}}^T(\lambda \mathbf{u})=\lambda ||\mathbf{u}|{|}^2<0$.
于是我们可以令 $\theta -{\theta }^{\prime }=\mathbf{u}$, 将其带入 $L(\theta )\approx L({\theta }^{\prime })+\frac{1}{2}(\theta -{\theta }^{\prime }{)}^{T}H(\theta -{\theta }^{\prime })$，推出 $L(\theta )<L({\theta }^{\prime })$。那么我们只需将参数往方向$\mathbf{u}$更新即可。

鞍点与局部最小值

一般来说，我们的模型特征数很多，几十几百甚至上万，所以Loss Function中的黑塞矩阵是正定的几率十分小，于是鞍点是我们实际中遇到情况最多的。

批次（Batch）与动量（Momentum）

Batch

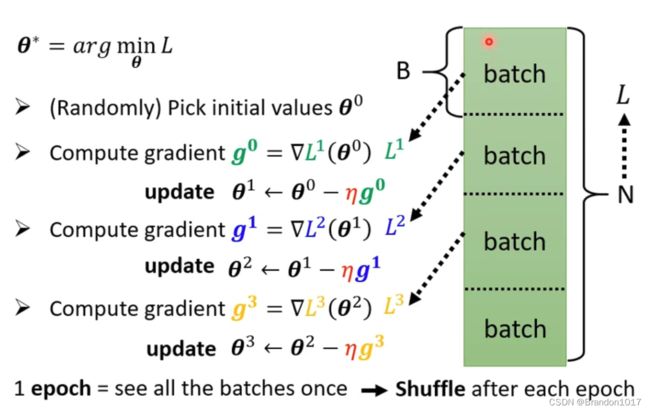
我们在训练的时候，会将训练集分成多个batch，每个batch里面的data数量都是相当的。当我们做梯度下降参数更新时，都是拿一个batch进行计算更新，待所有batch都轮流计算过后，再重新将batch顺序打乱（Shuffle），进行下一轮的参数更新。

为什么要用batch

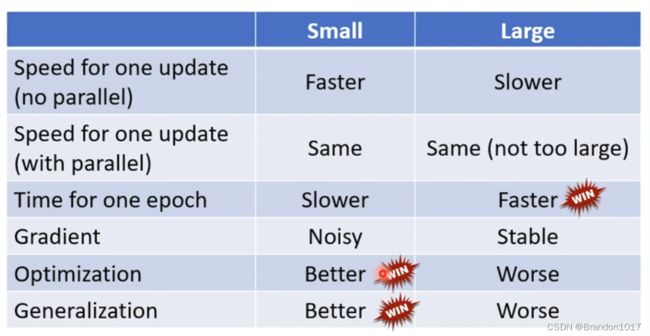
如果不用batch的方式，而是用传统的（或者说Batch size等于N）将所有训练集样本计算出Loss Function进行更新，缺点是参数更新速度会比较慢，优点是参数更新的方向比较准确。

如果采用batch的方式（Batch size小于N），优点是更新速度快，所有训练集样本计算完后参数更新了Batch的组数次，缺点是参数更新的方向不是很准确，有噪音。

以上结论不考虑采用GPU运算（平行运算）。

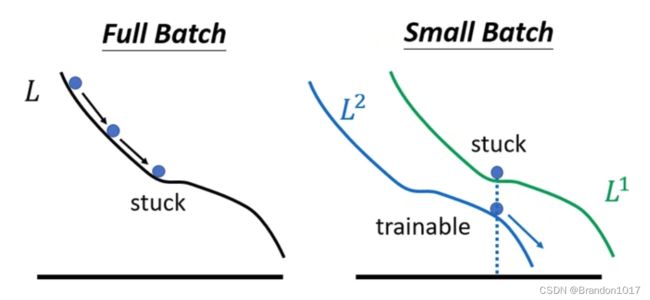
另外，如果用Full Batch（Batch size等于N）计算模型的参数，最终模型得到准确率反而没有Small Batch算出来的模型要好，原因是因为用Full Batch算的Loss Function永远是一样的，会陷入局部最优解或者是鞍点；而用Small Batch算的Loss Function，每个Batch对应的函数略有不同，可能在一个Batch上的函数陷入局部最优解了，在另一个Batch上的函数反而可以继续更新，从而使得整体模型的参数也可以不断更新。

Momentum

参考了物理中动量的含义。在进行梯度下降更新时，我们希望到达Loss Function的一个梯度为0的地方时（极小值或鞍点），还可以有能力继续往更新的方向前进，使得可以脱离局部最小值。

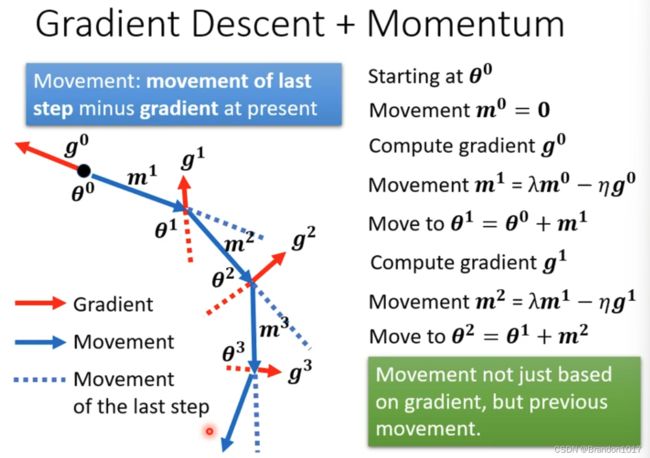
在更新参数时，我们计算梯度会加上上一次计算出来的梯度进行更新。

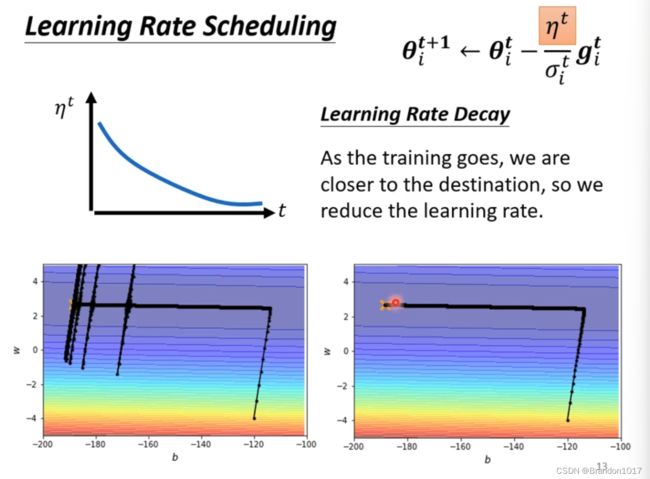
自适应学习率 Adaptive Learning Rate

通常情况下Critical point可能不是我们训练中最主要的问题。有时候我们发现loss已经很小了，不再下降，然而梯度并没有等于零，而且还在不断震荡。

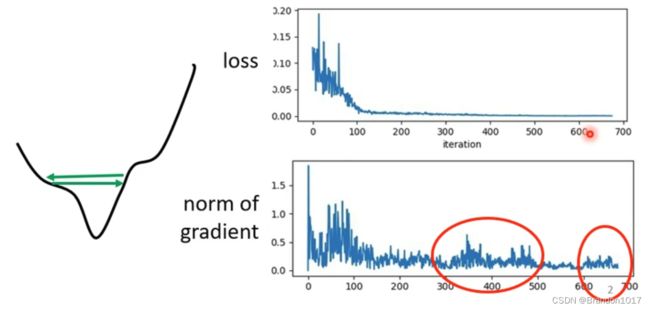
我们需要修正学习率，让它能够根据当前的梯度特征来调节大小。
因此我们修改梯度更新参数的式子：KaTeX parse error: Undefined control sequence: \etag at position 27: …}_i=\theta^t_i-\̲e̲t̲a̲g̲^t_i ⇒ ${\theta }_i^{t+1}={\theta }_i^t-\frac{\eta }{{\sigma }_i^t}{g}_i^t$. 我们下面要寻找合适的 ${\sigma }_i^t$。

根号平方根 Root Mean Square

参考之前误差与平均的笔记中 Adagrad 方法。它是模拟Loss Function的二次导函数的大小，来调节学习率。

但这种方法学习率不能在一个维度方向上动态地调整，所以还有待改进。

RMSProp

其中 $\alpha$ 确定权重。

Adam

分类 Classification

One-hot 编码

可以避免类与类之间的差异存在大小。

最后将 $\mathbf{y}$进行softmax操作： $y_i^{\prime }=\frac{exp(y_i)}{{\Sigma }_{j}exp(y_i)}$。
softmax将 $\mathbf{y}$ 的值符合概率分布。

Loss Function

在分类任务中，常见的Loss Function是交叉熵（Cross-entropy）：$e=-{\Sigma }_i{\hat{y}}_{i}ln{y}_i^{\prime }$.
交叉熵与Softmax常常一起出现。

Batch Normalization

我们想简化Loss Function，使得训练更加容易 ⇒ 考虑是什么影响了Loss Function的形状 ⇒ data特征的量纲对Loss Function会有影响。于是我们就有了特征标准化。

Feature Normalization

将特征统一进行标准化：$x_i^r=\frac{x_i^r-{\mu }_i}{{\sigma }_i}$

对于神经网络，每一层得到的中间值也需要继续标准化，再进入下一层。（可以在Sigmoid函数之前做标准化）

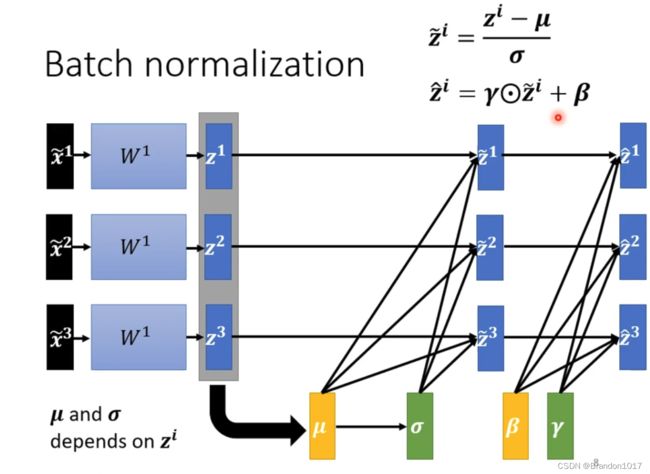
Batch Normalization

每一层继续标准化相当于加入了新的参数：$\mu$和$\sigma$。

Testing

在testing阶段，我们可能没有足够的数据来组成一个batch，但我们又需要及时进行计算，那我们就需要考虑Batches间$\mu$和$\sigma$的移动平均值。