机器学习第三章之线性回归模型

这一章主要介绍机器学习中非常基础且经典的线性回归模型，包括一元线性回归模型、线性回归模型的评估方法、多元线性回归模型等多方面内容，同时将介绍两个经典案例：不同行业的收入预测模型及客户价值预测模型来巩固所学知识点。

点击下载。

3.1 一元线性回归

线性回归模型是利用线性拟合的方式来探寻数据背后的规律，如下图所示，就是通过搭建线性回归模型来寻找这些散点（也称样本点）背后的趋势线（也称回归曲线），而通过这个回归曲线我们就能进行一些简单的预测分析或因果关系分析。

线性回归中，我们根据特征变量（也称自变量）来对反应变量（也称因变量）进行预测，根据特征变量的个数可将线性回归模型分为一元线性回归和多元线性回归，比如通过一个特征变量：工作年限对收入进行预测，就属于一元线性回归，而通过多个特征变量：工作年限、行业、所在城市等对收入进行预测，就属于多元线性回归。这一小节主要先讲解下一元线性回归模型。

3.1.1 一元线性回归的数学原理

一元线性回归模型也称为简单线性回归模型，其形式可以通过如下公式表达：

y = a*x + b

其中y为因变量，x为自变量，a表示回归系数，b表示截距。如下图所示，其中为实际值，为预测值，一元线性回归的目的就是拟合出一条线来使得预测值和实际值尽可能的接近，如果大部分点都落在拟合出来的线上，那么该线性回归模型则拟合较好。

那么该如何来衡量实际值与预测值接近的程度呢，数学上我们通过两者差值的平方和（该和也称为残差平方和）来进行衡量，公式如下，其中为求和符号。此外，补充说明一句，在机器学习领域，该残差平方和也被称之为回归模型的损失函数（更多损失函数的相关知识点可以参考本书第9章的补充知识点）。

显然我们希望这个和越小越好，这样实际值和预测值就更加接近，而数学上求最小值的方法为求导数，当导数为0时，该残差平方和最小。我们将残差平方和换一个表达形式，公式如下：

那么通过对残差平方和进行求导，然后令其导数为0便可以求得一元线性回归模型的系数a和截距b，这个便是一元线性回归的数学原理，学术上称其为最小二乘法，具体的求导的公式这里可以参考本节的补充知识点。而在Python中就有专门的库来求解这里的系数a和截距b，而不需要我们去计算复杂的数学公式，这个我们将在下一节进行讲解。

补充知识点：最小二乘法演示
我们以如下数据为例，来演示最小二乘法供感兴趣的读者参考：

假设线性回归模型的的拟合方程为y = ax + b，那么残差平方和或者说损失函数定义为：

拟合的目的便是使得残差平方和尽可能的小，也即真实值和预测值尽可能的接近。根据高等数学求极值的相关知识点，通过对残差平方和进行求导（对a和b进行求导），导数为0时，该残差平方和取极值，此时便能获得拟合所需要的系数a和截距b了。

y = x^2
y’ = 2x
y’ = 0 -> x = 0

根据高等数学复合求导的相关知识：又因为的导数为2x，所以的导数为分别对a和b求导，得到以下公式：
f = (2x+1)^2
f = 2(2x+1)*2

将x,y的值代入且等号两边同除以2，得到：

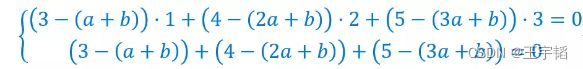
继续简化，得：

容易解得

也就是说拟合曲线为y=x+2，可以发现完美拟合了三个点，感兴趣的读者可以验证下，此时的残差平方和的确取最小值，且为0。此外，对于多元线性回归，其各个系数和截距的推导方法和上面的过程也是一致的，只不过变成了多元方程组而已。

3.1.2 一元线性回归的代码实现

通过Python的Scikit-learn库我们便可以轻松的搭建一元线性回归模型。如果是通过之前讲过的Anaconda安装的Python的话，那么Scikit-learn库已经默认被安装好了。这里我们以一个简单的例子来了解下如何在Python中搭建一元线性回归模型。
1.绘制散点图
首先通过之前学过的Matplotlib库先绘制几个散点，代码如下：

import matplotlib.pyplot as plt
X = [[1], [2], [4], [5]]
Y = [2, 4, 6, 8]
plt.scatter(X, Y)
plt.show()

这里有个小的注意点，其中自变量集合X需要写成二维结构形式，也即大列表里包含着小列表，这个其实是符合之后多元回归的逻辑，因为多元回归，一个因变量y可能对应着多个自变量x，比如对于三元线性回归(即有三个特征变量)，此时的自变量集合X就需要写成类似如下形式：

X = [[1, 2, 3], [2, 4, 5], [4, 6, 8], [5, 7, 9]]

至于因变量集合Y则写成一维的结构即可，此时的散点如下图所示：

2.引入Scikit-learn库搭建模型
有了原始数据后，我们引入Scikit-learn库便可快速搭建线性回归模型，代码如下：

from sklearn.linear_model import LinearRegression
regr = LinearRegression()
regr.fit(X,Y)

其中第1行代码为从Scikit-learn库引入线性回归的LinearRegression模块，第2行代码则是构造一个初始的线性回归模型并命名为regr，第3行代码通过fit()函数来完成模型搭建，此时的regr就已经是一个搭建好的线性回归模型了。

3.模型预测
regr已经是搭建好的模型了，此时就可以通过该模型来预测数据了，比如自变量是数字1.5，那么通过predict()函数就能预测当自变量x=1.5时对应的因变量y了，代码如下：

y = regr.predict([[1.5]])

意这里的自变量还是得写成二维结构的形式，原理和之前绘制散点图时写成二维结构数据类似，此时获得的预测结果y如下所示，此时获得y为一个一维数组。

[2.9]

此外，如果想同时预测多个自变量，则可以使用如下代码：

y = regr.predict([[1.5], [2.5], [4.5]])

此时的预测结果如下：

[2.9 4.3 7.1]

4.模型可视化
我们还可以将搭建好的模型可视化展示出来，代码如下：

plt.scatter(X, Y)
plt.plot(X, regr.predict(X))
plt.show()

此时的效果如下图所示，可以看到此时的一元线性回归模型就是中间形成的这条直线，其背后的原理就是3.1.1小节提到的最小二乘法 。

5.线性回归方程构造
可以通过coef_和intercept_得到此时直线的系数及截距，代码如下：

print('系数a为:' + str(regr.coef_[0]))
print('截距b为:' + str(regr.intercept_))

这里通过regr.coef_获得是一个列表，所以得通过regr.coef_[0]选取其中的元素，又因为该元素为数字，所以字符串拼接的时候需要利用str()函数转换成字符串，运行结果如下：

系数a为:1.4000000000000004
截距b为:0.7999999999999989

那么此时的一元线性回归得到的线性回归方程就可以表示为如下形式：

y = 1.4*x + 0.8

3.1.3 案例实战 ：不同行业工作年限与收入的线性回归模型

了解完一元线性回归模型的基本数学原理和常规代码实现后，我们来看一个具体的实战案例：通过一元线性回归模型搭建收入预测模型。
1.案例背景
通常来说，收入都会随着工作年限的增长而增长，而在不同的行业中收入的增长速度都会有所不同，本小节就是来通过一元线性回归模型来探寻工作年限对收入的影响，也即搭建收入预测模型，同时比较多个行业的收入预测模型来分析各个行业的特点。

2.读取数据
这里我们首先以目前比较火的IT行业为例，这里选取的是北京地区的IT行业工龄分布于0-8年的100个IT工程师月工资情况，通过如下代码读取数据，其中df.head()用来展示前5行数据。

import pandas
df = pandas.read_excel('IT行业收入表.xlsx')
df.head()  # 非Jupyter Notebook编辑器需要通过print()函数打印

此时数据如下：

此时的工龄为自变量，薪水为因变量，通过如下代码进行自变量、因变量选取：

X = df[['工龄']]
Y = df['薪水']

这里的自变量X必须写成二维数据结构，原因之前提过；而因变量Y写成一维的数据结构即可，不过其实写成二维的数组结构df[[‘薪水’]]，之后的模型也能运行。
通过如下代码可以将此时的散点图绘制出来：

import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.scatter(X,Y)
plt.xlabel('工龄')
plt.ylabel('薪水')
plt.show()

其中第2行代码用来显示中文，SimHei表示黑体字体。然后通过plt.xlabel()和plt.ylable()添加坐标轴标签，最后运行效果如下图所示：

3.模型搭建
根据3.1.2小节中的知识点，通过如下代码即可搭建线性回归模型：

from sklearn.linear_model import LinearRegression
regr = LinearRegression()
regr.fit(X,Y)

4.模型可视化
根据3.1.2小节中的知识点，通过如下代码即可将线性回归模型可视化呈现：

plt.scatter(X,Y)
plt.plot(X, regr.predict(X), color='red')  # color='red'设置为红色
plt.xlabel('工龄')
plt.ylabel('薪水')
plt.show()

此时运行效果如下图所示：

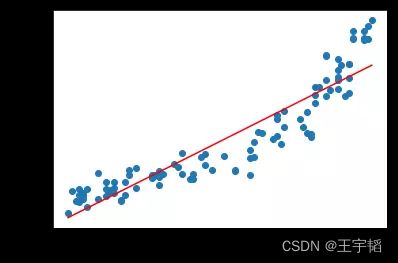
5.线性回归方程构造
我们还可以通过上一小节的知识点查看该直线的斜率系数a和截距b，代码如下：

print('系数a为:' + str(regr.coef_[0]))
print('截距b为:' + str(regr.intercept_))

运行结果如下：

系数a为:2497.1513476046866
截距b为:10143.131966873787

所以此时的一元线性回归曲线方程为：

y = 2497*x + 10143

完整代码如下所示：

# 1.读取数据
import pandas
df = pandas.read_excel('IT行业收入表.xlsx')
print(df.head())
X = df[['工龄']]
Y = df['薪水']

# 2.模型训练
from sklearn.linear_model import LinearRegression
regr = LinearRegression()
regr.fit(X,Y)

# 3.模型可视化
from matplotlib import pyplot as plt
plt.scatter(X,Y)
plt.plot(X, regr.predict(X), color='red')  # color='red'设置为红色
plt.xlabel('工龄')
plt.ylabel('薪水')
plt.show()

# 4.线性回归方程构造
print('系数a为:' + str(regr.coef_[0]))
print('截距b为:' + str(regr.intercept_))

补充知识点：模型优化 - 一元多次线性回归模型
对于一元线性回归模型而言，其实它还有一个进阶版本，叫作一元多次线性回归模型，比较常见的有一元二次线性回归模型，其格式如下：

y = a*x^2 + b*x + c

我们之所以还会研究一元多次线性回归模型，是因为有时真正契合的趋势线可能不是一条直线，而是一条曲线，比如下图根据一元二次线性回归模型形成的曲线更契合散点图背后的趋势。

那么如何通过代码的方式来搭建一个一元二次线性回归模型呢，首先通过如下代码生成二次项数据：

from sklearn.preprocessing import PolynomialFeatures
poly_reg = PolynomialFeatures(degree=2)
X_ = poly_reg.fit_transform(X)

第1行代码引入增加一个多次项内容的模块：PolynomialFeatures；
第2行代码设置最高次项为二次项，为了下面生成x^2做准备；
第3行代码将原有的X转为一个新的二维数组X_，该二维数组包含新生成的二次项数据（x^{2）和原来一次项数据（x）。感兴趣的读者可以将X_打印出来看下，其效果为下图所示的一个二维数组，其中第一列数据为常数项数据1（其实就是x的0次方：x}0），没有特殊含义，不会产生影响；第二列数据为原来的一次项数据（其实就是x的1次方：x^{1）；第三列数据为生成的二次项数据（其实就是x的2次方：x}2），也即新生成的x^2集合。

生成完二次项数据后，就可以根据和之前一样的代码获得一元二次线性回归模型了：

regr = LinearRegression()
regr.fit(X_, Y)

然后通过和类似的代码就可以绘制上面的曲线图了，注意此时的predict()函数中填的是X_。

plt.scatter(X,Y)
plt.plot(X, regr.predict(X_), color='red')
plt.show()

通过类似的手段，我们可以获取此时的一元二次回归方程的系数a,b和常数项c，代码如下：

print(regr.coef_)  # 获取系数a, b 
print(regr.intercept_)  # 获取常数项c

结果如下：

[   0.         -743.68080444  400.80398224]
13988.159332096873

此时的系数项中为3个数，第一个0对应之前生成的X_常数项前面的系数，也对应之前说的X_的常数项不会产生影响；-743.68代表的X_一次项前面的系数，也即系数b；400.8代表的X_二次项前面的系数，也即系数a；而13988则代表常数项c，所以该一元二次线性回归方程为：

y = 400.8*x^2 - 743.68*x + 13988

用同样的方法，我们可以获取到金融行业、汽车制造行业、餐饮服务行业的工龄与薪酬的线性相关性，这四个行业的一元二次线性回归模型如下图所示：


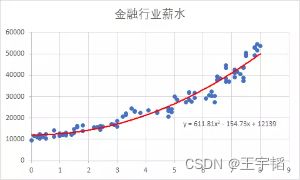
从上面四幅图可以看出，目前来说IT行业和金融行业的发展性较强，在工作一段时间后上升空间较大，汽车制造业和餐饮服务业则相对较弱，不过这些数据只是基于各行业100人的数据，所以得出来的结论仅供参考。

3.2 线性回归模型评估

模型搭建完成后，我们还需要对模型进行评估，这里我们主要以三个值作为评判标准：R-squared（也即统计学中常说的R^2）、Adj. R-squared（也即Adjusted R^2）、P值。其中R-squared和Adj. R-squared用来衡量线性拟合的拟合程度，P值用来衡量特征变量的显著性。

3.2.1 模型评估的编程实现

因为模型评估的数学原理相对比较复杂，而本书旨在以案例实战为主，数学推导为辅，所以这里先讲解在实战中如何对这些模型进行评估，然后再讲相关数学原理供感兴趣的读者参考。
在实战应用角度，我们只需要记得R squared或者Adj. R-squared越高，那么模型的拟合程度越高；如果P值越低，那么该特征变量的显著性越高，也即真的和预测变量有相关性。（R-squared和Adj. R-squared的取值范围为0-1；P值本质是个概率值，其取值范围也为0-1。）
在Python中，通过如下代码即可查看这三个参数：

import statsmodels.api as sm
X2 = sm.add_constant(X)
est = sm.OLS(Y, X2).fit()
print(est.summary())  # Jupyter Notebook中可以直接写est.summary()进行打印

其中第1行代码引入线性回归模型评估相关库：statsmodels库并简写为sm；

第2行代码通过add_constant()函数给原来的特征变量X添加常数项，并赋值为X2，这样才有y=ax+b中的常数项，也即截距b，注意之前的Scikit-learn库不需要这一步骤；
第3行代码通过OLS()及fit()函数对Y和X2进行线性回归方程搭建；
第四行代码则打印输出该模型的数据信息，如下图所示：

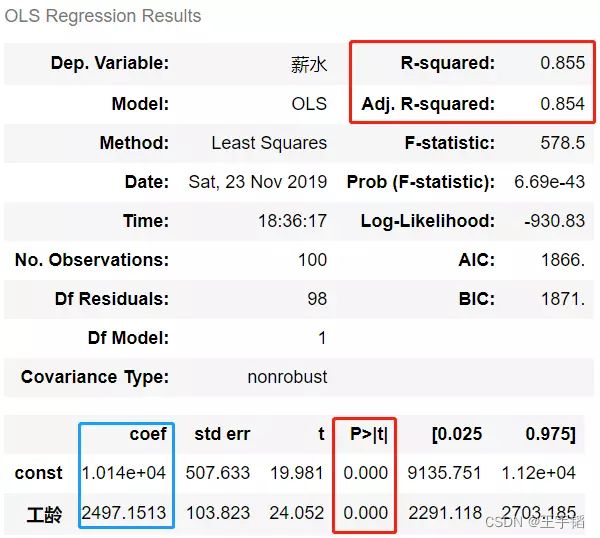
首先提一句，左下角的coef就是常数项和特征变量前的系数，也即截距b和斜率系数a，可以看到和之前求得的内容也是一致的。
对于模型评估而言，通常需要关心上图框中的R-squared、Adj. R-squared和P值信息。这里的R-squared为0.855，Adj. R-squared为0.854，说明模型的线性拟合程度较高；这里的P值有两个，常数项（const）和特征变量（工龄）的P值都约等于0，所以这两个变量都是和预测变量（薪酬）显著相关的，也即真的具有相关性，而不是由于偶然因素导致的。
感兴趣的读者也可以根据3.1.3节的补充知识点设置成一元二次方程，来看下模型评估效果，代码如下：

from sklearn.preprocessing import PolynomialFeatures
poly_reg = PolynomialFeatures(degree=2)
X_ = poly_reg.fit_transform(X)

import statsmodels.api as sm
X2 = sm.add_constant(X_)  # 这里传入的是含有x^2的X_
est = sm.OLS(Y, X2).fit()
est.summary() # 在非Jupyter Notebook的编辑器中需要写成print(est.summary())

此时打印结果获得的R-squared为0.931，的确相较于之前的0.855有所提升。

补充知识点：另一种获取R-squared值的代码实现
上面是通过引入线性回归模型评估相关库：statsmodels库来对线性回归模型来进行评估，那么有没有一个更通用的方法来获取R-squared值呢，因为我们将在第9章利用GBDT模型，第10章利用XGBoost和LightGBM模型来进行回归分析，此时便需要一个更加通用的获取R-squared值的方法，代码如下：

from sklearn.metrics import r2_score
r2 = r2_score(Y, regr.predict(X))

其中Y为真实值，regr.predict(X)为预测值，将r2打印，结果为0.855，可以看到和之前通过statsmodels库评估的结果是一致的。

3.2.2 模型评估的数学原理

上面我们演示了如果通过Python来查看R-squared值、Adj. R-squared值和P值，下面我们就来从数学原理的角度来讲解下这三个值是什么，供感兴趣的读者参考。

1.R-squared的理解
首先来看R-squared，要想理解R-squared，得先了解三个新的概念：整体平方和TSS(Total Sum of Squares)、残差平方和RSS(Residual Sum of Squares)、解释平方和ESS(Explained Sum of Squares)，为方便理解，相关的内容解释都绘制在下图中，其中Yi为实际值，Yfitted为预测值，Ymean为所有散点的平均值（为图片简洁，散点未绘制在其中）。

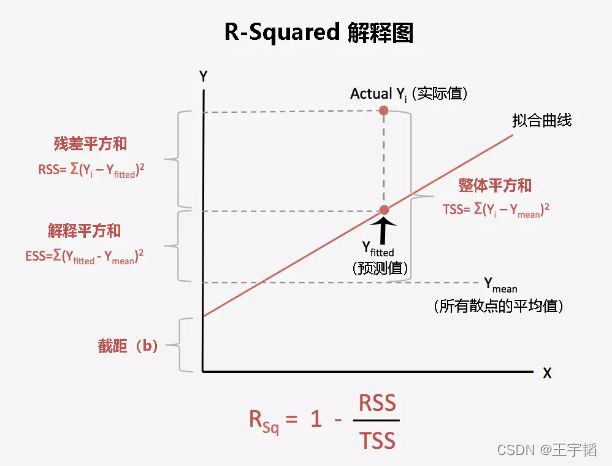
如上图所示，R-squared的公式为：1 - RSS/TSS，对于一个拟合程度较高的线性回归模型，我们希望其实际值尽可能的落在拟合曲线上，也即残差平方和RSS尽可能的小，也即R-squared尽可能的大。当RSS趋向于0的时候，说明实际值基本都落在了拟合曲线上，其拟合程度非常高，那么此时R-squared趋向于1，所以在实战当中，R-squared越大（越接近1），其拟合程度越高。不过也不是拟合程度越高越好，当拟合程度过高的时候，可能会导致过拟合的现象（关于过拟合的相关内容可以查看本小节的补充知识点）。
举例来说，对于以下数据

我们在3.1.1节演示过其拟合方程为y = x + 2，如下图所示：

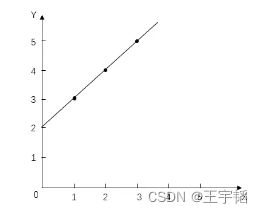
其中所有散点的平均值，在本演示案例中，因为数据较少且拟合程度好，所以预测值= Yi。如下所示，将数据代入得到各平方和，从而得到R-squared值。

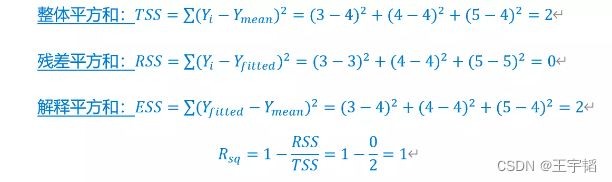
这里的R-squared值为1，也即完全拟合。此外，我们可以看到，也即残差平方和+解释平方和=整体平方和，这个也的确符合我们在原理图中展示的内容。

补充知识点：过拟合与欠拟合
如下图所示，所谓过度拟合（简称过拟合），是指模型在训练样本中拟合程度过高，虽然它很好地贴合了训练集数据，但是却丧失了泛化能力，模型不具有推广性（即如果换了训练集以外的数据就达不到较好的预测效果），导致在新的数据集中表现不佳。此外与过拟合相对的则是欠拟合，欠拟合是指模型拟合程度不高，数据距离拟合曲线较远，或指模型没有很好地捕捉到数据特征，不能够很好地拟合数据。

2.Adj. R-squared的理解
Adj. R-squared是R-squared的改进版，其目的是为了防止选取的特征变量过多（主要针对下一节将讲到的多元线性回归），而导致虚高的R-squared。每当新增一个特征变量的时候，因为线性回归背后的数学原理，都会导致R-squared增加，但是可能这个新增的特征变量可能对模型并没有什么帮助，为了限制过多的特征变量，所以引入了Adj. R-squared的概念，它会在原来R-squared的基础上额外考虑到特征变量数目这一值，其公式如下：

其中n为样本数量，k为特征变量数量，可以看到当特征变量数量k越多的时候，其实会对Adj. R-squared产生负影响，因此不要为了一味地追求高R-squared而过多的添加特征变量。所以当考虑了特征变量数量后，Adj. R-squared能够更加准确地反映线性模型的拟合程度。
举例来说，对于在上一小节R-squared中的举的例子而言，其Adj. R-squared的计算过程与结果如下所示：

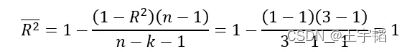
可以看到对于完全拟合的线性方程，Adj. R-squared和R-squared是一致的，都为数字1。倘若不是完全拟合，例如此时的R-squared为0.9，那么此时Adj. R-squared的计算过程与结果如下所示：

可以看到此时的Adj. R-squared的确小于R-squared。

3.P值的理解
P值涉及统计学里假设检验中的概念，
其原假设为特征变量与预测变量无显著相关性，
P值是当原假设为真时所得到的样本观察结果或更极端结果出现的概率。
如果该概率越大，也即P值越大，原假设为真的可能性就越大，也即无显著相关性的可能性越大；
如果该概率越小，也即P值越小，原假设为真的可能性就越小，也即有显著相关性的可能性越大，所以P值越小，显著相关性越大。
通常来说，我们会以0.05为阈值，当P值小于0.05时，就认为该特征变量与预测变量显著相关，P值越大，表示自变量和因变量没什么关系。

在下一章：逻辑回归模型4.2.3节中我们还将介绍通过划分测试集和训练集的方式来评估模型的预测效果。

3.3 多元线性回归

多元线性回归的本质原理和一元线性回归是一样的，不过因为多元线性回归可以考虑到多个因素对预测变量的影响，所以在商业实战中应用更为广泛。

3.3.1 多元线性回归的数学原理和代码实现

多元线性回归模型的原理其实和一元线性回归的原理类似，其形式可以用如下公式表达：

y = k0 + k1*x1 + k2*x2 + k3*x3……

其中x1、x2、x3……为不同特征变量，k1、k2、k3……则为这些特征变量前的系数，k0为常数项，多元线性回归模型的搭建也是通过数学计算来获取合适的系数，使得下图所示的残差平方和最小，其中为实际值，为预测值。

在数学上我们通过最小二乘法和梯度下降法来对系数进行求解，其具体步骤可参考3.1.1节的补充知识点，本节主要讲解如何通过Python代码实现。其核心代码和一元线性回归其实是一致的，代码如下。

from sklearn.linear_model import LinearRegression
regr = LinearRegression()
regr.fit(X,Y)

上面代码和一元线性回归的代码的区别在于这里的X是包含多个特征变量信息的。利用多元线性回归可以做很多更加丰富的案例，比如通过工龄、地域、行业等因素来预测收入情况，通过房屋大小、所处位置、是否临近地铁等因素来预测房价等。下一小节我们将讲解一个在银行业比较常见的模型，通过多元线性回归模型来预测客户的价值。

3.3.2 案例实战：客户价值预测模型

利用多元线性回归模型我们可以根据多个因素对客户的价值进行预测，当模型搭建完成后，便可以对不同价值的客户构建不同的业务策略。

1.案例背景
这里以信用卡客户的客户价值来解释下客户价值预测的具体含义：客户价值预测就是指客户未来一段时间能带来多少利润，其利润的来源可能来自于信用卡的年费、取现手续费、分期手续费、境外交易手续费用等。而分析出客户的价值后，在进行营销、电话接听、催收、产品咨询等各项服务时，就可以针对高价值的客户进行区别于普通客户的服务，有助于进一步挖掘这些高价值客户的价值，并提高这些高价值客户的忠诚度。

2.读取数据
通过如下代码读取相关数据，这里共选取了100多组已有的客户价值数据，其中一些数据已经经过一些简单预处理了。

import pandas
df = pandas.read_excel('客户价值数据表.xlsx')
df.head()  # 显示前5行数据

此时数据如下，有几个注意点：其中客户价值为1年的客户价值，即在1年里能给银行带来的收益；学历已经进行数据的预处理，其中2表示高中学历，3表示本科学历，4表示研究生学历；性别中0表示女，1表示男（数据预处理的相关知识点可以参考本书第11章）。

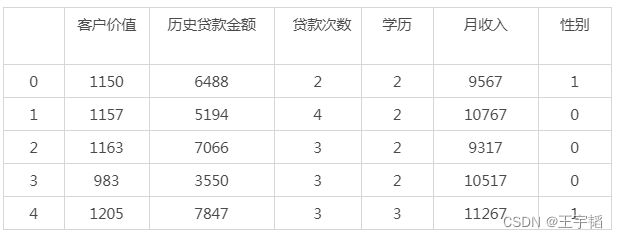
此时的后5列为自变量 ，“客户价值”为因变量，通过如下代码进行自变量、因变量选取：

X = df[['历史贷款金额', '贷款次数', '学历', '月收入', '性别']]
Y = df['客户价值']

这里的自变量X同样必须写成二维数据结构，在这里就更加容易理解了，因为它需要包含多个特征变量；而因变量Y写成一维的数据结构即可。

3.模型搭建
根据3.1.2小节中的知识点，通过如下代码即可搭建线性回归模型：

from sklearn.linear_model import LinearRegression
regr = LinearRegression()
regr.fit(X,Y)

4.线性回归方程构造
我们还可以通过上一小节的知识点查看该直线的斜率系数a和截距b，代码如下：

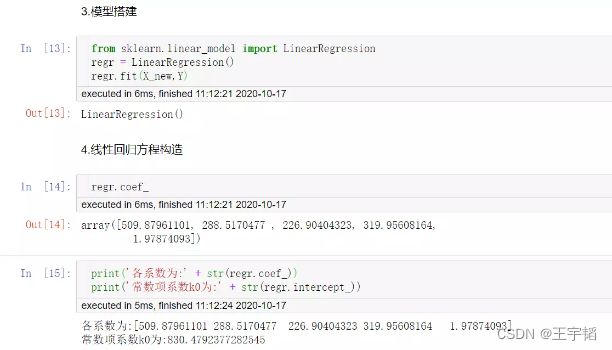
print('各系数为:' + str(regr.coef_))
print('常数项系数k0为:' + str(regr.intercept_))

运行结果如下：

各系数为:[5.71421731e-02 9.61723492e+01 1.13452022e+02 5.61326459e-02
 1.97874093e+00]
常数项系数k0为:-208.4200407997355

其中这里通过regr.coef_获得是一个系数列表，分别对应不同特征变量前面的系数，也即k1、k2、k3、k4及k5，所以此时的多元线性回归曲线方程为：

y = -208 + 0.057*x1 + 96*x2 + 113*x3 + 0.056*x4 + 1.97*x5

完整代码如下所示：

# 1.读取数据
import pandas
df = pandas.read_excel('客户价值数据表.xlsx')
df.head()
X = df[['历史贷款金额', '贷款次数', '学历', '月收入', '性别']]
Y = df['客户价值']

# 2.模型训练
from sklearn.linear_model import LinearRegression
regr = LinearRegression()
regr.fit(X,Y)

# 3.线性回归方程构造
print('各系数为:' + str(regr.coef_))
print('常数项系数k0为:' + str(regr.intercept_))

5.模型评估
利用3.2节模型评估的方法我们也可以对多元线性回归进行模型评估，代码如下：

import statsmodels.api as sm  # 引入线性回归模型评估相关库
X2 = sm.add_constant(X)
est = sm.OLS(Y, X2).fit()
print(est.summary())

此时运行结果如下图所示：

可以看到模型整体的R-squared为0.571，Adj. R-Squared为0.553，整体拟合效果不是特别好，可能是因为数据量偏少的原因，不过在现有的数据量条件下也可以接受。同时我们再来观察P值，可以发现大部分特征变量的P值都较小，的确是和预测变量：客户价值显著相关，而性别这一特征变量的P值达到了0.951，即与预测变量没有显著相关性，这个也的确符合经验认知，所以在之后的建模当中，我们其实可以把性别这一特征变量舍去。
此外，这里是知道客户的客户价值从而进行的建模，如果我们不知道客户价值（也即不知道预测变量），那便属于非监督式机器学习了，此时便不能直接对客户的价值进行预测，不过我们可以利用本书第13章的相关知识点对客户进行分群，感兴趣的读者可以先行翻阅。

至此多元线性回归模型的讲解便告一段落了，关于多元线性回归还有很多值得探讨的地方，例如如何进行数据预处理以及解决多重共线性等以及过拟合问题，这个我们将在第11章：特征工程之数据预处理进行讲解讲解。线性回归模型的优点在于其可解释性很强而且建模速度较快，其缺点在于模型相对简单，而且主要针对线性数据，局限性较大。在真正的商业实战中，线性回归模型应用相对不那么多，我们还将在第9章和第10章讲解如何通过集成模型：GBDT、XGBoost、LightGBM模型来进行回归预测模型，所以这里对于线性回归模型做一个简单的了解即可，可以当做机器学习的一个入门知识点。

3.3.3 特征重要性挖掘

from sklearn.preprocessing import MinMaxScaler
X_new = MinMaxScaler().fit_transform(X)
X_new

补充：3.3.4 划分测试集和训练集数据

补充知识点

1.Python解常规方程

https://www.cnblogs.com/ty123/p/10529541.html
解一元三次方程

import sympy as sp
x = sp.Symbol('x')
f = x**3 + 2*x**2-1
res = sp.solve(f)

此时res就是求解结果，res是一个列表，里面有3个解，如下所示：

[-1, -1/2 + sqrt(5)/2, -sqrt(5)/2 - 1/2]

如果想看整数或者小数，可以用int()或者float()函数：

float(res[1])  # 打印第二个解

获取结果如下：

0.6180339887498949

如果想保留两位小数，可以通过round函数，进行小数位保留，代码如下：

round(float(res[1]), 2)

获取结果如下，可以用print()函数将其打印：

0.62

其余常规方程，可以参考上面的第一条链接，它还可以求解多元方程。

2.Python数据拟合及求函数表达式

https://blog.csdn.net/changdejie/article/details/83089933

2.1 方式1：多项式拟合

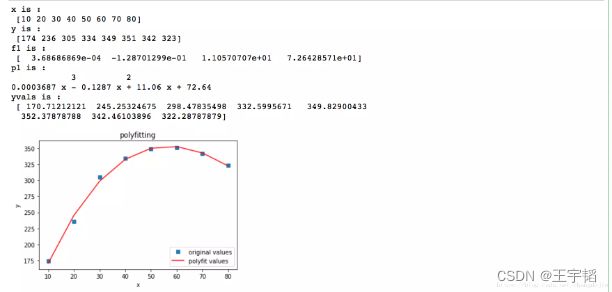
1.第一种是进行多项式拟合，数学上可以证明，任意函数都可以表示为多项式形式。具体示例如下。

import numpy as np
import matplotlib.pyplot as plt

# 定义x、y散点坐标
x = [10,20,30,40,50,60,70,80]
x = np.array(x)
print('x is :\n',x)
num = [174,236,305,334,349,351,342,323]
y = np.array(num)
print('y is :\n',y)
# 用3次多项式拟合
f1 = np.polyfit(x, y, 3)
print('f1 is :\n',f1)

p1 = np.poly1d(f1)
print('p1 is :\n',p1)

# 也可使用yvals=np.polyval(f1, x)
yvals = p1(x)  # 拟合y值
print('yvals is :\n',yvals)
# 绘图
plot1 = plt.plot(x, y, 's',label='original values')
plot2 = plt.plot(x, yvals, 'r',label='polyfit values')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc=4)  # 指定legend的位置右下角
plt.title('polyfitting')
plt.show()

得到结果如下：

2.2 方式2：具体函数拟合

2.第二种方案是给出具体的函数形式(可以是任意的，只要你能写的出来 下面的func就是)，用最小二乘的方式去逼近和拟合，求出函数的各项系数，如下，其中sqrt求开方，即根号x，square即求平方，即平方x，如果想用幂函数，用**，例如2**3=8。

# 使用curve_fit

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

# 自定义函数 e指数形式
def func(x, a, b,c):
    return a*np.sqrt(x)*(b*np.square(x)+c)

# 定义x、y散点坐标
x = [20,30,40,50,60,70]
x = np.array(x)  # 其实不需要转成numpy格式，练习题验证了
num = [453,482,503,508,498,479]
y = np.array(num)

# 非线性最小二乘法拟合
popt, pcov = curve_fit(func, x, y)
# 获取popt里面是拟合系数
print(popt)
a = popt[0]
b = popt[1]
c = popt[2]
yvals = func(x,a,b,c)  # 拟合y值
print('popt:', popt)
print('系数a:', a)
print('系数b:', b)
print('系数c:', c)
print('系数pcov:', pcov)
print('系数yvals:', yvals)
# 绘图
plot1 = plt.plot(x, y, 's',label='original values')
plot2 = plt.plot(x, yvals, 'r',label='polyfit values')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc=4)  # 指定legend的位置右下角
plt.title('curve_fit')
plt.show()

生成结果如下：

练习题：Python四参数Logistic拟合

有如下数据

X = [0.13, 0.18, 0.24, 0.32, 0.42, 0.56, 0.75]
Y = [49.78, 49.48, 48.79, 47.22, 43.90, 37.69, 28.42]

求方程：y=(a-d)/(1+(x/c)^b)+d 中的a,b,c,d

答案：

# 使用curve_fit
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

# 自定义函数 
def func(x, a, b, c, d):
    return (a-d)/(1+(x/c)**b)
    
# 测试数据1
x = [0.13, 0.18, 0.24, 0.32, 0.42, 0.56, 0.75]
y = [49.78, 49.48, 48.79, 47.22, 43.90, 37.69, 28.42]

# 非线性最小二乘法拟合
popt, pcov = curve_fit(func, x, y)
# 获取popt里面是拟合系数
print(popt)
a = popt[0]
b = popt[1]
c = popt[2]
d = popt[3]
yvals = func(x, a, b, c, d)  # 拟合y值
print('popt:', popt)
print('系数a:', a)
print('系数b:', b)
print('系数c:', c)
print('系数d:', d)
print('系数pcov:', pcov)
print('系数yvals:', yvals)
# 绘图
plot1 = plt.plot(x, y, 's',label='original values')
plot2 = plt.plot(x, yvals, 'r',label='polyfit values')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc=4)  # 指定legend的位置右下角
plt.title('curve_fit')
plt.show()

获取结果如下所示：

如果测试数据如下，则可以换成相关数据：

# 测试数据2
x = [900, 300, 100, 33.3, 11.1, 3.7, 1.23, 0]
y = [4.2, 3.994, 3.3865, 1.8915, 0.7275, 0.302, 0.143, 0.066]

获取结果如下所示：

练习题：模型评估

通过如下代码可以计算R^2，也即回归模型的拟合度，代码如下：

from sklearn.metrics import r2_score
r2 = r2_score(y, yvals)

打印r2得到拟合度如下所示：

0.9996809509783059

点击下载。

3.4课程相关资源

笔者获取方式：微信号获取

添加如下微信：huaxz001 。

笔者网站：www.huaxiaozhi.com

王宇韬相关课程可通过：
京东链接：[https://search.jd.com/Search?keyword=王宇韬]，搜索“王宇韬”，在淘宝、当当也可购买。加入学习交流群，可以添加如下微信：huaxz001（请注明缘由）。

各类课程可在网易云、51CTO搜索王宇韬，进行查看。