python实现四边形IoU计算
计算两个矩形的交并比,通常在检测任务里面可以作为一个检测指标。预测bbox和groundtruth之间的差异,可以通过IoU来体现。
1.平齐矩形IoU计算
交并比:(Intersection over Union)
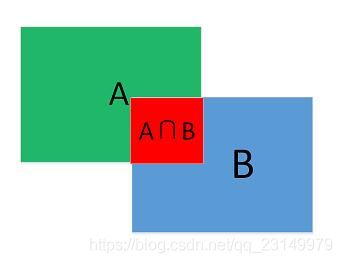
如上图所示,IOU值定位为两个矩形框面积的交集和并集的比值。即:
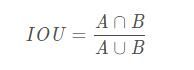
交并比的实现也是非常简单的,执行过程如下:
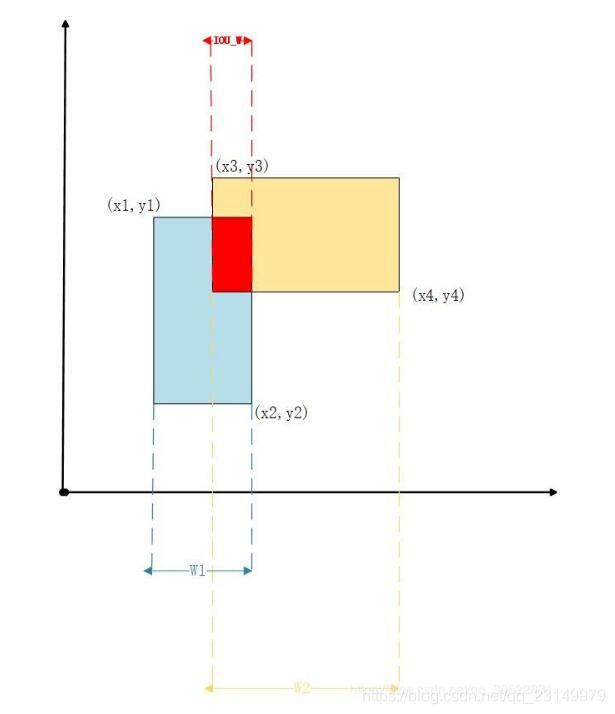
交集形状的宽度计算为:IOU_W = min(x1,x2,x3,x4)+w1+w2-max(x1,x2,x3,x4)
交集形状的高度计算为:IOU_H = min(y1,y2,y3,y4)+h1+h2-max(y1,y2,y3,y4)
代码实现如下:
getIoU.py
#!/usr/bin/env python
# encoding: utf-8
# 创建求IoU的类
class getIoU(object):
# 计算平齐矩形IoU
def getrectiou(self,rec1, rec2):
"""
computing IoU
:param rec1: (y0, x0, y1, x1), which reflects
(top, left, bottom, right)
:param rec2: (y0, x0, y1, x1)
:return: scala value of IoU
"""
# computing area of each rectangles
S_rec1 = (rec1[2] - rec1[0]) * (rec1[3] - rec1[1])
S_rec2 = (rec2[2] - rec2[0]) * (rec2[3] - rec2[1])
# computing the sum_area
sum_area = S_rec1 + S_rec2
# find the each edge of intersect rectangle
left_line = max(rec1[1], rec2[1])
right_line = min(rec1[3], rec2[3])
top_line = max(rec1[0], rec2[0])
bottom_line = min(rec1[2], rec2[2])
# judge if there is an intersect
if left_line >= right_line or top_line >= bottom_line:
return 0
else:
intersect = (right_line - left_line) * (bottom_line - top_line)
return (intersect / (sum_area - intersect)) * 1.0
if __name__ == '__main__':
rect1 = (661, 27, 679, 47)
# (top, left, bottom, right)
rect2 = (662, 27, 682, 47)
iou = getIoU().getrectiou(rect1, rect2)
print(iou)
以上内容来源于网络!
2.四边形IoU计算
本节介绍不规则区域的IoU计算,以四边形IoU计算为例。

给出目标1、2的顶点坐标:
quadrangle1=[qr1x1, qr1y1, qr1x2, qr1y2, qr1x3, qr1y3, qr1x4, qr1y4]
quadrangle2=[qr2x1, qr2y1, qr2x2, qr2y2, qr2x3, qr2y3, qr2x4, qr2y4]
算法思路:
(1)根据坐标信息,选取有效工作区域;
(2)对有效区域进行检索,分别计算出并集部分和交集部分;
(3)计算得出IoU。
程序getqrIoU.py如下:
#!/usr/bin/env python
# encoding: utf-8
import isPointInRect
# 创建求IoU的类
class getIoU(object):
# 计算四边形IoU
def getqriou(self, quadrangle1, quadrangle2):
# quadrangle1 = [qr1x1, qr1y1, qr1x2, qr1y2, qr1x3, qr1y3, qr1x4, qr1y4]
# quadrangle2=[qr2x1, qr2y1, qr2x2, qr2y2, qr2x3, qr2y3, qr2x4, qr2y4]
intersection = 0
union = 0
# find the each edge of intersect rectangle
left_line = min(quadrangle1[0][0], quadrangle1[1][0], quadrangle1[2][0], quadrangle1[3][0],
quadrangle2[0][0], quadrangle2[1][0], quadrangle2[2][0], quadrangle2[3][0])
right_line = max(quadrangle1[0][0], quadrangle1[1][0], quadrangle1[2][0], quadrangle1[3][0],
quadrangle2[0][0], quadrangle2[1][0], quadrangle2[2][0], quadrangle2[3][0])
top_line = min(quadrangle1[0][1], quadrangle1[1][1], quadrangle1[2][1], quadrangle1[3][1],
quadrangle2[0][1], quadrangle2[1][1], quadrangle2[2][1], quadrangle2[3][1])
bottom_line = max(quadrangle1[0][1], quadrangle1[1][1], quadrangle1[2][1], quadrangle1[3][1],
quadrangle2[0][1], quadrangle2[1][1], quadrangle2[2][1], quadrangle2[3][1])
validregion_w, validregion_h = abs(right_line - left_line), abs(bottom_line - top_line)
print("有效区域的宽:",validregion_w," 高:", validregion_h)
print("有效区域大小:",validregion_w* validregion_h)
for i in range(int(validregion_h)):
for j in range(int(validregion_w)):
x = left_line + j
y = top_line + i
point = [x,y]
flag1 = isPointInQuadrangle(point, quadrangle1)
flag2 = isPointInQuadrangle(point, quadrangle2)
if flag1:
if flag2:
intersection += 1
union += 1
else:
intersection += 1
else:
if flag2:
intersection += 1
else:
continue
print("交集:", intersection," 并集:", union)
if intersection != 0:
iou = union / intersection
else:
iou = 0
return iou
if __name__ == '__main__':
quadrangle1 = [[600, 400], [800, 680], [500, 600], [900, 460]]
# quadrangle2 = [[560, 750], [700, 580], [860, 820], [980, 700]]
quadrangle2 = [[600, 400], [800, 680], [500, 600], [900, 460]]
iou = getIoU().getqriou(quadrangle1, quadrangle2)
print(iou)
输出信息为:
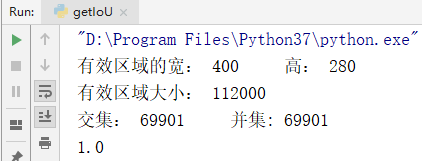
表示完全重叠。
isPointInRect函数可采用其他算法,一种算法请参考本文。对于多边形IoU计算,只要更改此处相应的算法便可实现,本例不再赘述。
因编写时间仓促,如有问题请反馈!
另外,其他资料提供了“利用polygon计算多边形IOU”的方法,请查阅其他资料。