Matlab语音及音乐信号的采集、滤波
电信19-2 翁大弟
一、实验目的
1、 理解采样率和量化级数对语音信号的影响;
2、 设计滤波器解决实际问题。
二、实验原理
(1)观察使用不同采样率及量化级数所得到的信号的听觉效果,从而确定对不同信号的最佳的采样率;
(2)分析音乐信号的采样率为什么要比语音的采样率高才能得到较好的听觉效果;
(3)注意观察信号中的噪声(特别是50hz交流电信号对录音的干扰,设计一个滤波器去除该噪声。
三、实验提示
(1)推荐录音及播放软件
(2)分析语音及音乐信号的频谱,根据信号的频率特性理解采样定律对信号数字化的工程指导意义;
(3)可用带阻滤波器对50Hz交流电噪声进行去噪处理;
(4)也可研究设计自适应滤波器对50Hz噪声及其它随机环境噪声进行滤波处理。
MATLAB简介
MATLAB是由美国Mathwork公司开发的数值计算、符号计算和图形可视化三大基本功能于一体,功能强大、操作简单的语言。是国际公认的优秀数学应用软件之一。
现在,MATLAB已经发展成为适合多学科的大型软件,在世界各高校,MATLAB已经成为线性代数、数值分析、数理统计、优化方法、自动控制、数字信号处理、动态系统仿真等高级课程的基本教学工具。特别是最近几年,MATLAB在我国大学生数学建模竞赛中的应用,为参赛者在有限的时间内准确、有效地解决问题提供了有力的保证。
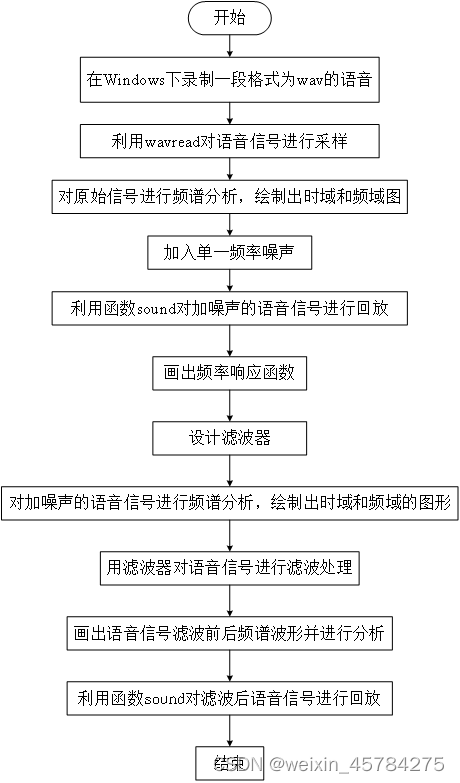
四、设计流程
采集一段音乐信号。将音乐信号的文件名命名为input.wav,再用MATLAB中的wavread函数求出语音信号的三个参数:每个样本的值、生成该音乐波形文件时的采样频率和波形文件样本的码数,再对信号及加入单频干扰后的音乐信号做傅立叶变化,绘制出时域和频域的波形。最后通过滤波绘制滤波前后时域波形对比图和幅频特性对比图,并回放滤波前后的音乐信号来验证是否达到去噪的目的。
(图1设计流程图)
五、实验源码及结果分析
5.1录制音乐信号
用windows工具中的录音机录制一段音乐信号,时间长度约为2s。将信号文件名设置为input.wav,并将文件保存在MATLAB下的WOK文件夹里面。然后在MATLAB平台上,用audioread函数调出此音乐信号,并得到其采样率fs。分别使用了8k,16k,32k三种采样率录制了三段语音信号,8k采样率的音乐明显少了许多频率成分,失真严重,高音部分基本听不到了,总之对于音乐信号,8k采样率太低不适合音乐的欣赏,16k采样率较8k来说频率成分丰富了很多,音乐更加优美动听,32k采样率在此基础上音质有所提升。
[x,fs]=audioread('input.wav') ; % 输入参数为文件的全路径和文件名,输出的第一个参数是信号的样本值,fs是生成该波形文件时的采样率,bits是波形文件每样本的编码位数。
sound(x,fs); % 按指定的采样率和每样本编码位数回放录音
x=x(:,2);
N=length(x); % 计算信号x的长度
fn=1000; % 单频噪声频率
t=0:1/fs:(N-1)/fs; % 计算时间范围,样本数除以采样频率
x=x';
y=x+0.1.*sin(fn*2*pi*t); %y为加入单频干扰信号后的音乐
sound(y,fs) ;在MATLAB平台上,
plot(t,x)
title('原始音乐信号')
xlabel('时间(s)')
ylabel('幅度')
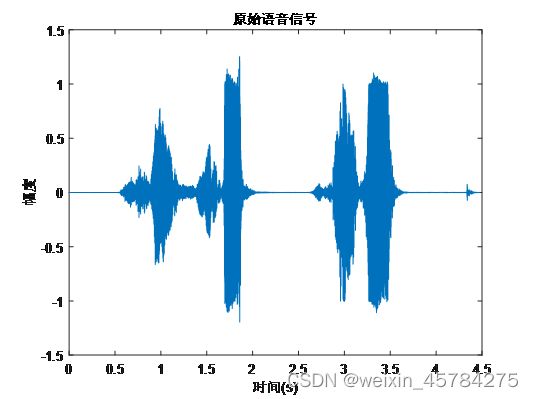
用plot函数画出原始语音信号,如图2所示:
图2 原始语音信号时域图
5.2对原信号加入噪声
在MATLAB平台上,对原始信号和加噪信号进行fft变换,取幅度谱,并对频谱进行分析。具体实现如下:
[x,fs]=audioread('input.wav'); % 输入参数为文件的全路径和文件名,输出的第一个参数是信号的样本值,fs是生成该波形文件时的采样率。
sound(x,fs); % 按指定的采样率和每样本编码位数回放录音
x=x(:,2);
N=length(x); % 计算信号x的长度
fn=1000; % 单频噪声频率
t=0:1/fs:(N-1)/fs; % 计算时间范围,样本数除以采样频率
x=x';
y=x+0.1.*sin(fn*2*pi*t); %y为加入单频干扰信号后的语音
sound(y,fs) ; % 对加噪信号进行回放
X=abs(fft(x));% 对原始信号进行fft变换,取幅度谱
Y=abs(fft(y)); % 对加噪后信号进行fft变换,取幅度谱
X=X(1:N/2); Y=Y(1:N/2); % 截取前半部分
deltaf=fs/N; % 计算频谱的谱线间隔
f=0:deltaf:fs/2-deltaf; % 计算频谱频率范围
subplot(2,2,1);
plot(t,x);
%axis([0 1 -1 1]); grid on; %画原始语音信号的时域图
xlabel('时间(s)');ylabel('幅度');title('原始语音信号');
subplot(2,2,2);plot(f,X);
%axis([0 4000 0 1500]);
grid on; %画原始语音信号幅度谱图
xlabel('频率(Hz)');ylabel('幅度谱');title('语音信号幅度谱图');
subplot(2,2,3);plot(t,y);
%axis([0 1 -1 1]); grid on; %画加噪语音信号的时域图
xlabel('时间(s)');ylabel('幅度'); title('加入单频干扰后的语音信号');
subplot(2,2,4);plot(f,Y);
%axis([0 4000 0 1500]);
grid on; %画加噪语音信号幅度谱图
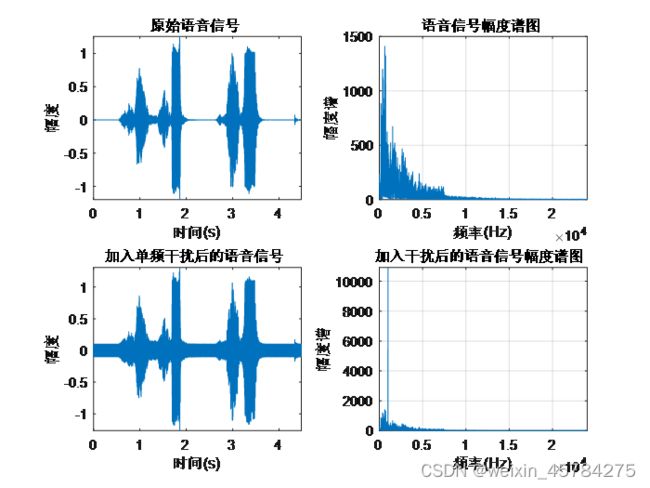
xlabel('频率(Hz)');ylabel('幅度谱');title('加入干扰后的语音信号幅度谱图');在MATLAB上运行结果如图3所示:
图3 原始信号及加噪信号的时域图及幅度谱图
由图3可以看出,对比原始信号与加噪信号幅度谱图我们可以清晰的看到在1000Hz是出现了一个脉冲,从而使原有的音频听上去有了噪声,这样就到达了预期结果。
分析可知:但是对于语音信号来说,8采样率用于通话交流系统已经足够了,采样率的提高对于音质的提升不大;对于音乐信号,8k采样率太低不适合音乐的欣赏,16k采样率较8k来说频率成分丰富了很多,音乐更加优美动听,32k采样率在此基础上音质有所提升。
5.3滤波器的设计
滤波器设计就是要找到一组能满足特定滤波要求的系数向量a和b,而它主要是通过设计指标来实现的。滤波器设计的要求或指标一般是在频域上给出的,常用的滤波器频域指标有:fp1、fs1、fs2、fp2、Rp、As。要达到最佳的滤波效果,则需要对fp1、fs1、fs2、fp2和Rp、As进行适当的调整。由图3-3可以看出,音乐信号可以选择fp1=900;fs1=950;fs2=1050;fp2=1100;Rp=1;As=60的滤波器。在MATLAB中,通常采用1/2采样频率进行归一化处理,如果将频率转化为角频率,则需将归一化频率乘以pi。设计程序如下:
fp1=900;fs1=950;fs2=1050;fp2=1100;Rp=1;As=60; % 带阻滤波器设计指标
fc1=(fp1+fs1)/2;fc2=(fp2+fs2)/2; df=min((fs1-fp1),(fp2-fs2)); % 计算上下边带中心频率,和频率间隔
wc1=fc1/fs*2*pi;wc2=fc2/fs*2*pi; dw=df/fs*2*pi; %将Hz为单位的模拟频率换算为rad为单位的数字频率
ws1=fs1/fs*2*pi;ws2=fs2/fs*2*pi;
M=ceil((As-7.95)/(2.285* dw)+1)+1; % 计算汉宁窗设计该滤波器时需要的阶数
n=0:M-1; beta=0.1102*(As-8.7); % 定义时间范围
w_kaiser= kaiser(M,beta); % 产生M阶的凯塞窗
hd_bs=ideal_lp(wc1,M)+ideal_lp(pi,M)-ideal_lp(wc2,M); % 调用自编函数计算理想带阻滤波器的脉冲响应
h_bs=w_kaiser'.*hd_bs; % 用窗口法计算实际滤波器脉冲响应
[db,mag,pha,grd,w]=freqz_m(h_bs,1); % 调用自编函数计算滤波器的频率特性
Rp=-min(db(wc1/dw+1:1:wc2/dw)); As=max(-round(db(ws2/dw+1:1:501)));
subplot(2,2,1);plot(w/pi,db);axis([0 0.2 -70 10]);
xlabel('w/pi');ylabel('dB');title('滤波器幅度响应图');grid on;
subplot(2,2,2);plot(w/pi,mag);axis([0 0.2 0 1.2]);
xlabel('w/pi');ylabel('幅度mag');title('滤波器幅度响应图');grid on;
subplot(2,2,3);plot(w/pi,pha);axis([0 1 -3 3]);
xlabel('w/pi');ylabel('相位pha');title('滤波器相位响应图');grid on;
subplot(2,2,4);stem(n,h_bs);axis([0 1500 0 1]);
xlabel('n');ylabel('h(n)');title('滤波器脉冲响应图');grid on;
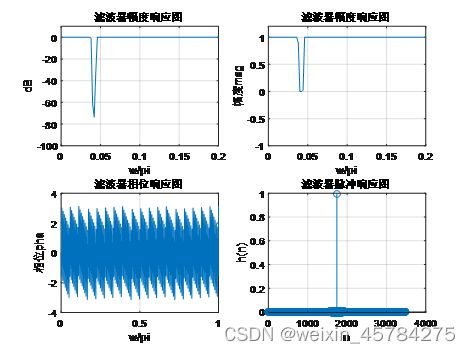
所设计的滤波器的幅度响应和脉冲响应如图4所示:
由图4可以看出Rp接近于0,而As大于开始的设定值(As=60db)。
5.4信号的滤波处理
滤波器设计完成后,在MATLAB平台上调用函数fftfilt对信号实现滤波,绘制音乐信号去噪前后时域图,频域幅度图形并进行比较。具体程序如下:
y_fil=fftfilt (h_bs, y); % 用设计好的滤波器对y进行滤波
Y_fil=fft(y_fil);Y_fil=Y_fil(1:N/2); % 计算频谱取前一半
subplot(3,2,1);plot(t,x); %axis([0 3 -0.2 0.2]);
xlabel('时间(s)');ylabel('幅度');title('原始音乐信号x');grid on;
subplot(3,2,2);plot(f,X);%axis([0 4000 0 70]);
xlabel('频率(Hz)');ylabel('幅度谱');title('音乐信号幅度谱X');grid on;
subplot(3,2,3);plot(t,y);% axis([0 3 -0.2 0.2]);
xlabel('时间(s)');ylabel('幅度');title('加干扰后的音乐信号x1');grid on;
subplot(3,2,4);plot(f,Y);%axis([0 4000 0 70]);
xlabel('频率(Hz)');ylabel('幅度谱');title('加干扰音乐信号幅度谱X1');grid on;
subplot(3,2,5);plot(t,y_fil);%axis([0 3 -0.2 0.2])
xlabel('时间(s)');ylabel('幅度');title('滤波后音乐信号y');grid on;
subplot(3,2,6);plot(f,Y_fil); %axis([0 4000 0 70])
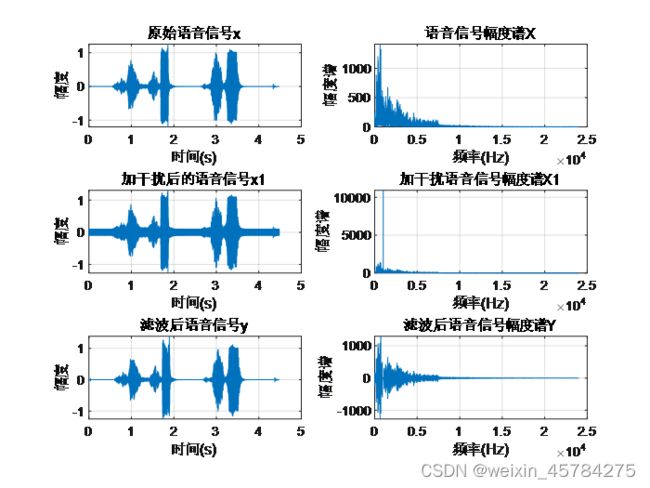
xlabel('频率(Hz)');ylabel('幅度谱');title('滤波后音乐信号幅度谱Y');grid on;
sound (y_fil,fs)
图5 语音信号去噪前后时域图及频域幅度图
六、实验结论和心得
对于语音信号,采用8kHz的采样率,8位量化电平数已经足以进行语音交流,而对于音乐信号,由于频率范围较大,最好能达到16khz以上的采样率,量化电平16bit足够了。
现在的电脑电源滤波效果较好,录音频谱中50Hz的交流噪声分量很小,所以演示时为了体现陷波器的效果,需要额外混进50Hz的正弦波噪声进行演示;陷波器本质是滤波器,其过渡带大小会影响到周围频谱分量的大小,能够观察到进行50Hz陷波后其周围频率分量均有降低。人工混进噪声频率后,其他频率分量大小均有变化,所以特定频率的噪声也会对整体的语音效果造成影响。
这次实验进一步加深了我对语音信号的了解,和熟练了对Matlab的使用,让我对信号处理这门课程有了更加浓厚的兴趣。因为以前都是基于课本上所学的理论知识,然而通过这次课程设计之后才能真正理解其意义。这次课程设计使我了解了MATLAB的使用方法,学会分析滤波器的优劣和性能,提高了分析和动手实践能力,同时我相信,进一步加强对MATLAB的学习与研究对我今后的学习将会起到很大的帮助!
搜索
复制