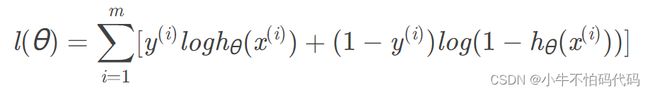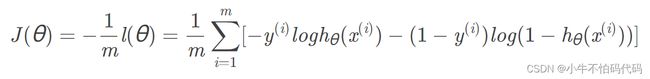吴恩达《机器学习》ex2作业第一部分Python实现——逻辑回归 参考

Programming Exercise 2 :Logistic Regression

逻辑回归

一、所用数据集：

34.62365962451697,78.0246928153624,0
30.28671076822607,43.89499752400101,0
35.84740876993872,72.90219802708364,0
60.18259938620976,86.30855209546826,1
79.0327360507101,75.3443764369103,1
45.08327747668339,56.3163717815305,0
61.10666453684766,96.51142588489624,1
75.02474556738889,46.55401354116538,1
76.09878670226257,87.42056971926803,1
84.43281996120035,43.53339331072109,1
95.86155507093572,38.22527805795094,0
75.01365838958247,30.60326323428011,0
82.30705337399482,76.48196330235604,1
69.36458875970939,97.71869196188608,1
39.53833914367223,76.03681085115882,0
53.9710521485623,89.20735013750205,1
69.07014406283025,52.74046973016765,1
67.94685547711617,46.67857410673128,0
70.66150955499435,92.92713789364831,1
76.97878372747498,47.57596364975532,1
67.37202754570876,42.83843832029179,0
89.67677575072079,65.79936592745237,1
50.534788289883,48.85581152764205,0
34.21206097786789,44.20952859866288,0
77.9240914545704,68.9723599933059,1
62.27101367004632,69.95445795447587,1
80.1901807509566,44.82162893218353,1
93.114388797442,38.80067033713209,0
61.83020602312595,50.25610789244621,0
38.78580379679423,64.99568095539578,0
61.379289447425,72.80788731317097,1
85.40451939411645,57.05198397627122,1
52.10797973193984,63.12762376881715,0
52.04540476831827,69.43286012045222,1
40.23689373545111,71.16774802184875,0
54.63510555424817,52.21388588061123,0
33.91550010906887,98.86943574220611,0
64.17698887494485,80.90806058670817,1
74.78925295941542,41.57341522824434,0
34.1836400264419,75.2377203360134,0
83.90239366249155,56.30804621605327,1
51.54772026906181,46.85629026349976,0
94.44336776917852,65.56892160559052,1
82.36875375713919,40.61825515970618,0
51.04775177128865,45.82270145776001,0
62.22267576120188,52.06099194836679,0
77.19303492601364,70.45820000180959,1
97.77159928000232,86.7278223300282,1
62.07306379667647,96.76882412413983,1
91.56497449807442,88.69629254546599,1
79.94481794066932,74.16311935043758,1
99.2725269292572,60.99903099844988,1
90.54671411399852,43.39060180650027,1
34.52451385320009,60.39634245837173,0
50.2864961189907,49.80453881323059,0
49.58667721632031,59.80895099453265,0
97.64563396007767,68.86157272420604,1
32.57720016809309,95.59854761387875,0
74.24869136721598,69.82457122657193,1
71.79646205863379,78.45356224515052,1
75.3956114656803,85.75993667331619,1
35.28611281526193,47.02051394723416,0
56.25381749711624,39.26147251058019,0
30.05882244669796,49.59297386723685,0
44.66826172480893,66.45008614558913,0
66.56089447242954,41.09209807936973,0
40.45755098375164,97.53518548909936,1
49.07256321908844,51.88321182073966,0
80.27957401466998,92.11606081344084,1
66.74671856944039,60.99139402740988,1
32.72283304060323,43.30717306430063,0
64.0393204150601,78.03168802018232,1
72.34649422579923,96.22759296761404,1
60.45788573918959,73.09499809758037,1
58.84095621726802,75.85844831279042,1
99.82785779692128,72.36925193383885,1
47.26426910848174,88.47586499559782,1
50.45815980285988,75.80985952982456,1
60.45555629271532,42.50840943572217,0
82.22666157785568,42.71987853716458,0
88.9138964166533,69.80378889835472,1
94.83450672430196,45.69430680250754,1
67.31925746917527,66.58935317747915,1
57.23870631569862,59.51428198012956,1
80.36675600171273,90.96014789746954,1
68.46852178591112,85.59430710452014,1
42.0754545384731,78.84478600148043,0
75.47770200533905,90.42453899753964,1
78.63542434898018,96.64742716885644,1
52.34800398794107,60.76950525602592,0
94.09433112516793,77.15910509073893,1
90.44855097096364,87.50879176484702,1
55.48216114069585,35.57070347228866,0
74.49269241843041,84.84513684930135,1
89.84580670720979,45.35828361091658,1
83.48916274498238,48.38028579728175,1
42.2617008099817,87.10385094025457,1
99.31500880510394,68.77540947206617,1
55.34001756003703,64.9319380069486,1
74.77589300092767,89.52981289513276,1

二、问题再现：

        在这部分的练习中，你将建立一个逻辑回归模型来预测一个学生是否被大学录取。

        假设你是一所大学系的管理员，你想根据两次考试的成绩来决定每个申请人的录取机会。你有以前申请者的历史数据，可以用作逻辑回归的训练集。对于每个培训示例，您都有申请人在两次考试中的分数和录取决定。

        你的任务是依据这两门考试的成绩建立一个分类模型来估计每一位申请人的录取可能性。

三、Python实现思路：

• 引入所需的包

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.optimize as opt

• 设置路径并读取数据集

path = "D:\BaiduNetdiskDownload\ex2\ex2data1.txt"
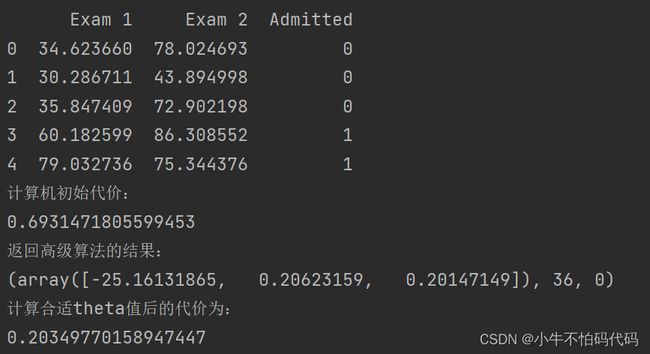
data = pd.read_csv(path, header=None, names=['Exam 1', 'Exam 2', 'Admitted'])
print(data.head())

        注：在这里数据集的地址是你个人在本地保存的地址。

• 找出结果分别为1和0的数据集并且赋值以名称

positive = data[data['Admitted'].isin([1])] #取Admitted这一行，用isin函数查看是否存在1，若存在返回布尔值true1
negative = data[data['Admitted'].isin([0])]

• 定义代价函数

        首先定义sigmoid函数，它的数学形式为：

        Python实现为：

def sigmoid(z):
    return 1/(1 + np.exp(-z))

        假设函数定义为：

        代价函数的推导过程为：

        要想取得最大似然估计，可令代价函数为：

        求导得：

        Python实现为：

def computeCost(theta, X, y):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    first = np.multiply(y, np.log(sigmoid(X * theta.T)))
    second = np.multiply((1-y), np.log(1-sigmoid(X * theta.T)))
    return -(np.sum(first + second) / (len(X)))

• 初始化数据

data.insert(0, 'Ones', 1)
cols = data.shape[1]
X = data.iloc[:, 0:cols-1]
y = data.iloc[:, cols-1:cols]
theta = np.zeros(3)
X = np.matrix(X.values)
y = np.matrix(y.values)
print("计算机初始代价：")
print(computeCost(theta, X, y))

• 使用高级优化算法，以求得最合适的θ的值

def gredientDecent(theta, X, y):
    X = np.matrix(X)
    y = np.matrix(y)
    theta = np.matrix(theta)
    parameters =int(theta.ravel().shape[1])#多维降一维
    grad = np.zeros(parameters)
    error = sigmoid(X * theta.T) - y
    for i in range(parameters):
        term = np.multiply(error, X[:, i])
        grad[i] = np.sum(term) / len(X)
    return grad

        利用Scipy高级优化算法求theta[0]：fmin_tnc()有约束的多元函数问题，提供梯度信息，使用截断牛顿法。

        参数的定义如下：

                func：优化的目标函数

                x0：初值

                fprime：提供优化函数func的梯度函数，不然优化函数func必须返回函数值和梯度，或者设置approx_grad=True

                approx_grad:如果设置为True，会给出近似梯度

                args：元组，是传递给优化函数的参数

result = opt.fmin_tnc (func = computeCost, x0 = theta, fprime = gredientDecent, args = (X, y))
print("返回高级算法的结果：")
print(result)
print("计算合适theta值后的代价为：")
print(computeCost(result[0], X, y))

• 绘图

plotting_x1 = np.linspace(30, 100, 100) #构造等差数列，在30到100分之间，分隔100份
plotting_h1 = (-(result[0][0] + result[0][1] * plotting_x1)) / result[0][2]
#根据h1公式计算，-（theta[0]+theta[1]*x）/theta[2]，此公式可以得到散点图的决策边界，是提前给的

fig,ax = plt.subplots(figsize = (8,6)) #8行6列
ax.plot(plotting_x1, plotting_h1, 'y', label = 'Prediction')
ax.scatter(positive['Exam 1'], positive['Exam 2'], s=50, c='b', marker='o', label='Admitted')
ax.scatter(negative['Exam 1'], negative['Exam 2'], s=50, c='r', marker='x', label='Not Admitted')
ax.legend()
ax.set_xlabel('Exam 1 Score')
ax.set_ylabel('Exam 2 Score')
plt.show()

• 根据求出的θ的值进行预测并计算准确率

def hfunc(theta, X):
    return sigmoid(X * theta.T)
pre = [1,45,85]
pre = np.matrix(pre)
the = np.matrix(result[0])
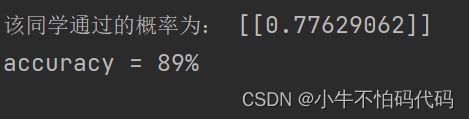
print("该同学通过的概率为：", hfunc(the, pre))

#计算准确率
def predict(theta, X):
    probability = sigmoid(X * theta.T) #theta为1*3，X为100*3,theta.T为3*1矩阵
    return [1 if x >= 0.5 else 0 for x in probability]   #如果x>0.5,则输出1，否则x位于probability则为0

theta_min = np.matrix(result[0])
predictions = predict(theta_min, X) #此函数theta_min为1*3的矩阵，X必须在之前设置为array或matrix，否则dataframe不可用，为100*3
correct = [1 if ((a == 1 and b == 1) or (a == 0 and b == 0)) else 0 for (a, b) in zip(predictions, y)]
accuracy = (sum(map(int, correct)) % len(correct))
print ('accuracy = {0}%'.format(accuracy))

四、完整代码如下：

1. import numpy as np
   import pandas as pd
   import matplotlib.pyplot as plt
   import scipy.optimize as opt
   
   # 读取数据集
   path = "D:\BaiduNetdiskDownload\ex2\ex2data1.txt"
   data = pd.read_csv(path, header=None, names=['Exam 1', 'Exam 2', 'Admitted'])
   print(data.head())
   
   #找出结果分别为1和0的数据集并且赋值以名称，
   positive = data[data['Admitted'].isin([1])] #取Admitted这一行，用isin函数查看是否存在1，若存在返回布尔值true1
   negative = data[data['Admitted'].isin([0])]
   
   #定义代价函数
   def sigmoid(z):
       return 1/(1 + np.exp(-z))
   
   def computeCost(theta, X, y):
       theta = np.matrix(theta)
       X = np.matrix(X)
       y = np.matrix(y)
       first = np.multiply(y, np.log(sigmoid(X * theta.T)))
       second = np.multiply((1-y), np.log(1-sigmoid(X * theta.T)))
       return -(np.sum(first + second) / (len(X)))
   
   #初始化数据
   data.insert(0, 'Ones', 1)
   cols = data.shape[1]
   X = data.iloc[:, 0:cols-1]
   y = data.iloc[:, cols-1:cols]
   theta = np.zeros(3)
   X = np.matrix(X.values)
   y = np.matrix(y.values)
   print("计算机初始代价：")
   print(computeCost(theta, X, y))
   
   #高级优化算法 共轭梯度法求theta,先对梯度进行计算（此处使用函数名为gredientDecent，其实这个函数并没有下降theta的作用），循环次数为theta值的个数，计算出的就是每个theta值对应的梯度（代价函数的导数），计算后返回计算出的梯度向量。
   def gredientDecent(theta, X, y):
       X = np.matrix(X)
       y = np.matrix(y)
       theta = np.matrix(theta)
       parameters =int(theta.ravel().shape[1])#多维降一维
       grad = np.zeros(parameters)
       error = sigmoid(X * theta.T) - y
       for i in range(parameters):
           term = np.multiply(error, X[:, i])
           grad[i] = np.sum(term) / len(X)
       return grad
   #Scipy高级优化算法求theta[0]：fmin_tnc()有约束的多元函数问题，提供梯度信息，使用截断牛顿法。
       '''func：优化的目标函数
   
       x0：初值
   
       fprime：提供优化函数func的梯度函数，不然优化函数func必须返回函数值和梯度，或者设置approx_grad=True
   
       approx_grad :如果设置为True，会给出近似梯度
   
       args：元组，是传递给优化函数的参数'''
   result = opt.fmin_tnc (func = computeCost, x0 = theta, fprime = gredientDecent, args = (X, y))
   print("返回高级算法的结果：")
   print(result)
   print("计算合适theta值后的代价为：")
   print(computeCost(result[0], X, y))
   
   #绘制散点图，并且绘制决策线
   plotting_x1 = np.linspace(30, 100, 100) #构造等差数列，在30到100分之间，分隔100份
   plotting_h1 = (-(result[0][0] + result[0][1] * plotting_x1)) / result[0][2]
   #根据h1公式计算，-（theta[0]+theta[1]*x）/theta[2]，此公式可以得到散点图的决策边界，是提前给的
   
   fig,ax = plt.subplots(figsize = (8,6)) #8行6列
   ax.plot(plotting_x1, plotting_h1, 'y', label = 'Prediction')
   ax.scatter(positive['Exam 1'], positive['Exam 2'], s=50, c='b', marker='o', label='Admitted')
   ax.scatter(negative['Exam 1'], negative['Exam 2'], s=50, c='r', marker='x', label='Not Admitted')
   ax.legend()
   ax.set_xlabel('Exam 1 Score')
   ax.set_ylabel('Exam 2 Score')
   plt.show()
   
   #预测通过的概率
   def hfunc(theta, X):
       return sigmoid(X * theta.T)
   pre = [1,45,85]
   pre = np.matrix(pre)
   the = np.matrix(result[0])
   print("该同学通过的概率为：", hfunc(the, pre))
   
   #计算准确率
   def predict(theta, X):
       probability = sigmoid(X * theta.T) #theta为1*3，X为100*3,theta.T为3*1矩阵
       return [1 if x >= 0.5 else 0 for x in probability]   #如果x>0.5,则输出1，否则x位于probability则为0
   
   theta_min = np.matrix(result[0])
   predictions = predict(theta_min, X) #此函数theta_min为1*3的矩阵，X必须在之前设置为array或matrix，否则dataframe不可用，为100*3
   correct = [1 if ((a == 1 and b == 1) or (a == 0 and b == 0)) else 0 for (a, b) in zip(predictions, y)]
   accuracy = (sum(map(int, correct)) % len(correct))
   print ('accuracy = {0}%'.format(accuracy))

五、最后结果：

        本文是我个人的学习记录，由于本人才疏学浅，在学习的过程中是边参考着别人的知识总结边学习的，以下是我参考的链接：

(1条消息) 吴恩达机器学习中文版课后题（中文题目+数据集+python版答案）week2 逻辑回归_cv吴彦祖的博客-CSDN博客_吴恩达机器学习作业数据集https://blog.csdn.net/wangjia2575525474/article/details/119977534

(1条消息) 吴恩达机器学习课后作业深度解析（附答案）（ex2）_布衣书生real的博客-CSDN博客_吴恩达机器学习作业https://blog.csdn.net/m0_37830950/article/details/84845257

        若大家发现本文有任何不当或不正确之处，请在评论区批评指正，我会及时查看并加以修正！