吴恩达机器学习课后习题ex2(续)
ex2: Regularized logistic regression
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn import linear_model
import scipy.optimize as opt
from sklearn.metrics import classification_report
def raw_data(path):
data = pd.read_csv(path,names=['test1','test2','accept'])
return data
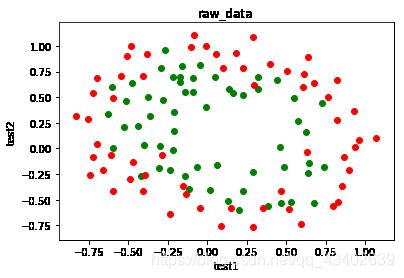
def draw_data(data):
accept = data[data.accept == 1]#合格
reject = data[data.accept == 0]#不合格
plt.scatter(accept.test1,accept.test2,c='g',label = 'qualified')
plt.scatter(reject.test1,reject.test2,c='r',label = 'not qualified')
plt.title('raw_data')
plt.xlabel('test1')
plt.ylabel('test2')
return plt
特征映射参考资料:
https://www.zhihu.com/question/65020904
def feature_mapping(x1,x2,power):
datamap = {}
for i in range(power+1):
for j in range(i+1):
datamap['f{}{}'.format(j,i-j)] = np.power(x1,j)*np.power(x2,i-j)
#产生x1,x2的多项式
return pd.DataFrame(datamap)
def sigmoid(z):
return 1/(1+np.exp(-z))
numpy与pandas数据格式详细介绍(含pd.DataFrame)
https://zhuanlan.zhihu.com/p/35592464
#正则化代价函数
def regularized_cost_function(theta,x,y,lam):
m = x.shape[0]#总例数
j = (y.dot(np.log(sigmoid(x.dot(theta))))+(1-y).dot(np.log(1-sigmoid(x.dot(theta)))))/(-m)
#加上惩罚项
penalty = lam*(theta.dot(theta))/(2*m)
return j+penalty
#计算偏导数
def regularized_gradient_descent(theta,x,y,lam):
m = x.shape[0]
partial_j = ((sigmoid(x.dot(theta))-y).T).dot(x)/m
partial_penalty = lam*theta/m
partial_penalty[0] = 0 #第一项不惩罚
return partial_j+partial_penalty
def predict(theta,x):
h = x.dot(theta)
return [1 if x >= 0.5 else 0 for x in h]
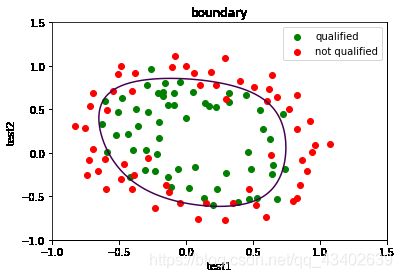
#确定边界线
def boundary(theta,data,x,y):
[X,Y] = np.meshgrid(x,y)
x = np.linspace(-1,1.5,200)
x1, x2 = np.meshgrid(x,x) #???
z = feature_mapping(x1.ravel(),x2.ravel(),6).values
z = z.dot(theta)
z = z.reshape(x1.shape)
plt = draw_data(data)
plt.contour(x1,x2,z,0)
plt.title('boundary')
plt.legend(loc=0)
plt.show()
numpy.meshgrid()理解
https://blog.csdn.net/lllxxq141592654/article/details/81532855
https://mp.weixin.qq.com/s?src=11×tamp=1562830720&ver=1721&signature=G*zsqj91mOIJlkmVRbOPLVtwWhRlWC5nDNkl6ER*OVIwJouILIY-3lbOQVRJ4sBXMpIKadps89EEvvhHCdMeU1PcbtLiQ1ATe*emOK3She2najTzQ04m97vjf6Lo4ak3&new=1
numpy 中的reshape,flatten,ravel 数据平展,多维数组变成一维数组
https://www.cnblogs.com/onemorepoint/p/9551762.html
def main():
rawdata = raw_data('ex2data2.txt')
plt = draw_data(rawdata)
plt.show()
data = feature_mapping(rawdata['test1'],rawdata['test2'],power=6)
#函数数据进行特征映射处理
print(data.head())#处理后的数据
x = data.values
y = rawdata['accept']
theta = np.zeros(x.shape[1])#初始化参数theta
theta=opt.minimize(fun=regularized_cost_function,x0=theta,args=(x,y,1),method='tnc',jac=regularized_gradient_descent)
theta=theta.x
boundary(theta,rawdata,x,y)
main()
f00 f01 f10 f02 f11 f20 f03 f12 \
0 1.0 0.69956 0.051267 0.489384 0.035864 0.002628 0.342354 0.025089
1 1.0 0.68494 -0.092742 0.469143 -0.063523 0.008601 0.321335 -0.043509
2 1.0 0.69225 -0.213710 0.479210 -0.147941 0.045672 0.331733 -0.102412
3 1.0 0.50219 -0.375000 0.252195 -0.188321 0.140625 0.126650 -0.094573
4 1.0 0.46564 -0.513250 0.216821 -0.238990 0.263426 0.100960 -0.111283
f21 f30 ... f32 f41 f50 \
0 0.001839 0.000135 ... 0.000066 0.000005 3.541519e-07
1 0.005891 -0.000798 ... -0.000374 0.000051 -6.860919e-06
2 0.031616 -0.009761 ... -0.004677 0.001444 -4.457837e-04
3 0.070620 -0.052734 ... -0.013299 0.009931 -7.415771e-03
4 0.122661 -0.135203 ... -0.029315 0.032312 -3.561597e-02
f06 f15 f24 f33 f42 f51 \
0 0.117206 0.008589 0.000629 0.000046 0.000003 2.477505e-07
1 0.103256 -0.013981 0.001893 -0.000256 0.000035 -4.699318e-06
2 0.110047 -0.033973 0.010488 -0.003238 0.001000 -3.085938e-04
3 0.016040 -0.011978 0.008944 -0.006679 0.004987 -3.724126e-03
4 0.010193 -0.011235 0.012384 -0.013650 0.015046 -1.658422e-02
f60
0 1.815630e-08
1 6.362953e-07
2 9.526844e-05
3 2.780914e-03
4 1.827990e-02
[5 rows x 28 columns]
参考学习博客:
https://blog.csdn.net/zy1337602899/article/details/84777396
https://blog.csdn.net/Cowry5/article/details/80247569