吴恩达机器学习课程ex2 Python实现

逻辑回归

在训练的初始阶段，我们将要构建一个逻辑回归模型来预测，某个学生是否被大学录取。
设想你是大学相关部分的管理者，想通过申请学生两次测试的评分，来决定他们是否被录取。
现在你拥有之前申请学生的可以用于训练逻辑回归的训练样本集。对于每一个训练样本，你有他们两次测试的评分和最后是被录取的结果

数据可视化

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

#读取数据
path = 'ex2data1.txt'
data = pd.read_csv(path,header = None, names=['Exam1','Exam2','Admitted'])
data.head()

	Exam1	Exam2	Admitted
0	34.623660	78.024693	0
1	30.286711	43.894998	0
2	35.847409	72.902198	0
3	60.182599	86.308552	1
4	79.032736	75.344376	1

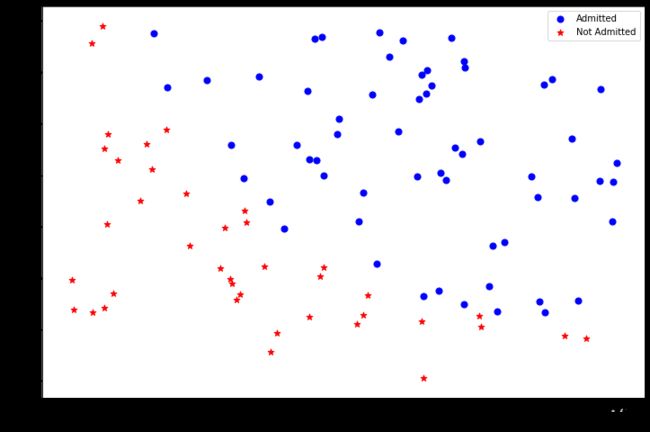
#可视化
positive = data[data['Admitted']==1]
negative = data[data['Admitted']==0]
fig,ax = plt.subplots(figsize=(12,8))
ax.scatter(positive['Exam1'],positive['Exam2'],s=50,c='b',marker = 'o',label='Admitted')
ax.scatter(negative['Exam1'],negative['Exam2'],s=50,c='r',marker = '*',label='Not Admitted')
ax.legend()
ax.set_xlabel('Exam1 Score')
ax.set_ylabel('Exam2 Score')
plt.show()

逻辑回归实现

sigmoid函数

def sigmoid(z):
    return 1/(1+np.exp(-z))

代价函数和梯度

def cost(theta,X,y):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    left = np.multiply(-y,np.log(sigmoid(X*theta.T)))
    right = np.multiply((1-y),np.log(1-sigmoid(X*theta.T)))
    return np.sum(left-right)/(len(X))

# 初始化X,y,theta
data.insert(0,'Ones',1)

cols = data.shape[1]
X = data.iloc[:,:cols-1]
y = data.iloc[:,cols-1:cols]
theta = np.zeros(3)
X = np.array(X.values)
y = np.array(y.values)

#确认三个矩阵的维度
X.shape,y.shape,theta.shape

((100, 3), (100, 1), (3,))

cost(theta,X,y)

0.6931471805599453

#实现梯度计算但是不更新theta
def gradient(theta,X,y):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    
    parameters = int(theta.ravel().shape[1])
    grad = np.zeros(parameters)
    
    error = sigmoid(X*theta.T) - y
    
    for i in range(parameters):
        grad[i] = np.sum(np.multiply(X[:,i],error))/len(X)
    
    return grad

用工具库计算 $\theta$

在此前的线性回归中，我们自己写代码实现的梯度下降（ex1的2.2.4的部分）。当时我们写了一个代价函数、计算了他的梯度，然后对他执行了梯度下降的步骤。这次，我们不自己写代码实现梯度下降，我们会调用一个已有的库。这就是说，我们不用自己定义迭代次数和步长，功能会直接告诉我们最优解。
andrew ng在课程中用的是Octave的“fminunc”函数，由于我们使用Python，我们可以用scipy.optimize.fmin_tnc做同样的事情。

import scipy.optimize as opt
result = opt.fmin_tnc(func=cost,x0=theta,fprime = gradient,args=(X,y))
result

(array([-25.16131863,   0.20623159,   0.20147149]), 36, 0)

p.s.

fmin_tnc()
有约束的多元函数问题，提供梯度信息，使用截断牛顿法。

调用：

scipy.optimize.fmin_tnc(func, x0, fprime=None, args=(), approx_grad=0, bounds=None, epsilon=1e-08, scale=None, offset=None, messages=15, maxCGit=-1, maxfun=None, eta=-1, stepmx=0, accuracy=0, fmin=0, ftol=-1, xtol=-1, pgtol=-1, rescale=-1, disp=None, callback=None)

最常使用的参数：

func：优化的目标函数

x0：初值

fprime：提供优化函数func的梯度函数，不然优化函数func必须返回函数值和梯度，或者设置approx_grad=True

approx_grad :如果设置为True，会给出近似梯度

args：元组，是传递给优化函数的参数

返回：

x ： 数组，返回的优化问题目标值

nfeval ： 整数，function evaluations的数目

在进行优化的时候，每当目标优化函数被调用一次，就算一个function evaluation。在一次迭代过程中会有多次function evaluation。这个参数不等同于迭代次数，而往往大于迭代次数。

rc ： int,Return code, see below

#用算法得出的theta值计算cost值
cost(result[0],X,y)

0.20349770158947458

plotting_x1 = np.linspace(30,100,100)
plotting_exam2_predicted = (-result[0][0]-result[0][1]*plotting_x1)/result[0][2]

fig,ax = plt.subplots(figsize=(12,8))
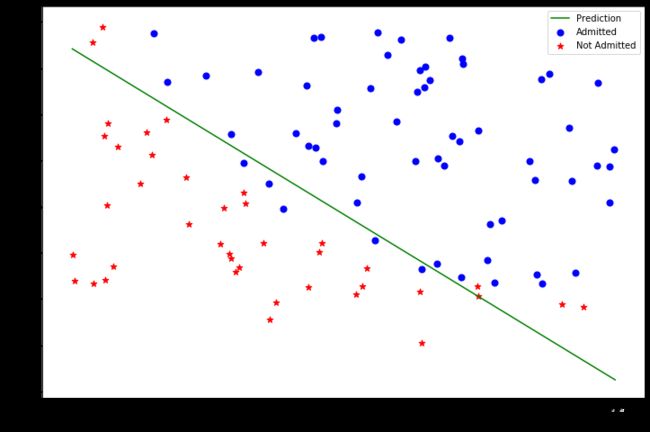
ax.plot(plotting_x1,plotting_exam2_predicted,'g',label='Prediction')
ax.scatter(positive['Exam1'],positive['Exam2'],s=50,c='b',marker = 'o',label='Admitted')
ax.scatter(negative['Exam1'],negative['Exam2'],s=50,c='r',marker = '*',label='Not Admitted')
ax.legend()
ax.set_xlabel('Exam1 Score')
ax.set_ylabel('Exam2 Score')
plt.show()

评价逻辑回归模型

在确定参数之后，我们可以使用这个模型来预测学生是否录取。如果一个学生exam1得分45，exam2得分85，那么他录取的概率应为0.776。另一种评价θ的方法是看模型在训练集上的正确率怎样。写一个predict的函数，给出数据以及参数后，会返回“1”或者“0”。然后再把这个predict函数用于训练集上，看准确率怎样。

#实现htheta
def hfunc1(theta, X):
    return sigmoid(np.dot(theta.T, X))
hfunc1(result[0],[1,45,85])

0.7762906238162848

#定义predict函数
def predict(theta,X):
    probability = sigmoid(X*theta.T)
    return[1 if x > 0.5 else 0 for x in probability]

#统计正确率
theta_min = np.matrix(result[0])
predictions = predict(theta_min,X)

correct = [1 if (a==1 and b==1) or (a==0 and b==0) else 0 for (a,b)in zip(predictions,y)]
accuracy = (sum(correct))%len(correct)
print ('accuracy = {0}%'.format(accuracy))

accuracy = 89%

正则化逻辑回归

在训练的第二部分，我们将实现加入正则项提升逻辑回归算法。
设想你是工厂的生产主管，你有一些芯片在两次测试中的测试结果，测试结果决定是否芯片要被接受或抛弃。你有一些历史数据，帮助你构建一个逻辑回归模型。

数据可视化

path = 'ex2data2.txt'
data_init = pd.read_csv(path,header = None,names=['Test1','Test2','Accepted'])
data_init.head()

	Test1	Test2	Accepted
0	0.051267	0.69956	1
1	-0.092742	0.68494	1
2	-0.213710	0.69225	1
3	-0.375000	0.50219	1
4	-0.513250	0.46564	1

positive2 = data_init[data_init.Accepted==1]
negative2 = data_init[data_init.Accepted==0]

fig,ax = plt.subplots(figsize=(12,8))
ax.scatter(positive2.Test1,positive2.Test2,c='b',marker = 'o',label='Test1')
ax.scatter(negative2.Test1,negative2.Test2,c='r',marker = 'x',label='Test2')
ax.legend()
ax.set_xlabel('Test1')
ax.set_ylabel('Test2')
plt.show()

不适用于线性切割，所以不能直接使用逻辑回归

特征映射

一种更好的使用数据集的方式是为每组数据创造更多的特征。所以我们为每组添加了最高到6次幂的特征

degree = 6
data2 = data_init
#x1 = data2['Test1']
#x2 = data2['Test2']
#data2.insert(3,'Ones',1)

for i in range(1,degree+1):
    for j in range(0,i+1):
        data2['F'+str(i-j)+str(j)] = np.power(x1,i-j)*np.power(x2,j)
        
#data2.drop('Test1',axis=1,inplace = True)
#data2.drop('Test2',axis=1,inplace = True)
data2.shape

(118, 29)

代价函数和梯度

在普通的梯度计算中加入惩罚项

#实现正则化的代价函数
def costReg(theta,X,y,learningRate):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    
    left = np.multiply(-y,np.log(sigmoid(X*theta.T)))
    right = np.multiply(1-y,np.log(1-sigmoid(X*theta.T)))
    reg = (learningRate/(2*len(X)))*np.sum(np.power(theta[:,1:theta.shape[1]],2))
    return np.sum(left-right)/len(X) + reg

#实现正则化的梯度函数
def gradientReg(theta,X,y,learningRate):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    
    parameters = int(theta.ravel().shape[1])
    grad = np.zeros(parameters)
    
    error = sigmoid(X*theta.T) - y
    
    for i in range(parameters):
        term = np.multiply(error,X[:,i])
        
        if(i==0):
            grad[i] = np.sum(term)/len(X)
        else:
            grad[i] = (np.sum(term)/len(X) + (learningRate/len(X))*theta[:,i])

            
    return grad
    

#初始化X,y,theta
cols = data2.shape[1]
X2 = data2.iloc[:,1:cols]
y2 = data2.iloc[:,0:1]
theta2 = np.zeros(cols-1)

#类型转换
X2 = np.matrix(X2.values)
y2 = np.matrix(y2.values)

learningRate = 1

#计算初始代价
costReg(theta2,X2,y2,learningRate)

0.6931471805599454

#用工具库求解参数
result2 = opt.fmin_tnc(func = costReg,x0 = theta2,fprime = gradientReg,args=(X2,y2,learningRate))
result2

(array([ 1.27271026,  0.62529965,  1.18111686, -2.01987399, -0.91743189,
        -1.43166929,  0.12393227, -0.36553118, -0.35725404, -0.17516291,
        -1.45817009, -0.05098418, -0.61558554, -0.27469165, -1.19271298,
        -0.2421784 , -0.20603299, -0.04466178, -0.2777895 , -0.29539513,
        -0.45645982, -1.04319155,  0.02779373, -0.2924487 ,  0.0155576 ,
        -0.32742405, -0.1438915 , -0.92467487]), 32, 1)

theta_min = np.matrix(result2[0])
predictions = predict(theta_min,X2)
correct = [1 if ((a == 1 and b == 1) or (a == 0 and b == 0)) else 0 for (a, b) in zip(predictions, y2)]
accuracy = (sum(map(int, correct)) / len(correct))*100
print ('accuracy = {0}%'.format(accuracy))

accuracy = 83.05084745762711%

画出决策曲线

degree = 6
def hfunc2(theta,x1,x2):
    temp = theta[0][0]
    place = 0
    
    for i in range(1,degree+1):
        for j in range(0,i+1):
            temp += np.power(x1,i-j)*np.power(x2,j)*theta[0][place+1]
            place +=1
    return temp

def find_decision_boundary(theta):
    t1 = np.linspace(-1,1.5,1000)
    t2 = np.linspace(-1,1.5,1000)
    cordinates = [(x,y) for x in t1 for y in t2]
    x_cord,y_cord = zip(*cordinates)
    h_val = pd.DataFrame({'x1':x_cord,'x2':y_cord})
    h_val['hval'] = hfunc2(theta,h_val['x1'],h_val['x2'])
    
    decision = h_val[np.abs(h_val['hval'])<2*10**-3]
    return decision.x1,decision.x2
    

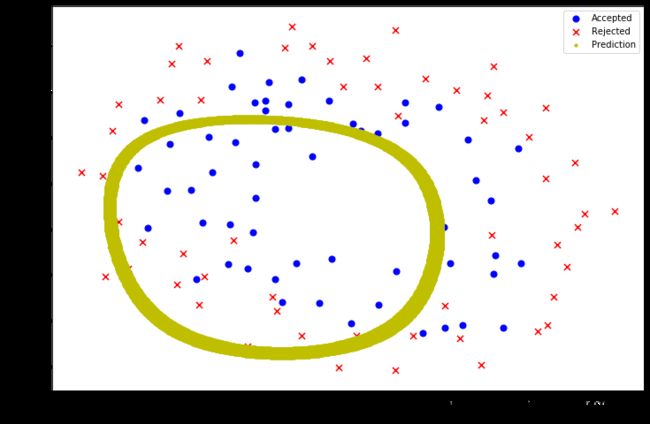
fig, ax = plt.subplots(figsize=(12,8))
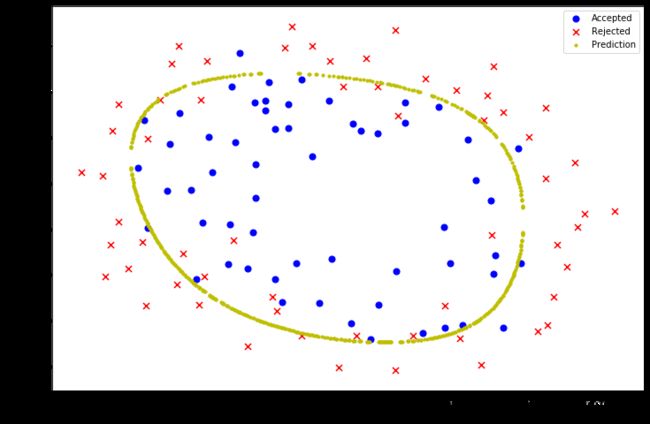
ax.scatter(positive2['Test1'], positive2['Test2'], s=50, c='b', marker='o', label='Accepted')
ax.scatter(negative2['Test1'], negative2['Test2'], s=50, c='r', marker='x', label='Rejected')
ax.set_xlabel('Test 1 Score')
ax.set_ylabel('Test 2 Score')

x, y = find_decision_boundary(result2)
plt.scatter(x, y, c='y', s=10, label='Prediction')
ax.legend()
plt.show()

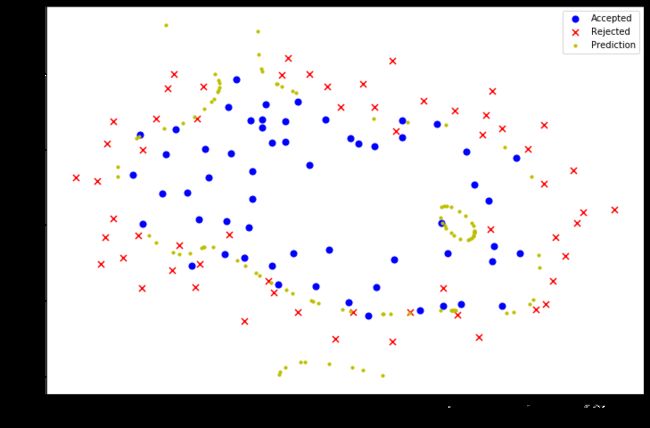
#当lambda=0时过拟合
learningRate2 = 0
result3 = opt.fmin_tnc(func=costReg,x0=theta2,fprime=gradientReg,args=(X2,y2,learningRate2))

fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(positive2['Test1'], positive2['Test2'], s=50, c='b', marker='o', label='Accepted')
ax.scatter(negative2['Test1'], negative2['Test2'], s=50, c='r', marker='x', label='Rejected')
ax.set_xlabel('Test 1 Score')
ax.set_ylabel('Test 2 Score')

x, y = find_decision_boundary(result3)
plt.scatter(x, y, c='y', s=10, label='Prediction')
ax.legend()
plt.show()

#当lambda=1000时欠拟合
learningRate3 = 100
result4 = opt.fmin_tnc(func=costReg, x0=theta2, fprime=gradientReg, args=(X2, y2, learningRate3))

fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(positive2['Test1'], positive2['Test2'], s=50, c='b', marker='o', label='Accepted')
ax.scatter(negative2['Test1'], negative2['Test2'], s=50, c='r', marker='x', label='Rejected')
ax.set_xlabel('Test 1 Score')
ax.set_ylabel('Test 2 Score')

x, y = find_decision_boundary(result4)
plt.scatter(x, y, c='y', s=10, label='Prediction')
ax.legend()
plt.show()