integral函数Opencv源码理解-leetcode动态规划的使用场景

前言

            Opencv有一个integral()函数，也就是积分图算法。有三种积分图类型，求和（sum），求平方和(sqsum)，求旋转45°和(titled)。根据名字可知道，前两个是统计输出每个坐标的左上方像素和、左上方像素平方和，旋转45°的积分图则是统计每个像素点左上方45°到右上方45°区域的像素和。

        作为一名合格的算法工程师，肯定都有leetcode的刷题经验，leetcode上的经典动态规划类型题目，可以完美的在integral函数的代码中体现。

        通过本文，你会知道积分图的sum, sqsum, titled的使用和实现细节。看到动态规划中时间复杂度和内存优化的思想是如何被一步步设计的。

integral()函数的介绍

        积分图是数字图像处理中常用的一种方法，通常能够很大程度的加速计算过程。其思想是，当需要统计一张图像中矩形区域的像素和时候，如果我们之前统计过该图像的积分图结果，就可以直接调用积分图数据，做两次加法两次减法就能得到结果了，而不用再遍历这个图像的所有像素点。

        如下图，假设积分图用summ表示, ABCD区域的像素和用S表示，则S=summ[A] + summ[D]-summ[C]-summ[B]。粉色标记区域就是点A的累计像素和区域，分别对应了sum, sqsum积分图和titled积分图。

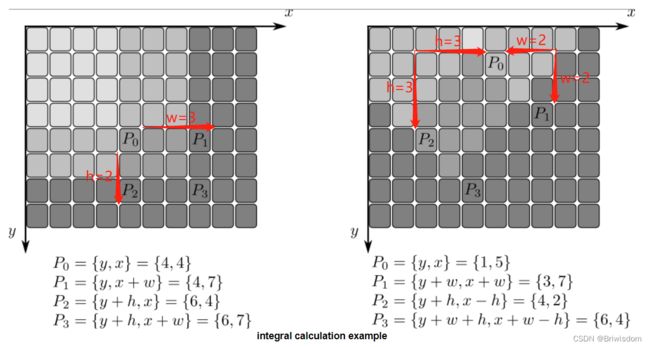
        另外，使用积分图时候，一般会给一个左上角的点A(x,y, h,w), 其对应的矩形B，C，D的坐标关系，在sum，titled里具有不一样的含义。比如在opencv 文档里的示例，一个正常的矩形 Rect(4,4,3,2) 和一个倾斜45度的矩形Rect(5,1,2,3)。其坐标对应关系如下，请注意stright和titled矩形的P0,P1,P2,P3并非一一对应，只有同一张图里的P0,P1,P2,P3四个点的相对位置是对应的，这里可能会给人造成误解。

        integral积分图有三种构建方式，定义如下。前两种sum，sqsum比如可以用在相似度匹配算法NCC， 第三种titled常用在人脸检测算法的Harr特征提取场景。

 integral的代码实现设计

        由定义可知，sum, sqsum两种积分图除了累加定义不同，其实现思路是一样的。为了描述方便，后面代码设计主要以sum，title两种方式为典型进行分析。

sum模式的代码实现设计

        把一张图按照从左到右，从上到下的顺序遍历，sum是以统计每个像素点的之前的像素值累计之和，那么如果没有优化思想，每个输出像素点都要重新从头开始遍历图像并累加和，那么时间复杂度就是O(H *W *(1+2+3+...+H*W)≈O（H*W）^2，实际上完全没有必要。

        根据定义，我们可以发现当前像素点的积分结果与其左边和上边一个是有关系的！利用这个关系，可以重复利用之前统计过的像素值，而不用重新统计新坐标位置之前的像素和了，实现“看一遍”就出结果的效果。

        如下图，假设原图用src表示, sum表示积分图结果。现在要计算p(x,y)的积分结果，可以有两种实现设计，其时间复杂度都是O(H*W), 只是空间复杂度不同。

设计一（左边）：

需要一个额外的空间数组Buf，长度和图像宽w相同。 buf[i]表示该列累计到i的像素和。

sum(x,y)=sum(x-1，y) +Buf(x-1)+src(x,y)

设计二（右边）：

需要一个额外空间变量Sx，表示该行累计到x坐标之前的像素和。

sum(x,y)=sum(x,y-1)+Sx+src(x,y)

titled模式的代码实现设计

        同样，我们也可以观察到titled模式的积分统计也是有规律的，当前像素的结果与其周边的几个点也有关系。最终也有两种实现设计方式。

        我们同样用src指代原图，用titled指代旋转45度的积分图结果。

设计一（左边）：

需要一个额外的空间数组Buf，长度和图像宽w相同。 buf[i]表示到第i行，其右斜对角的像素和。

titled(x,y)= titled(x-1,y-1)+Buf(x)+Buf(x+1)+src(x,y)

设计二（右边）：

titled(x,y)= titled(x-1,y-1)+ titled(x+1,y-1)- titled(x,y-2)+src(x,y)+src(x,y-1)

        另外对于titled模式，请注意，上面示意的只是中间位置像素点的计算，当第一行，或者第一列，最后一列时候的处理关系如下，上面两种设计对这种边界的处理是相同的。

• titled(x,y)=src(x,y),   if y=0
• titled(x,y)=titled(x+1,y-1)+src(x,y)+src(x,y-1),  if x=0
• titled(x,y)=titled(x-1,y-1)+src(x,y)+src(x,y-1),  if x=w-1

小结

        对于sum, titled，opencv的实现分别采用了设计2，设计1。并且为了使计算代码更简洁，在实现时候，sum,titled的内存分配都会比src多一行和一列。最终的结果在去掉这一行一列。

        至此，将integral积分图的代码实现流程已经分析完毕，sum, sqsum的计算比较容易复现，titled模式下，对维护每行斜对角累计像素和的Buf更新，有点不太容易理解。后面如果大家有需求，欢迎留言，再把我写的python实现代码贴一下，今天就到这里啦。

        整体代码实现的设计思路就是用到了动态规划的思想，想想自己之前刷过的题，感觉好亲切啊，有没有？