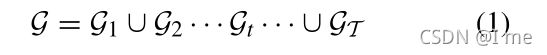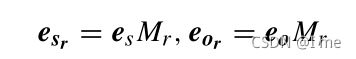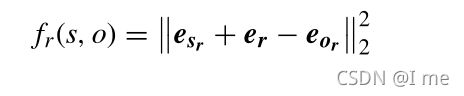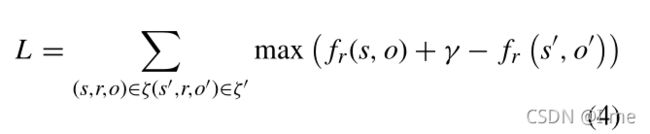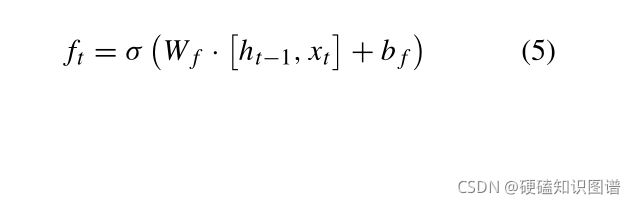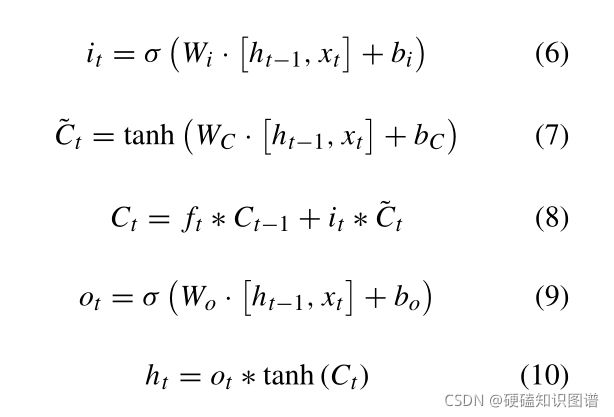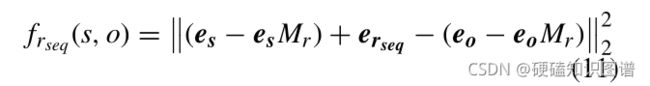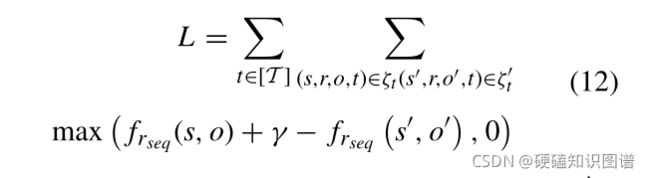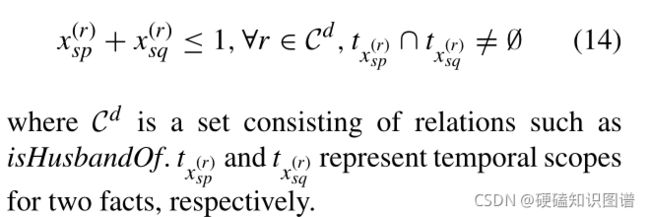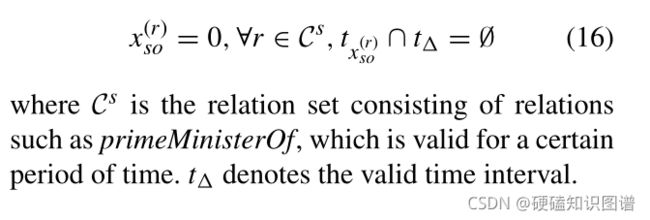具有时态一致性约束的时态知识图推理

论文：Reasoning over temporal knowledge graph with temporal consistency constraints

2.1.Static KGR

     TransE在处理复杂关系方面存在缺陷，例如一对多、多对一和多对多关系。为了解决这个问题，已经推导出了基于TransE的不同变体。

     TransH提出，实体在涉及不同关系时应具有不同的表示。它将头部和尾部实体投影到一个特定关系的超平面上。但是，TransH仍然表示同一空间中的实体和关系，这使得TransH无法精确地建模实体和关系。

    TransR，一个实体可能有多个方面，这取决于特定的关系，并将实体和关系投影到不同的向量空间中，事实上，尽管与TransE和TransH相比，TransR有显著的改进，但它也有一些缺陷。

     首先，头部和尾部实体共享相同的映射矩阵，这忽略了不同的实体属性。第二，由于矩阵向量乘法，transR比TransE和TransH更复杂。

    TransD  通过为每个实体关系对定义两个向量来构造动态映射矩阵，并用向量运算替换矩阵向量乘法，以降低模型复杂性。

2.2. Dynamic graph reasoning

   动态图推理旨在学习连续时间感知的节点表示，近年来受到了广泛的关注。

Nguyen等人提出了一个将时间信息纳入网络嵌入模型的框架，为从连续时间动态网络学习时间相关嵌入提供了基础。

DyRep提出了一种新的动态图建模框架，该框架将表示学习视为一个潜在的中介过程，其中两个被观察的过程，网络动态（实现为拓扑演化）和网络动态（实现为节点交互）桥接在一起。它将时间演化的结构信息编码为节点表示，考虑了时间注意机制.

DySAT通过对结构邻域和时间顺序表示的联合自我监督来计算动态节点表示，从而有效地捕获图形结构的时间演化模式。

Chen等人[3]提出了用于端到端链路预测的GC-LSTM，其中GCN是对每个时间滑动的网络节点结构学习的响应，而LSTM用于学习时间特征。

2.3. Temporal KGR

一些研究已经将静态KGR模型扩展到TKG。与动态图推理不同，时态KGR的目标是从时间戳事实中学习，并建立时间感知的推理表示。

t-TransE[11]利用时间敏感关系的时序来预测实体或关系；

TTransE[12]通过选择重要示例并将辅助信息纳入学习过程，专注于时间范围；

HyTE[5]通过将每个时间戳与相应的超平面关联，将时间合并到实体关系空间中。与以前的时间敏感嵌入方法相比，HyTE可以直接在学习的嵌入中编码时间信息。

Hybrid TE[26]结合TransD和HyTE对时间和多关系事实进行建模。为了获得令人满意的性能，Hybrid TE将每个事实映射到所有特定于时间的超平面，其中它是临时的而不是单一的超平面。

TA -TransE[8]是最类似于研究的工作，它将时间戳看作一个数字序列，并使用LSTM对关系向量和时间数字进行编码。然而，它无法捕获时间维度的交互，例如。时间一致性。

3. Preliminaries and background

3.1. Problem formulation

对于TKG，我们使用四元组 (s, r, o,[ts,te]),向三元组添加时间维度，以表示时间事实。对于四元组（s，r，o，[ts，te]），[ts，te]表示三元组（s，r，o）有效时的时间间隔，ts，te分别是事实的开始时间和结束时间，给定时间戳，TKG可以分解为一系列静态KG，这些KG由在单独的时间范围内有效的事实组成。TKG可以表示为：

 示例：四元组(Jean-Claude Juncker, is President Of,European Commission, [2014,2019]) 表明Jean-Claude Juncker是2014-2019年间的欧盟委员会主席。

时态知识图推理

TKGR的任务旨在根据TKG中的现有要素预测缺失事实，可分为三类：

主体实体预测：当关系、对象实体和时间给定时，预测主体实体，即。E？，r，o，t）。

对象实体预测：当对象实体、关系和时间给定时，预测对象实体。E（s，r，？，t）。

关系预测：当主体实体、客体实体和时间给定时，预测关系，即。E（s，？，o，t）。

3.2. TransR model

直观地说，相似的实体应该在实体空间中彼此靠近。然而，实体是多个属性的组合，不同的关系应该关注实体的不同属性。因此，在某些特定的方面，它们应该在相应的关系空间中彼此远离。为此，提出了TransR模型。对于每个三元组（s、r、o），它为每个关系假设一个语义空间，并通过投影矩阵M将实体映射到该语义空间，

 分数函数定义为：

TransR使用以下基于边缘的目标函数进行训练：

 

 其中，γ是边缘的超参数，ζ表示正三元组，ζ是通过随机替换主体或客体获得的负三元组。

4.时态感知推理模型

传统的推理方法通常定义评分函数fr(s, o)，常见的评分函数如下

 这些模型没有考虑到时间信息，这可能在处理复杂关系方面存在缺陷。为了解决这个问题，我们利用事实中包含的时间信息。

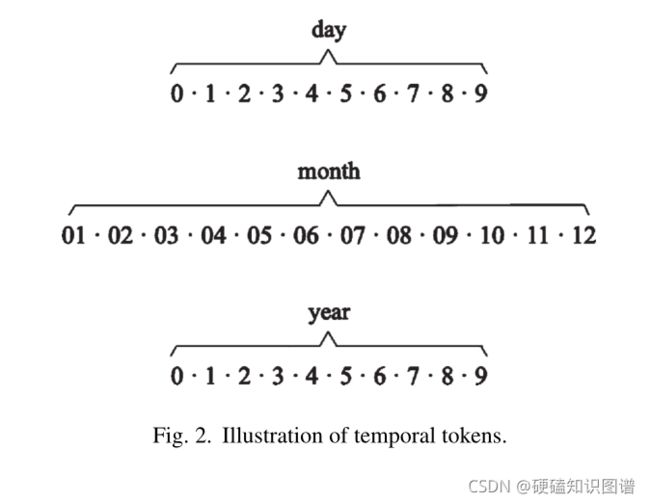
采用与TA TransE相同的操作[8]，我们首先将时间戳转换为带有时间令牌的序列，如图所示。

 长短时记忆网络LSTM

我们将关系、时间修饰符（如“ocursince”或“ocuruntil”）和时间数字放在一个序列中，表示为rseq；d,m, andy分别表示当前日期、月份和年份，我们将这些序列作为LSTM的输入

 4.1. LSTM for encoding time sequences

LSTM是一种特殊的递归神经网络，能够学习长期依赖关系。每个时间步的LSTM单位是矢量Rd的集合，其定义如下：

 

 ft表示遗忘因子、it表示输入因子，ot表示输出因子，Ct是一个储存单元，ht 是 hidden state；σ代表逻辑S型函数；

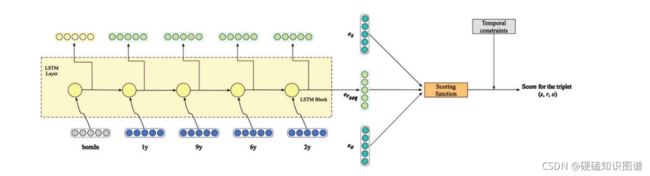
图3显示了我们如何利用LSTM学习时间感知表示。如图所示，我们首先通过线性层将时间戳的每个字符映射到向量。然后，将它们全部送入LSTM，并递归更新序列rseq的嵌入。我们将LSTM的最后一个隐藏状态作为最终输出,i.e.rseq=hN.最后，将包含时间信息的Rseq与现有的推理模型相结合。在本文中，我们采用TransR，因为它简单且性能良好，我们称之为TA -TransR。

TA -TransR的评分函数定义为：

 

 优化：如第3.2节所述。我们使用以下基于边缘的目标函数来训练我们的模型：

 其中ζ是正四元组，而ζ’是通过随机替换主体实体或客体实体构建的负四元组；

4.2.时间一致性约束

使用从上述模型获得的嵌入来预测缺失的事实仍然可能导致较差的性能。为了解决这个问题，我们对TA -TransR施加了三种时间一致性约束，并提出了一种ILP方法来消除结果中的错误预测。由于解决冲突的复杂性在很大程度上取决于所使用的制约因素，我们必须谨慎选择这些制约因素。

 Temporal disjointness

时间不相交约束要求共享同一关系的两个事实和一个共同的主体实体或客体实体之间的时间范围不应重叠。例如，在特定的时间范围内，一个男人不能成为两个不同女人的丈夫，(e1,
isHusbandOf,e2, [2003,2017])∧(e1,isHusbandOf,e3, [2010,2019])∧e2/=e3→False；时间不相交约束确保预测中的间隔位置在时间上不相交；约束可以表示为：

 Temporal ordering.

时间顺序约束要求某些关系应按时间顺序出现。 (e1,wasBornIn,e2,t1)∧(e1,worksAt,e3,t2)∧t1> t2→False;时间顺序约束表示关系对之间的依赖关系。它可以表示为:

 

时间跨度

有些事实只在一段时间内有效。如果给定的时间间隔不在有效时间间隔的范围内，则事实不正确；比如说, (e1,primeMinisterOf,e2,t‘) ，当时间间隔t'不在范围t内时无效,时间跨度约束确保一个间隔覆盖一组间隔中的这些间隔。

4.3. 整数线性规划公式

在本节中，我们将上述时间一致性约束添加到最终目标函数中，并将TKGR任务表述为ILP问题，

得到TA -TransRILP。对于每个事实 (s,rseq,o),，我们使用评分函数来表示通过先前的嵌入模型获得的其合理性，此外，一个布尔变量x定义事实（s、rseq、o）是否为真,为了在遵守所有时间约束的情况下最大化总体合理性，我们定义了以下目标函数：

 5. Experiments

在本节中，我们首先介绍用于评估的数据集。然后，我们在实体预测和关系预测任务上评估了我们的模型。

5.1.数据集集合

我们在YAGO11k和Wikidata12k数据集上进行实验，