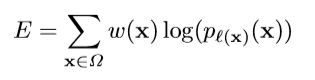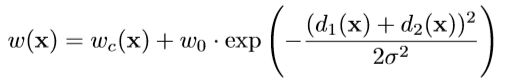从零开始的U-net入门
目录
前言
一、U-net基础知识
(1)ReLU函数
(2)图像的卷积和反卷积(上采样)
(3)池化层(下采样)
(4)损失函数
二、U-net入门
(1)U-net的结构是怎么样的?
(2)U-net的输入是什么?
(3)U-net的卷积核大小、卷积核数量、卷积核中的数值、训练深度怎么确定?
(4)如何解决U-net训练样本少的问题?
(5)U-net可以如何改进?
结语及U-net实现平台
前言
U-net是目前十分常用的人工智能图像分割算法,但是由于对深度学习接触得不是很深入,在看了许多直接从U-net结构开始解读的文章后仍存在不少疑问,在经过多天的阅读和思考后,按照自己的理解整理了一下U-net相关的基础知识以及常见问题的解答。本文整理的知识点大部分是通过阅读其他文章后再按照自己的理解进行总结的,在每个知识点最后会贴上对应链接,以方便查看更详细的说明。
首先放上U-net原文连接:
论文题目:U-Net: Convolutional Networks for Biomedical Image Segmentation
论文地址:https://arxiv.org/pdf/1505.04597v1.pdf
U-net是一个用于医学图像分割的全卷积神经网络。目前很多神经网络的输出结果都是最终的分类类别标签,但对医学影像的处理,医务人员除了想要知道图像的类别以外,更想知道的是图像中各种组织的位置分布,而U-net就可以实现图片像素的定位,该网络对图像中的每一个像素点进行分类,最后输出的是根据像素点的类别而分割好的图像。
一、U-net基础知识
(1)ReLU函数
ReLU函数实际上就是神经元的一种激活函数,简单来说,激活函数,并不是去激活什么,而是指把“激活的神经元的特征”通过某个函数把特征保留并映射到对应的分类标签上,即负责将神经元的输入映射到输出端。
ReLU函数的表达式很简单:
![]() (1)
(1)
图像如下:
从表达式可以看到ReLU函数实际上是一个取最大值的函数,从图像上则能看出该函数的作用是把大于0的数据都保留,而小于0的数据直接清零。这种“清零”实际上能够保证神经元的稀疏性,而这种“稀疏性”的好处则是能够降低计算量,并且能够防止过拟合,能够更好地挖掘图像特征。
选用ReLU函数作为激活函数的好处有以下几个:
①没有饱和区,不存在梯度消失问题。
②没有复杂的指数运算,计算简单、效率提高。
③实际收敛速度较快,比 Sigmoid/tanh 等激活函数快很多。
④比 Sigmoid 更符合生物学神经激活机制。
而缺点则是,当学习率过大的时候,可能造成大部分神经元清零死亡,即该神经元不会对任何数据有激活反应了。
相关链接:浅析激活函数之Relu函数
(2)图像的卷积和反卷积(上采样)
图像的卷积实际上是利用卷积核来对图像进行特征提取的一个过程。卷积核是一个矩阵,通过设计这个矩阵(如矩阵的大小、矩阵中的数值),就可以把相对应的图像特征提取出来,如图像的边缘特征、纹理特征等等。
下图展示的是一个3×3卷积核对图片的卷积过程:
来源: Convolutional Neural Networks - Basics · Machine Learning Notebook
图1中每一张图中间的3×3小正方形就是一个卷积核,左边是原始图像,而右边则是通过卷积后的结果,可以直观看到卷积的过程实际上就是把左边原图选定的3×3领域,与3×3的卷积核逐个数字对应相乘,最后把9个相乘后的结果相加,就是最终的卷积结果。我的理解是,卷积核实际上就是一系列具有特定分布的权重矩阵,通过对原图不同位置的像素点进行特定分布的加权,就能够提取卷积核所对应的一种图像特征。例如,这个卷积核本身就是边缘位置的权重分布较大,中间位置的权重分布较小(或直接设计为0),那么对原图进行卷积后,最后的结果就是提取出了原图的边缘特征。因此,我认为卷积核实际上就相当于一般全连接神经网络中的“权重”。
从上图可以看到,原图经过卷积后,结果图像比原图小了一圈,这是因为卷积核本身也有大小,导致原图的边缘信息没法完全卷积到所造成的。为了避免这种现象,在对图像进行卷积时,一般会先对原图进行扩大(一般是在图像周围加一圈0),以保证在卷积后的图像大小和原始图像相同,如图2所示:
来源卷积可视化工具箱: GitHub - vdumoulin/conv_arithmetic: A technical report on convolution arithmetic in the context of deep learning
从图2可以看到,在5×5原图(蓝色)的外面扩大一圈(白色)后,通过3×3卷积核卷积的结果图(绿色)能够同样保持5×5大小。
那如果把原图再往外扩大几圈呢?如图3所示:
来源卷积可视化工具箱: GitHub - vdumoulin/conv_arithmetic: A technical report on convolution arithmetic in the context of deep learning
从图3可以看出,把2×2原图扩大了两圈,再通过3×3的卷积核,卷积结果图像被增大为4×4的大小。
由以上所有结果可见,卷积其实一共有3种情况:
①卷积后,结果图像比原图小:称之为valid卷积
②卷积后,结果图像与原图大小相同:称之为same卷积
③卷积后,结果图像比原图大:称之为full卷积
其中,full卷积其实就是反卷积的过程。到这里应该可以意识到,反卷积实际上也是一种特殊的卷积方式,它可以通过full卷积将原图扩大,增大原图的分辨率,所以对图像进行反卷积也称为对图像进行“上采样”。因此,也可以很直接地理解到,图像的卷积和反卷积并不是一个简单的变换、还原过程,也就是先把图片进行卷积,再用同样的卷积核进行反卷积,是不能还原成原图的,因为反卷积后只是单纯地对图片进行扩大处理,并不能还原成原图像。图4所展示的例子可以很好地说明这一现象:
由图4可见,蓝色是3×3的卷积核,在原图进行卷积和反卷积后,最后得到的图像跟原图是不一致的。因此,通过反卷积并不能还原卷积之前的矩阵,只能从大小上进行还原,因为反卷积的本质还是卷积。如果想要还原成原图像,只能通过专门设计不同的卷积核来实现。
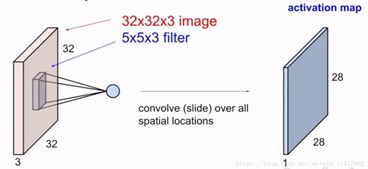
另外,在计算机中,灰度图像只有一个通道,而RGB图像有三个通道,如果需要对RGB图像进行卷积,效果则如图5所示:
图5中左边是一个32×32的RBG图像,因此整个图像大小为32×32×3,如果要对该图像进行卷积,图中5×5的卷积核大小则需要变成5×5×3,对图像的所有通道进行卷积,而卷积的结果会把这三层叠加起来,最终的结果图像大小为28×28×1(显然这是一个valid卷积)。由此可见,无论图像本身的通道有多少,一个卷积核只能得到一个通道的特征,也就是一个卷积核仅对应一种图像特征,若需要提取图像中的多种特征,则需要多个卷积核,如图6所示:
图6中选用了6个不同的卷积核,提取了图像中的6种特征,得到了右边的6个通道结果,每个特征通道的大小都为28×28×1。因此,需要提取多少个图像特征,就需要设计多少个不同的卷积核,这就是通常所说的卷积层。
相关链接1:彻底搞懂CNN中的卷积和反卷积
相关链接2:深度学习---图像卷积与反卷积(最完美的解释)
(3)池化层(下采样)
池化是一种减少参数的计算方法,而减少参数的方法就是直接把一些删除,池化层就是专门用于降低参数的处理层。池化一般分为最大池化和平均池化,我们更常用的是最大池化,具体运算如图7所示:
来源: 卷积神经网络概念与原理_yunpiao123456的博客-CSDN博客_卷积神经网络
其中池化核的大小也是根据想要删去的参数多少进行设计的。图5可以看到左边的4×4原图通过2×2的池化核进行池化后,减小成为2×2的图像。因此对图像进行池化,实际上就是对图像进行“下采样”。
相关链接:卷积层与池化层
(4)损失函数
损失函数Loss Function是用来估量模型的预测值与真实值的不一致程度,它是一个非负实值函数,损失函数越小,模型的训练效果越好,鲁棒性越强。这是神经网络在通过梯度下降等方法调整参数,使得训练结果不断逼近真实值时必须使用到的一个函数。U-net中使用的损失函数为带权重的交叉熵损失函数:
其中:
至于加权![]() 的原因,和U-net原文献中的分割任务有关,使用U-net对其他图片进行分割时可以不用该权重。(原文献中的U-net主要用于分割Hela细胞,为了加强粘连的同同类细胞之间的分割线而改进的损失函数,详细解释请看U-net原文。)
的原因,和U-net原文献中的分割任务有关,使用U-net对其他图片进行分割时可以不用该权重。(原文献中的U-net主要用于分割Hela细胞,为了加强粘连的同同类细胞之间的分割线而改进的损失函数,详细解释请看U-net原文。)
相关链接1:Softmax 函数的特点和作用是什么?
相关链接2:【深度学习】一文读懂机器学习常用损失函数(Loss Function)
二、U-net入门
(1)U-net的结构是怎么样的?
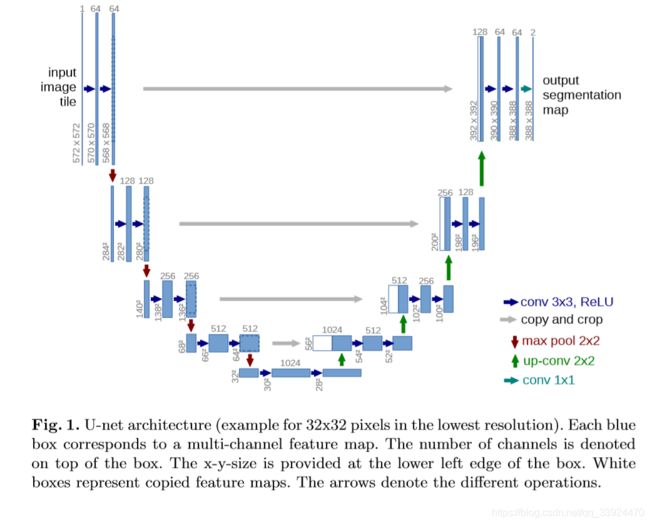
因为U-net的操作过程如“U”形,故而称为U-net,其具体结构如图8:
若已经理解前面U-net的基础知识,将能更好地看懂整个U-net的结构。首先看一下图例的含义:
①深蓝色箭头:利用3×3的卷积核对图片进行卷积后,通过ReLU激活函数输出特征通道;
②灰色箭头:对左边下采样过程中的图片进行裁剪复制;
③红色箭头:通过最大池化对图片进行下采样,池化核大小为2×2;
④绿色箭头:反卷积,对图像进行上采样,卷积核大小为2×2;
⑤青色箭头:使用1×1的卷积核对图片进行卷积。
该U-net网络一共有四层,分别对图片进行了4次下采样和4次上采样。由于结构部分数字比较多,过程比较繁琐,下面将按照自己的理解尽可能地把整个过程描述清楚。
从最左边开始,输入的是一张572×572×1的图片,然后经过64个3×3的卷积核进行卷积,再通过ReLU函数后得到64个570×570×1的特征通道。然后把这570×570×64的结果再经过64个3×3的卷积核进行卷积,同样通过ReLU函数后得到64个568×568×1的特征提取结果,这就是第一层的处理结果。
第一层的处理结果是568×568×64的特征图片,通过2×2的池化核,对图片下采样为原来大小的一半:284×284×64,然后通过128个卷积核进一步提取图片特征。后面的下采样过程也是以此类推,每一层都会经过两次卷积来提取图像特征;每下采样一层,都会把图片减小一半,卷积核数目增加一倍。最终下采样部分的结果是28×28×1024,也就是一共有1024个特征层,每一层的特征大小为28×28。
右边部分从下往上则是4次上采样过程。从最右下角开始,把28×28×1024的特征矩阵经过512个2×2的卷积核进行反卷积,把矩阵扩大为56×56×512(注意不是1024个卷积核,结果仅仅是右半边蓝色部分的512个特征通道,不包含左边白色的),由于反卷积只能扩大图片而不能还原图片,为了减少数据丢失,采取把左边降采样时的图片裁剪成相同大小后直接拼过来的方法增加特征层(这里才是左半边白色部分的512个特征通道),再进行卷积来提取特征。由于每一次valid卷积都会使得结果变小一圈,因此每次拼接之前都需要先把左边下采样过程中的图片进行裁剪。矩阵进行拼接后,整个新的特征矩阵就变成56×56×1024,然后经过512个卷积核,进行两次卷积后得到52×52×512的特征矩阵,再一次进行上采样,重复上述过程。每一层都会进行两次卷积来提取特征,每上采样一层,都会把图片扩大一倍,卷积核数目减少一半。最后上采样的结果是388×388×64,也就是一共有64个特征层,每一层的特征大小为388×388。
在最后一步中,选择了2个1×1的卷积核把64个特征通道变成2个,也就是最后的388×388×2,其实这里就是一个二分类的操作,把图片分成背景和目标两个类别。
(2)U-net的输入是什么?
由于在不断valid卷积过程中,会使得图片越来越小,为了避免数据丢失,在图像输入前都需要进行镜像扩大,如图9所示:
可以看到图像在输入前,四个边都进行了镜像扩大操作,以保证在通过一系列的valid卷积操作之后的结果能够与原图大小相一致。由于有些计算机的内存较小,无法直接对整张图片进行处理(医学图像通常都很大),会采取把大图进行分块输入的训练方式(如图9中的黄色框),最后将结果一块块拼起来。为了避免在拼接过程中边缘部分出现不连接等问题,在训练前,每一小块都会选择镜像扩大而不是直接补0扩大(如图9中的蓝色框),以保留更多边缘附近的信息。
(3)U-net的卷积核大小、卷积核数量、卷积核中的数值、训练深度怎么确定?
①U-net卷积核的大小为什么是3×3?
其实卷积核的大小是可以自己定义的,或者根据实验结果的优劣来进行选择。但一般的选择原则为卷积核越小越好,且一般为奇数×奇数的正方形。卷积核越小,能够大大地降低计算复杂性,但其中1×1的卷积核不具有提升感受野的作用,而卷积核为偶数×偶数时不能保证图片在进行same卷积操作后,还能够还原到原本的大小(会比原图多一条边/少一条边,自己画个图就明白了),因此通常选用3×3的卷积核。
②每一层的卷积核数量为什么是64→128→256→512→1024?
目前卷积核的数量也没有一个金标准,也是自己设置或者根据实验结果的好坏进行选择。但是卷积核过少会导致特征提取得不充分,导致训练效果差,而卷积核过多则会大大加大计算量,会存在过多冗余信息。在U-net浅层中,提取的一般是颜色、轮廓等比较浅显的图像特征,因此卷积核数量不需要特别多,而随着U-net训练层数越深,提取的很多都是图片中无法命名的抽象特征,因此需要更多的卷积核才能够把这些特征提取出来。而U-net每一层都会把卷积核数量翻一倍,是因为经过下采样后图片大小会变成原来的一半,因此认为卷积核应该增多一倍才能够更全面地提取图片特征。
③卷积核中的数值如何确定?
前面提到过,卷积核中的数值实际上就相当于是一般全连接神经网络中的权值,在全连接神经网络中,权值的确定一般都是经过“初始化→根据训练结果逐步调整→训练精度达到目标后停止调整→确定权值”这样一个过程,因此U-net卷积核中数值的确定过程也是类似的,一开始也是先用随机数(服从高斯分布)进行初始化,后面则根据前面提到的损失函数逐步对数值进行调整,当训练精度符合要求后停止,即能确定每个卷积核中的数值。而调整卷积核数值的过程,实际上就是U-net的训练过程,当卷积核结束训练确定数值后,则U-net训练完成,下面将可以用测试集来测试网络的鲁棒性和对新的图片进行分割预测。
④U-net训练深度如何确定?
这跟全连接神经网络中“神经网络层数如何确定”这样一个问题是类似的,目前也没有一个专门的标准,一般根据经验选取,或设置多种不同的深度,通过训练效果来选择最优的层数。U-net原文中也没有提到为什么要选择4层,可能是在该训练项目中,4层的分割效果最好。
相关链接:卷积神经网络的卷积核大小、卷积层数、每层map个数都是如何确定下来的呢?
(4)如何解决U-net训练样本少的问题?
医学影像数据存在一个共同的特点,就是样本量一般较少,当训练样本过少时,容易使得训练效果不佳。解决该问题的方法是数据增强,数据增强可以在训练样本较少时,也能够让神经网络学习到更多的数据特征,不同的训练任务,数据增强的方法也不尽相同。由于U-net文章中的任务是分割Hela细胞,作者选择了弹性变换的方式进行数据增强,如图10所示:
来源: U-Net论文详解_一个小迷糊66的博客-CSDN博客_unet网络结构详解
图10的弹性变换其实就是把原图进行不同的弹性扭曲,形成新的图片,扩大样本量,由于这种弹性变化在细胞中是十分常见的,人为增加这种数据量能够让U-net学习到这种形变的不变性,当遇到新的图像时候可以进行更好地分割。
(5)U-net可以如何改进?
①可以对U-net中的损失函数进行改进。损失函数有很多种,U-net原文中采用的是有权重的交叉熵损失函数,主要为了更好地分离粘连在一起的同类细胞设计的,如果分割的任务不同,也可以往损失函数中添加权重或进行其他的改进,以增强分割的准确性和鲁棒性。
②可以对U-net结构进行改进,如采用U-net++网络,如图11所示:
U-net++是在深度为4层的U-net基础上,把1~3层的U-net也全部组合到一起(图中左上角最小的三角形为深度为1层的U-net,第二个三角形为深度为2层的U-net,以此类推,把4个深度的U-net组合在一起),这个U-net++能够把每个深度的训练效果相互融合相互补充,可以对图像进行更为精确的分割。
相关链接1(强烈推荐,该文章的研究思维以及改进过程的思考十分值得学习):研习U-net
相关链接2(另一篇适合入门看的U-net文章,解释得比较简单易懂):U-Net+与FCN的区别+医学表现+网络详解+创新
结语及U-net实现平台
到此,基本就是花了一周时间学习的U-net资料整理。在AI Studio平台上有一个开放的U-net项目,可以通过在线修改和学习U-net的程序(python3),尝试跑了一下,数据预处理花了半小时,训练模型花了5小时,最后测试结果6小时左右(GPU情况下,当然是排除了各种奇怪的问题之后),若能亲自尝试一下,也不失为一种有意思的学习方法。
最后送上传送门:基于Paddle的肝脏CT影像分割
文章若有错误不妥之处,欢迎指出!