深度学习与PyTroch(三）

神经网络各层输出的可视化

ResNet-18，数字代表的是网络的深度，也就是说ResNet18 网络就是18层的吗？实则不然，其实这里的18指定的是带有权重的 18层，包括卷积层和全连接层，不包括池化层和BN层。
ResNet18的基本含义是，网络的基本架构是ResNet，网络的深度是18层。但是这里的网络深度指的是网络的权重层，也就是包括池化，激活，线性层。而不包括批量化归一层，池化层。

原始图片

from torchvision.models import resnet18
from torchvision import transforms
from PIL import Image
totensor=transforms.ToTensor()
toimg=transforms.ToPILImage()
net = resnet18(pretrained=True)
img=Image.open("dog.jpg")
img_tensor=totensor(img).unsqueeze(0)
img.show()

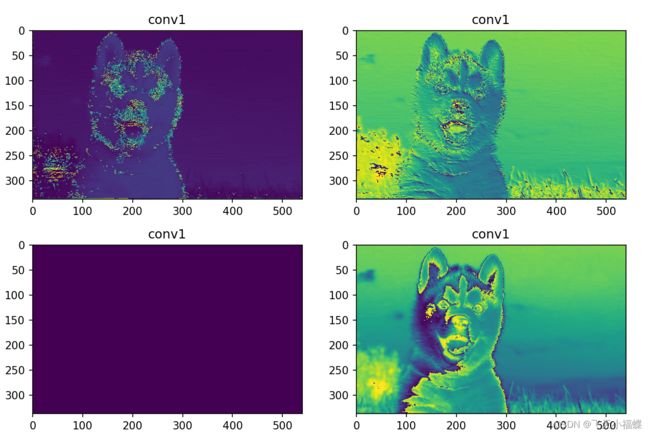
第一层卷积

f1=net.conv1(img_tensor)
plt.figure(figsize=(10,10))
print(f1)
# print(f1[0,1,:,:])
for p in range(4):
    f1_img_tensor=f1[0,p,:,:]
    f1_img = toimg(f1_img_tensor)
    plt.subplot(220+p+1)
    plt.imshow(f1_img)
    plt.title("conv1")
# plt.text("conv1",'y')
plt.show()

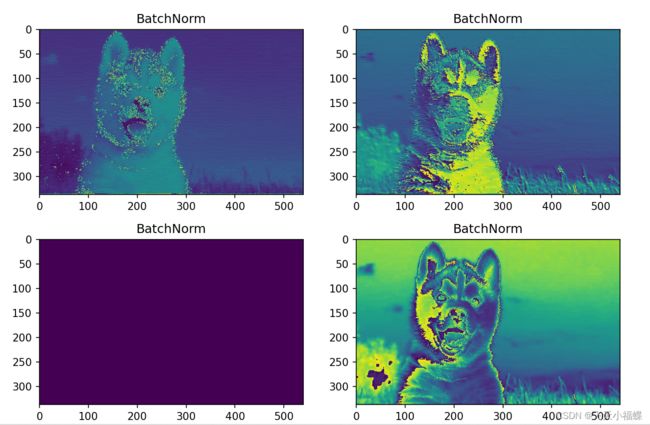
BatchNorm

f2=net.bn1(f1)
plt.figure(figsize=(10, 10))
for p in range(4):
    f2_img_tensor = f2[0, p, :, :]
    f2_img = toimg(f2_img_tensor)
    plt.subplot(220 + p + 1)
    plt.imshow(f2_img)
    plt.title("BatchNorm")
plt.show()

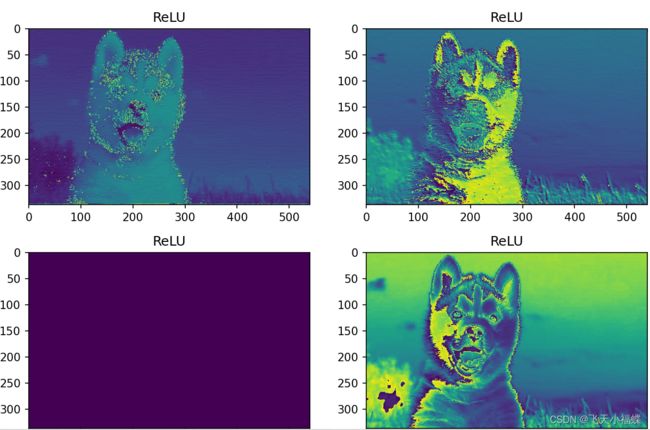
ReLU

f3 = net.bn1(f2)
plt.figure(figsize=(10, 10))
for p in range(4):
    f3_img_tensor = f3[0, p, :, :]
    f3_img = toimg(f3_img_tensor)
    plt.subplot(220 + p + 1)
    plt.imshow(f3_img)
    plt.title("ReLU")
plt.show()

循环神经网络

线性层搭配卷积层已经能很好地解决图像处理问题，但是在自然语言处理和时间序列预测方面，其效果却不如人意。有一个重要的原因就是线性层和卷积层的每一个输出都是相互独立的，也就是下一个输出不会受到上一个输出的影响，这显然不符合序列数据的特性。而循环神经网络(RNN）通过循环输入的方式，可以在两次输出之间建立联系，形成上下文通顺的预测结果。
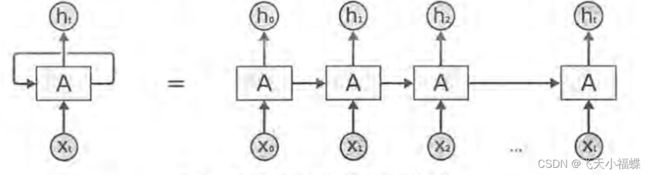
循环神经网络的来源是为了刻画一个序列当前的输出与之前信息的关系。从网络结构上，循环神经网络会记忆之前的信息，并利用之前的信息影响后面结点的输出。即：循环神经网络的隐藏层之间的结点是有连接的，隐藏层的输入不仅包括输入层的输出，还包括上一时刻隐藏层的输出。
循环神经网络对于每一个时刻的输入结合当前模型的状态给出一个输出。循环神经网络可以看做同一神经网络被无限复制的结果，出于优化考虑，现实生活中无法做到真正的无限循环。

损失函数

损失函数是描述模型预测值和真实值之间不一致程度的函数。神经网络的优化目标就是使损失函数越来越小，其中常用的主要是回归损失函数和分类损失函数，一些更复杂任务的损失函数可以通过修改或组合上述两类损失函数得到。
1、均方误差(MSE)

均方误差是指所有预测值和真实值之间的平方差，并将其平均值。常用于回归问题。

2、平均绝对误差(MAE)

作为预测值和真实值之间的绝对差的平均值来计算的。当数据有异常值时，这是比均方误差更好的测量方法。

3、均方根误差(RMSE)

这个损失函数是均方误差的平方根。如果我们不想惩罚更大的错误，这是一个理想的方法。
4、平均偏差误差(MBE)

类似于平均绝对误差但不求绝对值。这个损失函数的缺点是负误差和正误差可以相互抵消，所以当研究人员知道误差只有一个方向时，应用它会更好。

模型优化器optim

优化器就是在深度学习反向传播过程中，指引损失函数（目标函数）的各个参数往正确的方向更新合适的大小，使得更新后的各个参数让损失函数（目标函数）值不断逼近全局最小。
前向传播：通过输入层输入，一路向前，通过输出层输出的一个结果。如图指的是1 、 x1、x2、xn、与权重（weights）相乘，并且加上偏置值b0，然后进行总的求和，同时通过激活函数激活之后算出结果。这个过程就是前向传播。
反向传播：通过输出反向更新权重的过程。具体的说输出位置会产生一个模型的输出，通过这个输出以及原数据计算一个差值。将前向计算过程反过来计算。通过差值和学习率更新权重。
链接: https://blog.csdn.net/weixin_47286519/article/details/112278454

学习率

学习率是优化器中一个需要设定的参数，可以理解为每次更新参数时的步长。学习率选大了会导致结果溢出或振荡，选小了又会使模型的学习速度太慢或者局限于局部最优点。
学习速率代表了神经网络中随时间推移，信息累积的速度。学习率是最影响性能的超参数之一，如果我们只能调整一个超参数，那么最好的选择就是它。相比于其它超参数学习率以一种更加复杂的方式控制着模型的有效容量，当学习率最优时，模型的有效容量最大。因此，为了训练神经网络，其中一个需要设置的关键超参数是学习率。