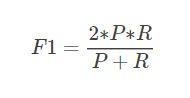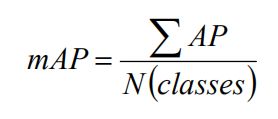nms和P，R，map原理及在Yolov5代码中的解析

         将非极大值抑制（nms）和map放在一块进行讲解分析，因为其都是通过IOU和置信度（score）来计算，但两者方式不一样，容易产生干扰，NMS通过IOU来过滤掉候选框，而map通过IOU来筛选正负样本。

目录

nms

所有类别nms

不同类别nms

准确率，召回率

F1和map

F1:

 Ap：       

Yolov5代码中P, R和Map解析

---

nms

       目标检测推理过程会产生许多目标检测框，这些检测框宽高都不一致，且每个检测框都赋有一个置信度阈值，需要对这些目标框进行过滤，筛选出最优的目标框。首先，通过事先设定好的置信度阈值可以过滤掉部分检测框（即置信度小于该阈值的检测框被过滤），置信度有两种形式，一种是前景的概率（即包含有物体的概率），另一种是前景概率与类别概率的乘积。对于剩余检测框通过NMS进行过滤，最终仅保留一个与目标最匹配的检测框。

        NMS有两种思路：

所有类别nms

伪代码算法简易步骤：

all_box = all_box.sort()  ## 将所有检测出的box从大到小进行排序

for i in len(all_box):       ## 根据置信度从大到小遍历所有的box

        for  j in len(all_box) :  ## 将置信度小于某个box的其他所有box与此box对比，计算IOU

                if j > i :

                        判断all_box[i]和all_box[j]的IOU面积是否大于阈值，如果大于阈值则删除此box，否则保留此box，直到所有box被保存，即为整张图片被检测到的所有目标框。

其原理图示如下，图片源于网络 Tom Hardy博客

 对所有类别进行nms，代码以python示例：

def NMS(boxes,scores, thresholds):
    x1 = boxes[:,0]
    y1 = boxes[:,1]
    x2 = boxes[:,2]
    y2 = boxes[:,3]
    areas = (x2-x1)*(y2-y1)
 
    _,order = scores.sort(0,descending=True)
    keep = []
    while order.numel() > 0:
        i = order[0]
        keep.append(i)
        if order.numel() == 1:
            break
        xx1 = x1[order[1:]].clamp(min=x1[i])
        yy1 = y1[order[1:]].clamp(min=y1[i])
        xx2 = x2[order[1:]].clamp(max=x2[i])
        yy2 = y2[order[1:]].clamp(max=y2[i])
 
        w = (xx2-xx1).clamp(min=0)
        h = (yy2-yy1).clamp(min=0)
        inter = w*h
 
        ovr = inter/(areas[i] + areas[order[1:]] - inter)
        ids = (ovr<=thresholds).nonzero().squeeze()
        if ids.numel() == 0:
            break
        order = order[ids+1]
    return torch.LongTensor(keep)

代码以nanodet的推理c++为例（仅部分）：

void nanodet::nms(std::vector& input_boxes, float NMS_THRESH)
{
    std::sort(input_boxes.begin(), input_boxes.end(), [](BoxInfo a, BoxInfo b) { return a.score > b.score; }); // 对检测的box根据置信度排序
    std::vector vArea(input_boxes.size());
    for (int i = 0; i < int(input_boxes.size()); ++i)
    {
        vArea[i] = (input_boxes.at(i).x2 - input_boxes.at(i).x1 + 1)
            * (input_boxes.at(i).y2 - input_boxes.at(i).y1 + 1);
    }  // 获取所有检测出的box的面积
    for (int i = 0; i < int(input_boxes.size()); ++i)
    {
        for (int j = i + 1; j < int(input_boxes.size());)
        {
            float xx1 = (std::max)(input_boxes[i].x1, input_boxes[j].x1);
            float yy1 = (std::max)(input_boxes[i].y1, input_boxes[j].y1);
            float xx2 = (std::min)(input_boxes[i].x2, input_boxes[j].x2);
            float yy2 = (std::min)(input_boxes[i].y2, input_boxes[j].y2);
            float w = (std::max)(float(0), xx2 - xx1 + 1);
            float h = (std::max)(float(0), yy2 - yy1 + 1);
            float inter = w * h;
            float ovr = inter / (vArea[i] + vArea[j] - inter); // IOU
            if (ovr >= NMS_THRESH)  // 从vector begin开始，置信度最大的box与另一box对比，如果IOU大于阈值则删除此box，进而和下一个box对比，直到所有box都对比完
            {
                input_boxes.erase(input_boxes.begin() + j);
                vArea.erase(vArea.begin() + j);
            }
            else
            {
                j++;
            }
        }
    }

        通过手动设置IOU阈值，容易产生两个主要问题，一是：当IOU阈值设置较大时，会有很多冗余的检测框不会被有效过滤；当IOU阈值设置较小，虽可有效过滤更多的检测框。但当有两个不同类别的物体相距很近时，另一个置信度较低的物体容易被过滤，从而无法被检测到；为了弥补这种缺陷往往会采用另一种方式。

不同类别nms

         通过不同类别进行NMS，伪代码算法步骤为：

for label in all_labels: 

        a. 获取此类别（label）下所有box信息   ## 坐标位置，置信度，类别概率

        b. 根据box置信度从高至低排序，保存且记录当前置信度最大box

        c. 遍历b中置信度最大box以外的其他所有box，对比其他所有box与置信度最大box的IOU，删除IOU大于阈值的其他box

        d. 对剩下box，重复循环b，c步骤

这种方法的缺陷为，当两个相同类别的物体相隔很近时，另一个被检测到置信度较低些的物体容易被过滤掉，结果仅保留此类别下的一种物体。图示如下，其中红框的犬只可以被有效检测到，但蓝框虚线犬只会被过滤，因为其IOU大于阈值。当然图示相隔还有一定距离，如果相隔更近，IOU就更大了，更加难以去除。

对于yolov5代码直接调用函数torchvision.ops.nms：

i = torchvision.ops.nms(boxes, scores, iou_thres)

对于多类别NMS的实现，通过对每个候选框坐标添加一个偏移量来实现，偏移量可以通过不同类别的索引来实现。源码如下：

max_coordinate = boxes.max()
offsets = idxs.to(boxes) * (max_coordinate + torch.tensor(1).to(boxes))
boxes_for_nms = boxes + offsets[:, None]
keep = nms(boxes_for_nms, scores, iou_threshold)
return keep

通过torchvision.ops.boxes.batched_nms(boxes, scores, classes, nms_thresh) 调用。

在yolov5中，实现代码：

        # Batched NMS
        c = x[:, 5:6] * (0 if agnostic else max_wh)  # classes 类别
        boxes, scores = x[:, :4] + c, x[:, 4]  # boxes (offset by class), scores

        ## 采用nms将框box数量过滤，IOU设置越小，框越少； i为经过nms后剩余框的索引
        i = torchvision.ops.nms(boxes, scores, iou_thres)  # NMS 将所有的框box，依据置信度scores得分进行过滤

 通过设置agnostic来判定是否使用多类别NMS，当agnostic为True时，即对所有类别进行NMS，当其为False时，对每个类别分开单独进行NMS。max_wh为检测框的最大宽高（像素），yolov5中指定为4096。

这两种方式的缺陷：①IOU阈值设置过大，，单个目标物会出现多个检测框，IOU阈值设置过小，则相邻的同类物体会被过滤掉；②低于IOU阈值的，置信度设置为0，不够合理；③NMS只能在CPU上运行，影响性能。

现方法中除了nms外还有soft nms可以从原理上有效解决多个同类别物体相隔很近时的检测问题。此外对于IOU的演化，还有GIOU,CIOU,DIOU以及最新的SIOU，其将两个不同box之间的距离，重叠率，尺度，横纵比等多维度进行考量。这些方法的改进思路和方法很简单，这里就不再赘述。

准确率，召回率

对准确性和召回率，通过TP，FP，FN三者的关系对准确性和召回率进行计算，对TP，FP，FN的解析如下：

TP:  与真实框的IOU大于设定阈值的检测框，被视为模型正确识别的正样本；

FP：与真实框的IOU小于设定阈值的检测框，被视为模型错误识别的正样本；

FN：没有被模型识别为正样本的目标（即模型没有检测到）

准确率和召回率计算公式为：

准确率（Precision）：

Precision=TP/(TP+FP)

表示模型预测的所有检测框中，预测正确的检测框（正样本数）所占的比例

召回率（Recall）：

Recall=TP/（TP+FN）

表示模型预测的所有检测框中，预测正确的检测框与实际真实框的比例

计算过程为：首先模型对所有验证集图片进行检测，通过NMS后保留下所有验证集图片的目标检测框。再基于设定的置信度阈值，对大于此阈值的检测框进行统计分析。

以如下图示和表为例：红色框为GT框，蓝色框，黑色框和黄色虚线框为检测框，

① 假定置信度阈值为0.3，三个检测框都大于设定的置信度阈值。另假定IOU阈值为0.6，其中蓝色框，黑色框与真实框IOU大于设定阈值，黄色虚线框与真实框IOU小于设定阈值，则TP=2（即被模型识别正确的检测框——蓝色框和黑色框），FP=1（被模型识别错误的检测框——黄色虚线框），FN=2（漏检的，左图红框中的犬只与右图下面犬只未被检测到），故准确率：Precision=2/(2+1)=0.67，召回率：Recall=2/(2+2)=0.5.

②假定置信度阈值为0.7，则置信度小于0.7的检测框不纳入统计范畴，IOU依旧阈值为0.6，则蓝色框和黄色虚线框作为检测框，TP=1(蓝色框)，FP=1（黄色虚线框），FN=3(四个GT框，仅蓝色框对应的GT框被检测到，其余三个为被检测到)，则准确率：Precision=1/(1+1)=0.5，Recall=1/(1+3)=0.25.

③假定置信度阈值为0.7，IOU阈值为0.4，基于置信度阈值，ID为1，2的两个框被检测到并作为统计，则：TP=2（蓝色框和黄色虚线框），FP=0，FN=2，Precision=2/(2+0)=1，Recall=2/(2+2)=0.5.

基于置信度从高至低排序：

目标ID| 检测框    |  置信度   | IOU
----------------------------
1     | 蓝色框    |  0.96    | 0.95
----------------------------
2     | 黄色虚线框|  0.75    | 0.42
----------------------------
3     |  黑色框   |  0.62    | 0.8

 总结：

        对准确率，召回率的计算，首先基于置信度阈值，选取置信度大于阈值的目标检测框，然后基于检测框和GT框的IOU，对IOU大于阈值的为预测正确的(TP），小于IOU阈值的为预测错误的(FP)，GT框中没有检测到的为漏检的(FN)。但基于准确率和召回率来衡量模型的性能效果，存在一定问题：通过手动设置置信度和IOU会存在人为因素偏差，针对不同的目标有不同的效果。故需要综合权衡准确率，召回率以及IOU的设置，一方面通过F1指标来权衡准确率和召回率，另一方面通过map来衡量。

F1和map

F1

F1的计算很简单，公式如下：

 Ap     

        Ap是衡量某一个类别检测效果的好坏。其根据不同的置信度和IOU阈值，对应有不同的准确率和召回率，进而通过计算准确率和召回率构成的二维曲线图面积即为Ap值。以官网图示为例：

在每个”峰值点”往左画一条直线，和上一个”峰值点”的垂直线相交，这样和坐标轴的面积就是AP值。 

 通过不同类别的Ap求取平均值即为mAP，其为衡量多个类别的检测效果：

         基于COCO的评价指标map，其IOU选择为0.5~0.95，间隔0.05，共10个IOU阈值，置信度固定为0.1或0.01，Yolov5源码中固定置信度阈值为0.1的一个线性插值，后面对Yolov5 map代码做讲解时分析。此外，其对Recall从0~1间隔0.1，分为101份小间隔，对这101个Recall对应的Precision值采用线性插值计算，最后通过计算所有这101个Recall和Precision值构成的小矩形面积，计算出Ap值。

Yolov5代码中P, R和Map解析

        以Yolov5源代码中对准确率，召回率，F1，Map的计算做展开讲解（每一行都有相对细节的文字解析）：

def ap_per_class(tp, conf, pred_cls, target_cls, plot=False, save_dir='precision-recall_curve.png', names=[]):
    # Sort by objectness
    i = np.argsort(-conf)  ## i 为基于所有验证集预测框的置信度的升序排序（因为添加了负号）, 获取升序后置信度对应的索引（将模型检测的所有验证集图片的box汇总一起）

    tp, conf, pred_cls = tp[i], conf[i], pred_cls[i]  ## tp为模型预测的每个框在10个IOU阈值下是否为正确的，其与GT框的IOU大于阈值则为True，否则为False，eg.tp ([ True  True  True  True  True  True  True  True  True False])；pred_cls为对应预测的类别(eg, pred_cls: [0,1,0,0]，即预测的类别分别为0，1，0，0)

    # Find unique classes 
    unique_classes = np.unique(target_cls)  # target_cls 真实的类别（eg,[0,1,0,1]）；unique_classes(唯一的类别顺序，即对所有GT框对应的类别从低到高排序且去重，例如：5个GT box对于类别[0,1,1,2,0],则unique_classes为[0,1,2])

    # Create Precision-Recall curve and compute AP for each class
    px, py = np.linspace(0, 1, 1000), []  # for plotting
    pr_score = 0.1  # score to evaluate P and R 指定固定置信度阈值https://github.com/ultralytics/yolov3/issues/898
    s = [unique_classes.shape[0], tp.shape[1]]  # number class, number iou thresholds (i.e. 10 for mAP0.5...0.95)
    ap, p, r = np.zeros(s), np.zeros(s), np.zeros(s) # p.shape:[类别数，10]，每一行表示每个类别，每一列代表每个IOU下的准确性（IOU：0.5~0.95）

    for ci, c in enumerate(unique_classes):   ## unique_classes 类别序号，如：0，1，2,... 0代表：猫，1代表狗，2代表鸟,...

        i = pred_cls == c  # i为基于预测的box列表中类别为c的索引处，当其IOU大于阈值为True，否则为False
        n_l = (target_cls == c).sum()  # number of labels, GT box列表中为类别c的数量加和，即类别c的GT框数量
        n_p = i.sum()  # number of predictions；预测的box列表中为类别c的数量加和，即预测类别c的预测框数量
        if n_p == 0 or n_l == 0:
            continue
        else:
            # Accumulate FPs and TPs  ;cumsum(0)，实现0轴（横轴）上的元素进行累加
            fpc = (1 - tp[i]).cumsum(0)  ## tp[i]的数组形状为[box数量，10]，每行为一个预测box，每列对应一个IOU下此box与GT box的布尔值（若大于IOU阈值为True，否则为False），通过1 - tp[i]获取预测box与GT box小于阈值的框，进而对所有预测box的True 或者False作累加。
            tpc = tp[i].cumsum(0)  ## 计算所有预测box与GT box的True或者False的累加值（IOU大于阈值为True） ，每一行为上一行到此行所有预测box的准确数或错误数累加和
            # Recall  r[ci] 
            recall = tpc / (n_l + 1e-16)  # recall curve
            # recall[:, 0] 为iou为0.5在所有预测框累加的召回率
            r[ci] = np.interp(-pr_score, -conf[i], recall[:, 0])  # r at pr_score, negative x, xp because xp decreases  基于各预测框置信度和召回率的对应（横轴，纵轴）关系，计算指定置信度阈值（0.1）下，采用线性插值法的召回率

            # Precision
            precision = tpc / (tpc + fpc)  # precision curve  -conf[i] [。。。]每个索引对应的置信度
            print('precision[:, 0]', precision[:, 0])
            p[ci] = np.interp(-pr_score, -conf[i], precision[:, 0])  # p at pr_score 计算方法和召回率一致

            # AP from recall-precision curve
            for j in range(tp.shape[1]):
                ap[ci, j], mpre, mrec = compute_ap(recall[:, j], precision[:, j])  ap的计算见下面分析
                if plot and (j == 0):
                    py.append(np.interp(px, mrec, mpre))  # precision at [email protected]
    # Compute F1 score (harmonic mean of precision and recall)
    f1 = 2 * p * r / (p + r + 1e-16)
    return p, r, ap, f1, unique_classes.astype('int32')

      对Yolov5代码整体过程简单分析：假设有5个预测box，6个gt box，置信度阈值和Yolov5一致设为0.1，IOU设置为0.5，对代码块

r[ci] = np.interp(-pr_score, -conf[i], recall[:, 0])

p[ci] = np.interp(-pr_score, -conf[i], precision[:, 0])

整体情况简析如下表：以第1，2行为例，预测box与gt box的IOU大于0.5为True，Recall=1/6=0.16, Precision=1/1=1，当rank为2，Recall=2/6=0.33, Precision=2/2=1，表格自上至下为Recall和Precision的累加形式。

Rank | box  |  -conf |GT(>0.5)| Recall | Precision
-----------------------------------------------
1    | Box1 |  -0.95|  True  | 0.16   |  1
-----------------------------------------------
2    | Box2 |  -0.90|  True  | 0.33   |  1
-----------------------------------------------
3    | Box3 |  -0.82|  False | 0.33   |  0.66
-----------------------------------------------
4    | Box4 |  -0.61|  True  | 0.50   |  0.75
-----------------------------------------------
5    | Box5 |  -0.05|  True  | 0.50   |  0.75
-----------------------------------------------

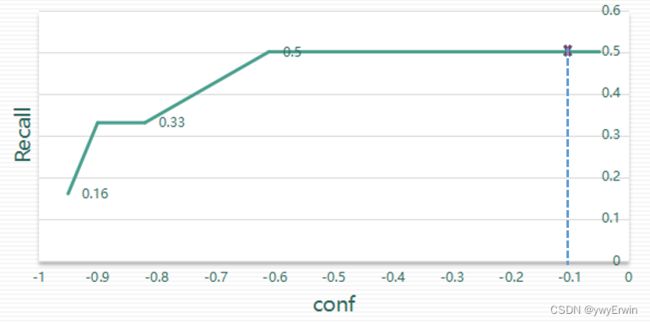
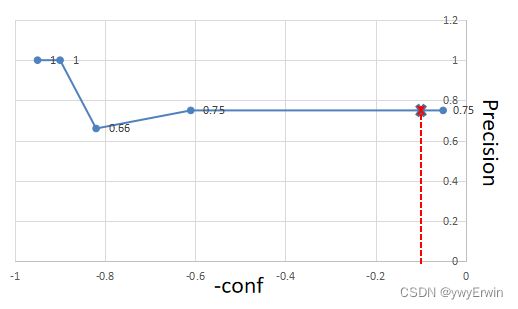
绘制-conf 和Recall，Precision曲线图，如下图所示，通过设置置信度阈值为0.1(和Yolov5源码设置的置信度一致)（则-conf为-0.1），计算其在-conf—Recall和-conf—Precision的线性插值，获取对应的准确率和召回率。

（注：上图横坐标应为-conf，保持与代码 -pr_score 一致）

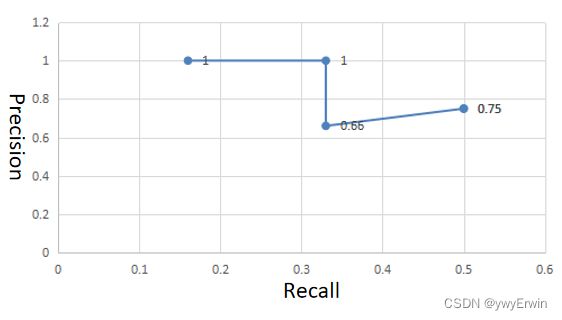
 其对应的Recall-Precision曲线图如下所示，图形与横轴围成的面积即为Ap值，同理当IOU为0.5~0.95中的任意一个时，其计算方式同IOU=0.5相同。此例子中Recall(iou=0.5)=0.50，Precision(IOU=0.5)=0.75.

        Yolov5中对Map的计算代码如下，其通过对纵坐标（Recall）分为101份，采用线性插值法计算每个Recall对应的Precision值，对所有101份Recall值和Precision围成的矩形计算面积加和，即为Ap：

def compute_ap(recall, precision):
    """ Compute the average precision, given the recall and precision curves
    # Arguments
        recall:    The recall curve (list)
        precision: The precision curve (list)
    # Returns
        Average precision, precision curve, recall curve
    """

    # Append sentinel values to beginning and end
    mrec = np.concatenate(([0.], recall, [recall[-1] + 0.01]))
    mpre = np.concatenate(([1.], precision, [0.]))

    # Compute the precision envelope
    mpre = np.flip(np.maximum.accumulate(np.flip(mpre)))

    # Integrate area under curve
    method = 'interp'  # methods: 'continuous', 'interp'
    if method == 'interp':
        x = np.linspace(0, 1, 101)  # 101-point interp (COCO) 设置将Recall分为101份
        ap = np.trapz(np.interp(x, mrec, mpre), x)  # integrate  # np.trapz计算x与mpre围成的面积之和； 采用np.interp(x, mrec, mpre)线性插值将基于横坐标（recall）的101个点基于线性插值，得出纵坐标（pre）的值
    else:  # 'continuous'
        i = np.where(mrec[1:] != mrec[:-1])[0]  # points where x axis (recall) changes
        ap = np.sum((mrec[i + 1] - mrec[i]) * mpre[i + 1])  # area under curve

    return ap, mpre, mrec

 Yolov5 test.py代码中（下述代码），p[:, 0], r[:, 0], ap[:, 0]，为IOU=0.5时的准确率，召回率和ap，纵列为10列IOU从0.5~0.95对应的值，若p[:,1]为IOU=0.55时的准确率，p[:,10]为IOU=0.95时的准确率。因为有多个类别，需要对其采用.mean()求取平均。

        p, r, ap50, ap = p[:, 0], r[:, 0], ap[:, 0], ap.mean(1)  # [P, R, [email protected], [email protected]:0.95]
        ## 计算了IOU从0.5到0.95时准确性和召回率分别为多少，并进行了平均值的计算
        mp, mr, map50, map = p.mean(), r.mean(), ap50.mean(), ap.mean()
        nt = np.bincount(stats[3].astype(np.int64), minlength=nc)  # number of targets per class