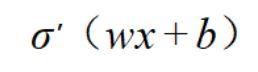深度网络梯度爆炸的原因、产生的影响和解决方法(常用激活函数)

1.概念

深度模型有关数值稳定性的典型问题是：衰减(vanishing)和爆炸(explosion)。

当神经网络的层数较多时，模型的数值稳定性容易变差。举个简单的例子：

为了便于讨论，不考虑偏差参数， 且设所有隐藏层的激活函数为恒等映射(identity mapping)φ(x) = x。给定输入X，多层感知机的第l层的输出H(l) = XW(1)W(2) ...W(l)。此时，如果层数l较大，H(l)的计算可能会出现衰减或爆炸。举个例子，假设输入和所有层的权重参数都是标量，如权重参数为0.2和5，多层感知 机的第30层输出为输入X分别与0.2^30 ≈ 1 × 10−21(衰减)和5^30 ≈ 9 × 1020(爆炸)的乘积。类似地，当层数较多时，梯度的计算也更容易出现衰减或爆炸。

简单说，权重参数小于1，会出现衰减，大于1，会出现爆炸。梯度消失和梯度爆炸本质上是一样的，都是因为网络层数太深而引发的梯度反向传播中的连乘效应。

梯度消失产生的影响：

会导致靠近输入层的隐藏层权值更新缓慢或者更新停滞。这就导致在训练时，只等价于后面几层的浅层网络的学习。

梯度爆炸产生的影响：

梯度爆炸一般出现在深层网络和权值初始化值太大的情况下，梯度爆炸会引起网络不稳定，最好的结果是无法从训练数据中学习，而最坏的结果是出现无法再更新的NaN权重值。

2.容易有数值稳定性问题的场景：

一是深度网络中，网络层数太多；从深层网络角度来讲，不同的层学习的速度差异很大，表现为网络中靠近输出的层学习的情况很好，靠近输入的层学习的很慢，有时甚至训练了很久，前几层的权值和刚开始随机初始化的值差不多。因此，梯度消失、爆炸，其根本原因在于反向传播训练法则，属于先天不足，另外多说一句，Hinton提出capsule的原因就是为了彻底抛弃反向传播，如果真能大范围普及，那真是一个革命。

梯度更新的速度：越靠近输出层，更新速度越快，越靠近输入层，更新速度越慢。原因：链式求导法则，越靠近输入层，链式越长，计算时间越多，因此越慢。

二是使用了不合适的激活函数，即非线性函数，比如sigmod函数，该函数的导数最大为0.25，再往后面网络传播的时候，很容易产生梯度消失。

事实上，梯度消失更容易出现，因为对于激活函数的求导：

可以看到，当w越大，其wx+b很可能变的很大，而根据最下面(手绘图)sigmoid函数导数的图像可以看到，wx+b越大，导数的值也会变的很小(导数曲线的最右边，当导数在0位置的时候，导数值最大为0.25)。因此，若要出现梯度爆炸，其w既要大还要保证激活函数的导数不要太小。

3.解决方法

1）预训练加微调

提出采取无监督逐层训练方法，其基本思想是每次训练一层隐节点，训练时将上一层隐节点的输出作为输入，而本层隐节点的输出作为下一层隐节点的输入，此过程就是逐层“预训练”（pre-training）；在预训练完成后，再对整个网络进行“微调”（fine-tunning）。Hinton在训练深度信念网络（Deep Belief Networks中，使用了这个方法。

2）梯度剪切、正则 

梯度剪切这个方案主要是针对梯度爆炸提出的，其思想是设置一个梯度剪切阈值，然后更新梯度的时候，如果梯度超过这个阈值，那么就将其强制限制在这个范围之内。这可以防止梯度爆炸。

权重正则化（weithts regularization）解决梯度爆炸。比较常见的是L1正则，和L2正则，在各个深度框架中都有相应的API可以使用正则化，比如在tensorflow中，若搭建网络的时候已经设置了正则化参数，调用layer层的时候，可以直接计算出正则损失。正则化是通过对网络权重做正则限制过拟合。

3）优化激活函数relu、leakrelu、elu

激活函数，就是在神经网络的神经元上运行的函数，负责将神经元的输入映射到输出端

Relu:思想也很简单，如果激活函数的导数为1，那么就不存在梯度消失爆炸的问题了，每层的网络都可以得到相同的更新速度，relu就这样应运而生。

relu的主要贡献在于：

-- 解决了梯度消失、爆炸的问题

-- 计算方便，计算速度快

-- 加速了网络的训练

同时也存在一些缺点：

-- 由于负数部分恒为0，会导致一些神经元无法激活（可通过设置小学习率部分解决）

-- 输出不是以0为中心的

leakrelu：

leakrelu就是为了解决relu的0区间带来的影响，其数学表达为：leakrelu=max(k∗x,x)leakrelu=max(k*x,x)leakrelu=max(k∗x,x)其中k是leak系数，一般选择0.01或者0.02，或者通过学习而来。leakrelu解决了0区间带来的影响，而且包含了relu的所有优点。

elu：

elu激活函数也是为了解决relu的0区间带来的影响。但是elu相对于leakrelu来说，计算要更耗时间一些。

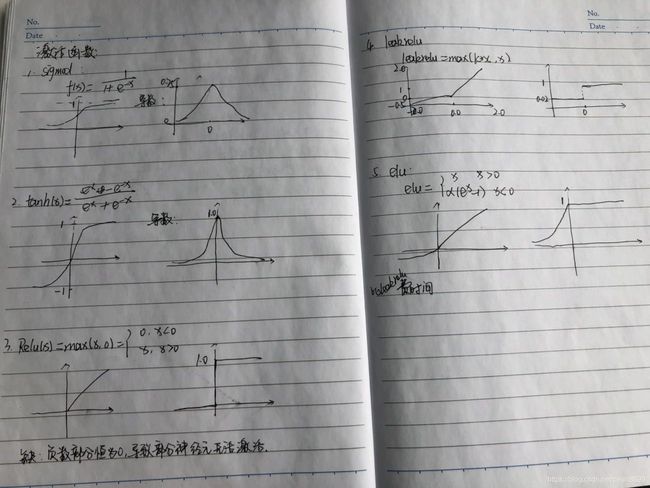
整理了一些激活函数的图以及其导数：

sigmoid和tanh激活函数有共同的缺点：即在z很大或很小时，梯度几乎为零，因此使用梯度下降优化算法更新网络很慢。

由于sigmoid和tanh存在上述的缺点，因此relu激活函数成为了大多数神经网络的默认选择。

但是relu也存在缺点：即在$z$小于0时，斜率即导数为0，因此引申出下面的leaky relu函数，但是实际上leaky relu使用的并不多。

4）batchnorm

Batchnorm是深度学习发展以来提出的最重要的成果之一了，目前已经被广泛的应用到了各大网络中，具有加速网络收敛速度，提升训练稳定性的效果，Batchnorm本质上是解决反向传播过程中的梯度问题。解决的过程：

f2​=f1​(wT∗x+b)对w求导，得到∂f2/∂w​​=∂f2/∂f1​ * ​​x，反向传播式子中有x的存在，所以x的大小影响了梯度的消失和爆炸，batchnorm就是通过对每一层的输出规范为均值和方差一致的方法，消除了x带来的放大缩小的影响，进而解决梯度消失和爆炸的问题，或者可以理解为BN将输出从饱和区拉倒了非饱和区。

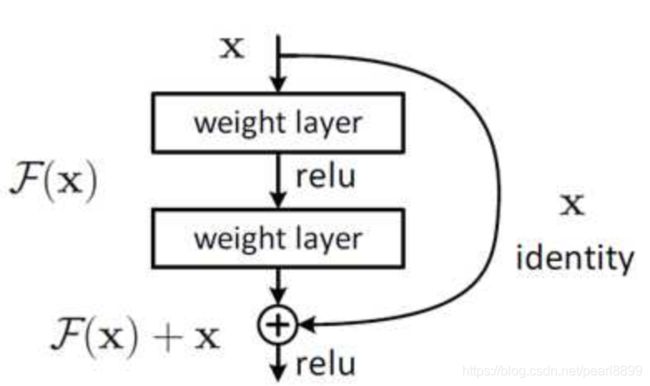
5）残差结构

残差可以很轻松的构建几百层，一千多层的网络而不用担心梯度消失过快的问题，原因就在于残差的捷径（shortcut）部分，其中残差单元如下图所示：

相比较于以前网络的直来直去结构，残差中有很多这样的跨层连接结构。这样传播过程中，不会存在梯度全为1的情况，不会梯度消失。

6）LSTM

LSTM全称是长短期记忆网络（long-short term memory networks），是不那么容易发生梯度消失的，主要原因在于LSTM内部复杂的“门”(gates)，LSTM通过它内部的“门”可以接下来更新的时候“记住”前几次训练的”残留记忆“。

参考：

1.梯度消失和爆炸的前世今生：详解机器学习中的梯度消失、爆炸原因及其解决方法_Double_V_的博客-CSDN博客_梯度消失和梯度爆炸

2.Deep Residual Learning for Image Recognition