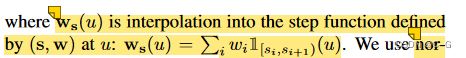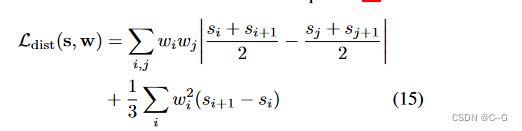16、Mip-NeRF360

简介

主页：https://jonbarron.info/mipnerf360/

Mip-NeRF通过基于圆锥体的渲染方式解决了原始NeRF对不同距离视角场景建模的混叠问题，并提高了渲染的速度，但是在关于无界场景的重建问题上，由于相机不规则的指向以及场景点的极远距离，使得Mip-NeRF的渲染效果还是有待改进。

将类似 NeRF 的模型应用于大型无界场景会引发三个关键问题：

• 参数化问题。mip-NeRF 要求将 3D 场景坐标映射到有界域，所以无界的 360 度的场景会占据无穷大的欧式空间区域。
• 效率问题。巨大且细节化的场景需要巨大的网络容量，所以在训练期间，频繁地沿每条射线去查询巨大的 MLP 网络会产生巨大的消耗 。
• 歧义问题。无界 360 度场景的背景区域明显比中心区域的光线稀疏。这种现象加剧了从 2D 图像重建 3D 内容的固有模糊性。

所以谷歌研究科学家Jon Barron又提出了关于无界场景重建的新的观点——Mip-NeRF 360，该论文从三个方面提出了新的观点，使用非线性场景参数化（non-linear scene parameterization）、在线“蒸馏”（online distillation）和新颖的基于失真的优化器（novel distortion-based regularizer）来克服无界场景带来的挑战。与 mip-NeRF 相比，均方误差降低了 57%，并且能够生成逼真的合成视图和详细的深度用于高度复杂、无界的现实世界场景的地图。

创新点

• 非线性场景参数化：提出一种类似卡尔曼滤波的方式将超出一定距离范围外的无界区域的高斯模型变换到非欧式空间中
• 在线“蒸馏”：若要令现有MLP去渲染无界场景，扩大网络结构的方式会降低渲染效率；因此在优化阶段，论文将网络分为两个：proposal MPL来优化权重参数，NeRF MLP来输出结果，这样在训练过程中，通过只优化proposal MLP来提高效率
• 基于失真的优化器：对于无界场景的渲染而言，会产生模糊的现象，即伪影；论文引入了一种优化器，针对基于圆锥体采样的渲染方式，最小化沿光线的所有点之间的加权绝对距离Ws（.）对重建场景中的伪影进行优化

实现流程

非线性场景参数化（non-linear scene parameterization）

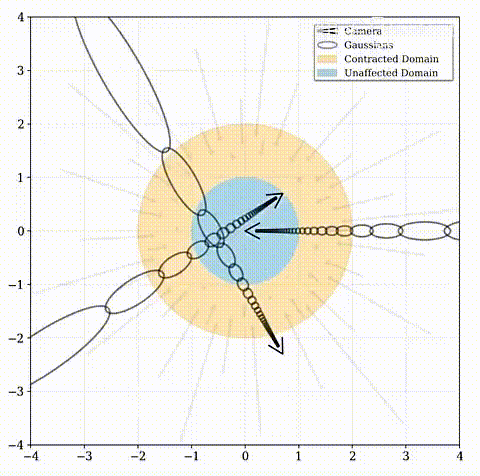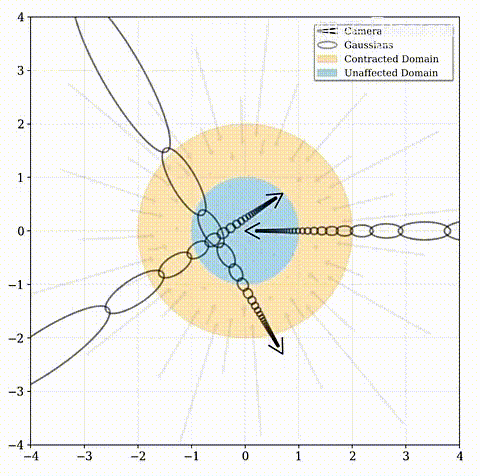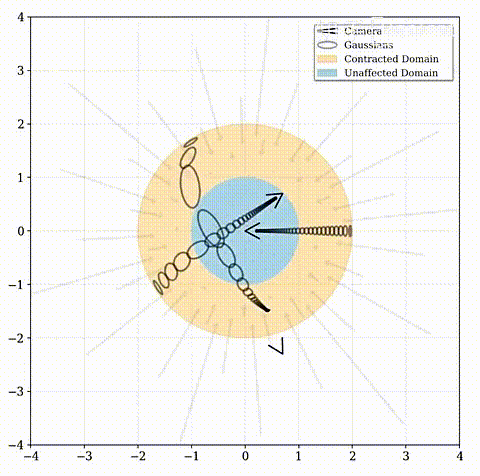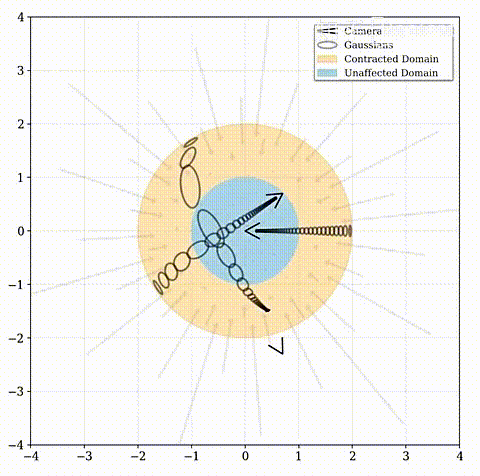
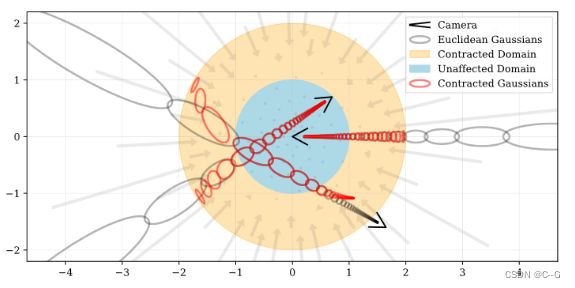
以一个有着三个摄像头的平地场景为例，在 mip-NeRF 中，这些相机将高斯函数投射到场景中。在一个大的场景，这导致高斯函数逐渐远离原点并且被拉长。这是因为 mip-NeRF 需要基于有界的坐标空间并且高斯函数在某种程度上是各向同性的

首先将f ( x )定义为从R n → R n （通常情况下n=3）映射的某个平滑坐标变换，然后可以计算这个函数的线性近似为

其中J f ( μ )是f 在μ处的雅可比矩阵。紧接着将( μ , Σ )高斯模型用f 转换：

这在功能上等同于经典的卡尔曼滤波器，其中f 是状态转移模型（state transition model）

远点应按视差（反距离）而不是距离成比例分布。该函数将坐标映射到半径为2（橙色）的球上，其中半径为1（蓝色）内的点不受影响。Mip-NeRF 360将这种收缩应用于欧氏三维空间中的基于圆锥体采样的高斯模型（灰色椭圆），类似于卡尔曼滤波器，以产生我们的Contracted高斯模型（红色椭圆），并且确保了其中心全部位于半径为2的球内。contract ( x ) 的设计结合了根据视差线性划分光线间隔的选择，意味着从位于场景原点的相机投射的光线在橙色区域将具有等距间隔。

论文还提出了一种选择光线距离t的方式——即根据视差参数化光线ray，随之定义了欧式光线距离t与“归一化”光线距离s之间的可逆映射

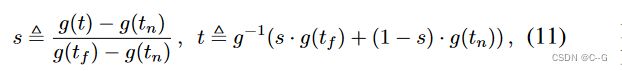
其中g ( ⋅ ) 是一个可逆的标量函数，文中取g ( x ) = 1 / x，这就给出了映射到[ t n , t f ] 的“归一化”光线距离s ∈ [ 0 , 1 ]，另一种说法为t-距离在视差中线性分布的射线样本。这很好地对应了原始NeRF中发挥有效作用的观点——在有界空间中均匀间隔的光线间隔（evenly-spaced ray intervals within a bounded space）

在线“蒸馏”（online distillation）

在 mip-NeRF 中，首先需要定义一组大致均匀分布的区间，可以理解为直方图中的端点。如图所示，每个间隔的高斯都被送入 mlp，并且得到直方图权重 w^c 和颜色 c^c。然后将这些颜色加权后得到像素点的颜色 C^c。之后这些权重被重采样，并得到一组新的区间，并且在场景中有内容的地方，端点就会较为聚集。

这个重采样可以多次进行，但为了方便在这里只显示一个。这个新的区间中的数据被送入同一 MLP 来得到一组新的权重和颜色，然后再通过加权得到像素点的颜色 C^f。mip-NeRF 只是最小化所有渲染像素值和输入图像真实像素值之间的重构损失。只有精细的颜色被用来渲染最终的图像是非常浪费的。

粗略渲染需要有监督学习来完成的唯一原因是帮助指导精细直方图的采样，这一观察激发了文中模型的训练和采样过程。研究者从一组均匀分布的直方图开始，将它们送入提出的 MLP 以产生一组权重，但不产生颜色。

这些权重会被重新采样，同样这个过程可以重复多次，但他们在视频中只展示了一个重采用过程。他们提出的 mlp 产生的最后一组区间被送入另一个 mlp，该 mlp 的行为与 mip-NeRF 中的完全相同，他们将其称为 NeRF mlp。NeRF mlp 为他们提供了一组可以用于渲染像素颜色的权重和颜色。

研究者将通过监督学习的方式，使得像素渲染得到的颜色接近真实图片中的颜色。他们让监督输出权重与 NeRF mlp 的输出权重一致，而不是监督文中提出的 mlp 来重建图像。这种设置意味着只需要经常去访问一个较小的 mlp，而较大的 NeRF mlp 则不需要太多的访问次数。

为了使模型起效，他们需要一个损失函数来鼓励具有不同区间划分的直方图彼此一致

左侧构建了一个真实的一维分布，在右侧的是两个该真实分布的直方图

因为这两个直方图刻画同一个分布，研究者可以对它们之间的关系做出一些强有力的断言，例如上面突出显示的那个区间的权重一定不会超过在下面的直方图中与其重叠的区间权重的总和。基于这个事实，他们可以使用一个直方图的权重来构造另一个直方图权重的上限


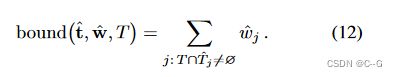
如果这两个直方图同时刻画相同的真实分布的，上界是必须确定的

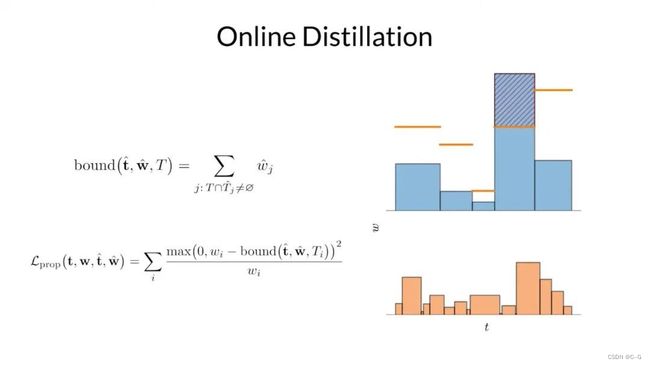
因此，在训练期间，研究者对他们提出的 mlp 和 NeRF mlp 分别生成的直方图之间构造了损失，该损失会惩罚任何违反此处以红色显示的边界的多余部分。通过这样方式，来鼓励他们提出的 mlp 学习什么是有效的上界。

基于失真的优化器（novel distortion-based regularizer）

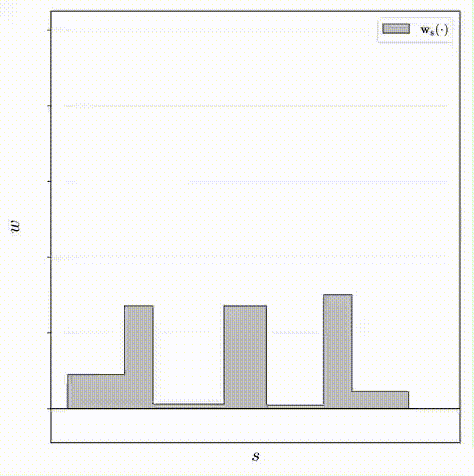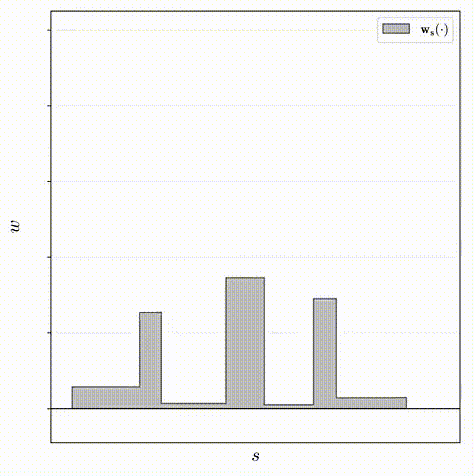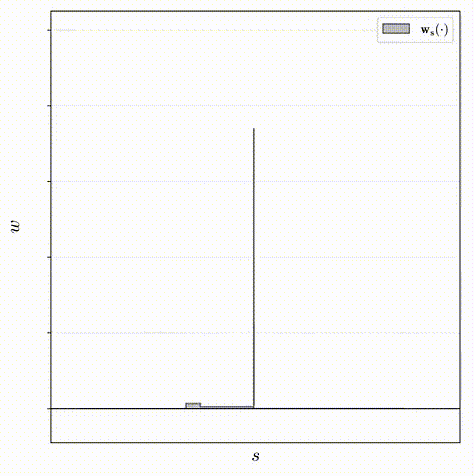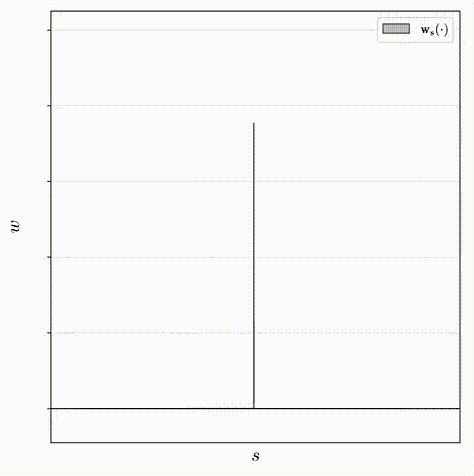
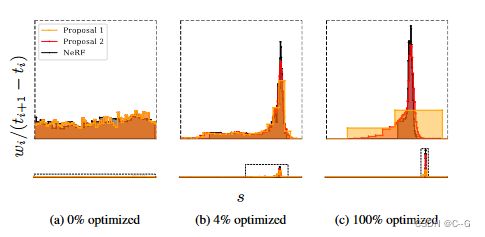
基于 nerf mlp 学习的体积场景密度，新模型中用来解决歧义问题的组件是光线直方图上的简单正则化器，他们简单地最小化沿光线的所有点之间的加权绝对距离，来鼓励每个直方图尽可能接近 delta 函数。这里显示的这个二重积分不容易计算，但可以推导出一个很好的封闭形式，计算起来很简单。

传统的NeRF经训练后会表现出两种模糊的现象：“floaters”——体积密集空间中的小而不相连的区域渲染后的结果像模糊的云一样、“background collapse”——远处的表面被错误地建模为靠近相机的密集内容的半透明云的现象。文章定义了一个优化器用来减少“floaters”和“background collapse”，该优化器的目的为最小化沿光线的所有样本之间的归一化加权绝对距离的值，即上图中所示的直方图的面积：

其中w s ( u )是在u 处对由( s , w )定义的阶跃函数（step function）的插值：w s ( u ) = ∑ i w i 1 [ s i , s i + 1 ) ( u )，但是上述公式不易计算，所以观察到w s ( u ) 在interval间离散的特性，将其离散化重写：