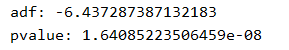arma模型_ARMA模型建模

ARMA(auto regression moving average)模型的全称是自回归移动平均模型，是目前最常用的拟合平稳序列的模型。它又可以细分为AR模型、MA模型和ARMA模型三大类，其中AR模型和MA模型实际上是ARMA模型的特例。本文以建立ARAM模型为例，学习如何使用Python进行时间序列分析。

下面针对Temperature.csv的差分序列建立ARAM模型，并对未来数据进行预测。数据集为1880-1985年全球气表平均温度改变值序列，总共106条记录。数据包含两个维度：年份和温度，数据格式如图1所示：

图1 部分训练样本示例

ARMA模型定阶原则

自相关系数	偏自相关系数	模型定阶
拖尾	p阶截尾	AR(p)模型
q阶截尾	拖尾	MA(q)模型
拖尾	拖尾	ARMA(p,q)模型

1.1  绘制时序图：

import pandas as pd import matplotlib.pyplot as plt  temp = pd.read_csv("Temperature.csv",index_col="year") temp.plot(kind="line",figsize=(12,6))  # 绘制折线图 plt.grid("on") plt.show()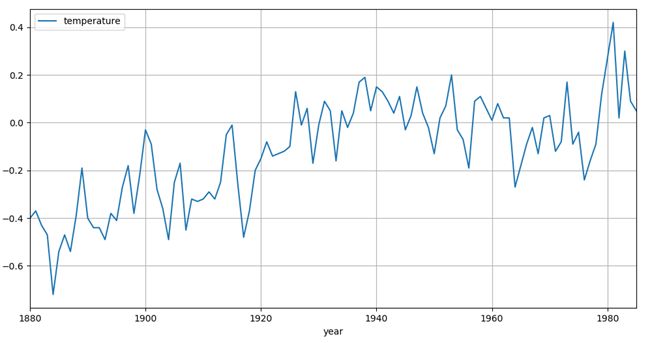

图2 全球气表平均温度改变值序列时序图

1.2一阶差分：

datadiff = temp.diff().dropna() # 对数据进行一阶差分 datadiff.plot(kind="line",figsize=(12,6))  # 将时间序列可视化 plt.grid("on") plt.title("diff data") plt.show()

使用temp.diff()方法对数据集进行差分，差分后得到的数据集的波动情况如下图所示：

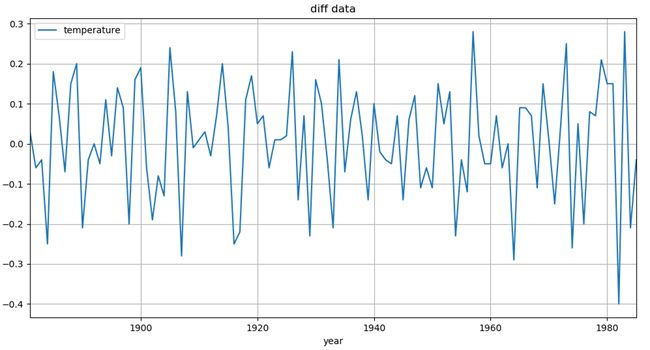
图3 全球气表平均温度改变值差分序列时序图

1.3  白噪声检验

时序图显示序列的波动非常稳定，再对差分后的数据进行白噪声检验，检验数据是否为随机序列。检验的原假设H0和备则假设H1分别如下：

H0：数据序列为白噪声，是随机数据；

H1：数据序列不是白噪声。

import statsmodels.api as smimport numpy as nplags = [4,8,12,16,20,24,28,32,36,64] LB = sm.stats.diagnostic.acorr_ljungbox(datadiff,lags=lags) LB = pd.DataFrame(data = np.array(LB).T,columns=["LBvalue","P-value"]) LB["lags"]=lags print("差分后序列的白噪声检验：\n",LB)

检验结果如下：

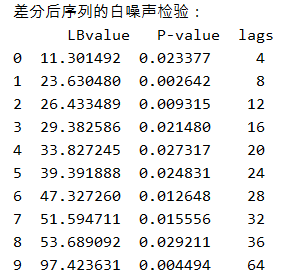
图4 白噪声检验结果

     白噪声检验使用sm.stats.diagnostic.acorr_ljungbox()函数。从上面的结果可以看出，在延迟阶数为[4,8,12,16,20,24,28,32,36,64]的情况下，LB检验的P值均小于阈值0.05，说明可以拒绝序列为白噪声的原假设，认为该数据不是随机数据，即该数据不是随机的，是有规律可循的，具有分析价值。

1.4  单位根检验

白噪声检验后，需要对数据平稳性进行判断，即对数据集进行单位根检验。检验数据的平稳性如下：

# 差分后序列的单位根检验，即检验序列的平稳性dftest = sm.tsa.adfuller(datadiff.temperature,autolag="AIC") print("adf:",dftest[0]) print("pvalue:",dftest[1])

输出结果如下：

使用sm.tsa.adfuller()函数进行单位根检验，输出结果为adf: -6.437287387132183，pvalue: 1.64085223506459e-08。因为P值远小于0.05，说明在置信度为95%的水平下，可以认为一阶差分后数据是平稳的。

下面将根据差分后的自相关图和偏相关图确定ARMA(p,q)模型的参数p和q。

1.5  绘制自相关图和偏相关图

fig = plt.figure(figsize=(10,5))   #差分后序列的自相关和偏自相关图ax1 = fig.add_subplot(211) fig = sm.graphics.tsa.plot_acf(datadiff,lags=60,ax=ax1) ax2 = fig.add_subplot(212) fig = sm.graphics.tsa.plot_pacf(datadiff,lags=60,ax=ax2) plt.subplots_adjust(hspace=0.3) plt.show()

使用graphics.tsa.plot_acf()函数得到自相关图，使用graphics.tsa.plot_pacf()函数得到偏自相关图，如下图所示。采用的数据均是差分后的平稳数据，lags=60表示延迟的阶数，也表示X轴的长度有60个刻度。

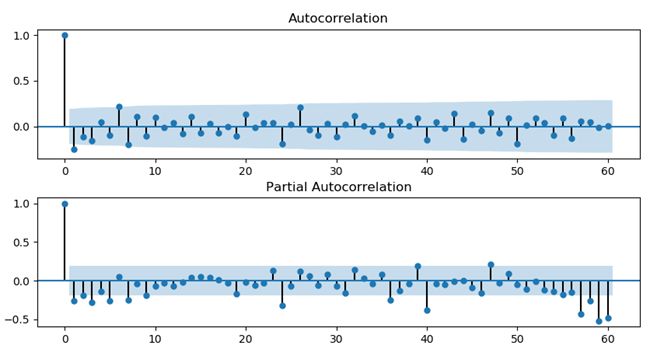
图5 自相关图和偏自相关图

由上图可知自相关系数和偏自相关系数均显示出不截尾的性质，因此可以使用ARMA(1,1)拟合该序列。

1.6  模型预测

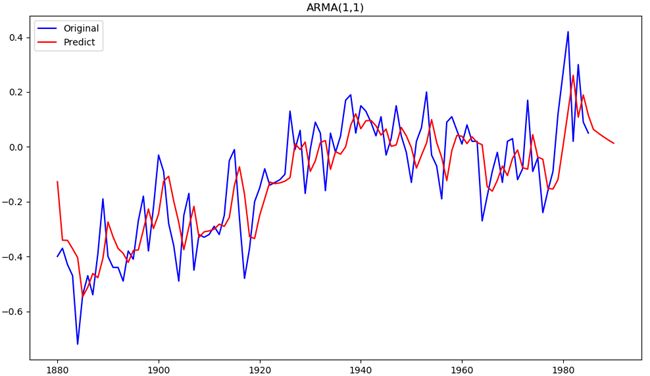
针对原始数据使用ARMA(1,1)进行预测。

ARMAmol = sm.tsa.ARMA(temp, order=(1,1)).fit() predicet_ARMA = ARMAmol.predict(start=0,end=110) predicet_ARMA.index = predicet_ARMA.index+1880 # 将原序列和预测序列绘制出来进行对比plt.figure(figsize=(12,8)) orig = plt.plot(temp,color="blue",label="Original") predict = plt.plot(predicet_ARMA,color="red",label="Predict") plt.title("ARMA(1,1)") plt.legend(loc="upper left") plt.show()

上面的代码使用sm.tsa.ARMA()建立模型后，使用fit()方法对数据进行拟合，并使用ARMAmol.predict()返回预测结果。调用predict函数时，原序列长度是106，将end设为110，会产生4个新的预测值。

图6 原序列和预测序列对比图

扫码关注我们 小白白AI学习