时序网络基础知识
时序网络基础知识
- RNN
-
- 前向传播
- 反向传播
- RNN缺点
- GRU
-
- GRU的前向传播
- 相较于LSTMGRU的优势
- LSTM
-
- LSTM的前向传播
- LSTM如何解决梯度消失
RNN
前向传播
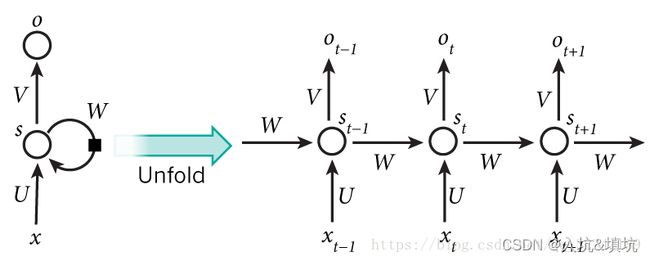
t t t、 t − 1 t-1 t−1、 t + 1 t+1 t+1为时间序列, s t s_t st表示样本在时间 t t t处的的记忆, s t = f ( W ∗ s t − 1 + U ∗ x t ) s_t=f(W*s_{t-1} +U*x_t) st=f(W∗st−1+U∗xt), W W W表示上一个时间记忆的输入权重, U表示此刻输入样本的权重, V表示输出的样本权重。
在 t = 1 t =1 t=1时刻, 一般初始化输入 s 0 = 0 s_0=0 s0=0, 随机初始化 W W W、 U U U、 V V V,进行下面的公式计算:
h t = U x t + W s t − 1 h_t=Ux_t+Ws_{t-1} ht=Uxt+Wst−1
s t = f ( h t ) s_t=f(h_t) st=f(ht)
o t = g ( V s t ) o_t=g(Vs_t) ot=g(Vst)
其中, f f f和 g g g均为激活函数,其中 f f f可以是 t a n h tanh tanh, r e l u relu relu, s i g m o i d sigmoid sigmoid等激活函数, g g g通常是 s o f t m a x softmax softmax也可以是其他。
注意:
- 这里的 W W W、 U U U、 V V V在每个时刻都是相等的(权重共享)。
- 隐藏状态可以理解为: s = f ( 现 有 的 输 入 + 过 去 记 忆 总 结 ) s=f(现有的输入+过去记忆总结) s=f(现有的输入+过去记忆总结)。
- 多层RNN只是多个RNN堆叠,一个RNN即一层,每一层的输出即为下一层的输入。
反向传播
参数的更新采用梯度下降法进行更新,也就是求每个参数的梯度。
每一次的输出值 O t O_t Ot都会产生一个误差值 e t e_t et, 则总的误差可以表示为: E = ∑ t = 1 n e t E=\sum_{t=1}^ne_t E=∑t=1net
d U = ∂ E ∂ U = ∑ t = 1 n ∂ e t ∂ o t ∂ o t ∂ s t ∂ s t ∂ U dU=\frac{\partial{E}}{\partial{U}}=\sum_{t=1}^n\frac{\partial{e_t}}{\partial{o_t}}\frac{\partial{o_t}}{\partial{s_t}}\frac{\partial{s_t}}{\partial{U}} dU=∂U∂E=∑t=1n∂ot∂et∂st∂ot∂U∂st
d V = ∂ E ∂ V = ∑ t = 1 n ∂ e t ∂ o t ∂ o t ∂ V t dV=\frac{\partial{E}}{\partial{V}}=\sum_{t=1}^n\frac{\partial{e_t}}{\partial{o_t}}\frac{\partial{o_t}}{\partial{V_t}} dV=∂V∂E=∑t=1n∂ot∂et∂Vt∂ot
d W = ∂ E ∂ W = ∑ t = 1 n ∂ e t ∂ o t ∂ o t ∂ s t ∂ s t ∂ W dW=\frac{\partial{E}}{\partial{W}}=\sum_{t=1}^n\frac{\partial{e_t}}{\partial{o_t}}\frac{\partial{o_t}}{\partial{s_t}}\frac{\partial{s_t}}{\partial{W}} dW=∂W∂E=∑t=1n∂ot∂et∂st∂ot∂W∂st
每个参数的梯度为它每个时刻的偏差的偏导数之和。
由于 t t t时刻的状态和 t − 1 t-1 t−1时刻的状态相关,所以 d U t 和 d W t dU_t和dW_t dUt和dWt为:
d θ t = ∂ e t ∂ o t ∂ o t ∂ s t ∂ s t ∂ θ = ∂ e t ∂ o t ∂ o t ∂ s t ( ∂ s t ∂ s 0 ∗ ∂ s 0 ∂ θ + ∂ s t ∂ s 1 ∗ ∂ s 1 ∂ θ + ⋯ + ∂ s t ∂ s t ∗ ∂ s t ∂ θ ) = ∂ e t ∂ o t ∂ o t ∂ s t ( ∑ i = 1 t ∂ s t ∂ s i ∗ ∂ s i ∂ θ ) d\theta_t=\frac{\partial{e_t}}{\partial{o_t}}\frac{\partial{o_t}}{\partial{s_t}}\frac{\partial{s_t}}{\partial{\theta}}=\frac{\partial{e_t}}{\partial{o_t}}\frac{\partial{o_t}}{\partial{s_t}}(\frac{\partial{s_t}}{\partial{s_0}}*\frac{\partial{s_0}}{\partial{\theta}}+\frac{\partial{s_t}}{\partial{s_1}}*\frac{\partial{s_1}}{\partial{\theta}}+\cdots+\frac{\partial{s_t}}{\partial{s_t}}*\frac{\partial{s_t}}{\partial{\theta}})=\frac{\partial{e_t}}{\partial{o_t}}\frac{\partial{o_t}}{\partial{s_t}}(\sum_{i=1}^t\frac{\partial{s_t}} {\partial{s_i}}*\frac{\partial{s_i}}{\partial{\theta}}) dθt=∂ot∂et∂st∂ot∂θ∂st=∂ot∂et∂st∂ot(∂s0∂st∗∂θ∂s0+∂s1∂st∗∂θ∂s1+⋯+∂st∂st∗∂θ∂st)=∂ot∂et∂st∂ot(∑i=1t∂si∂st∗∂θ∂si)
d V t dV_t dVt同理
出现梯度消失的原因:
∂ s t ∂ s i = ∂ s t ∂ s t − 1 ∗ ∂ s t − 1 ∂ s t − 2 ⋯ ∗ ∂ s i + 1 ∂ s i = ∏ k = i + 1 t ∂ s k ∂ s k − 1 \frac{\partial{s_t}}{\partial{s_i}}=\frac{\partial{s_t}}{\partial{s_{t-1}}}*\frac{\partial{s_{t-1}}}{\partial{s_{t-2}}}\cdots*\frac{\partial{s_{i+1}}}{\partial{s_{i}}}=\prod_{k=i+1}^t\frac{\partial{s_{k}}}{\partial{s_{k-1}}} ∂si∂st=∂st−1∂st∗∂st−2∂st−1⋯∗∂si∂si+1=∏k=i+1t∂sk−1∂sk
∂ s k ∂ s k − 1 = f ′ ∗ W \frac{\partial{s_{k}}}{\partial{s_{k-1}}}=f'*W ∂sk−1∂sk=f′∗W
∂ s t ∂ s i = ∏ k = i + 1 t f ′ ∗ W = ( f ′ W ) t − i − 1 \frac{\partial{s_t}}{\partial{s_i}}=\prod_{k=i+1}^tf'*W=(f'W)^{t-i-1} ∂si∂st=∏k=i+1tf′∗W=(f′W)t−i−1
当 f ′ ∗ W > 1 f'*W>1 f′∗W>1或 f ′ ∗ W < 1 f'*W<1 f′∗W<1时,如果i到t很长,则会出现梯度爆炸或消失,一般会使用梯度裁剪解决梯度爆炸问题,所以主要分析梯度消失问题。
l o s s loss loss对时间步 j j j的梯度值反映了时间步 j j j对最终输出 y t y_t yt的影响程度。就是 j j j对最终输出 y t y_t yt的影响程度越大,则 l o s s loss loss对时间步 j j j的梯度值也就越大。 l o s s loss loss对时间步 j j j的梯度值趋于0,就说明了 j j j对最终输出 y t y_t yt没影响。
综上:距离时间步t较远的j的梯度会消失, j j j对最终输出 y t y_t yt。
RNN缺点
- 每一时刻的预测只使用了之前的序列,没有使用之后的序列。
- 不擅长处理长期依赖的问题(序列后面的数据得到的序列前面数据的信息越少)。
- 深度神经网络可能存在梯度消失和爆炸的问题。
GRU
GRU是LSTM网络的一种效果很好的变体,它较LSTM网络的结构更加简单,而且效果也很好,因此也是当前非常流形的一种网络。GRU既然是LSTM的变体,因此也是可以解决RNN网络中的长依赖问题。
在LSTM中引入了三个门函数:输入门、遗忘门和输出门来控制输入值、记忆值和输出值。而在GRU模型中只有两个门:分别是更新门和重置门。具体结构如下图所示:
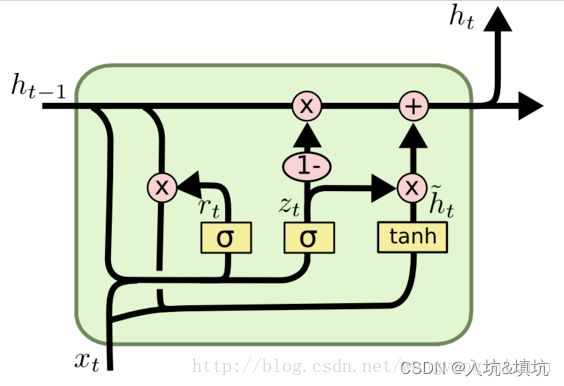
GRU的前向传播
r t = σ ( W r ⋅ [ h t − 1 , x t ] ) r_t=\sigma(W_r\cdot[h_{t-1},x_t]) rt=σ(Wr⋅[ht−1,xt])
z t = σ ( W z ⋅ [ h t − 1 , x t ] ) z_t=\sigma(W_z\cdot[h_{t-1},x_t]) zt=σ(Wz⋅[ht−1,xt])
h t ~ = t a n h ( W h ~ ⋅ [ r t ⨀ h t − 1 , x t ] ) \tilde{h_t}=tanh(W_{\tilde{h}}\cdot[r_t\bigodot h_{t-1},x_t]) ht~=tanh(Wh~⋅[rt⨀ht−1,xt])
h t = ( 1 − z t ) ⨀ h t − 1 + z t ⨀ h ~ h_t=(1-z_t)\bigodot h_{t-1}+z_t\bigodot\tilde{h} ht=(1−zt)⨀ht−1+zt⨀h~(进行遗忘和选择记忆, ( 1 − z t ) ⨀ h t − 1 (1-z_t)\bigodot h_{t-1} (1−zt)⨀ht−1对前面序列信息进行选择性遗忘, z t ⨀ h ~ z_t\bigodot\tilde{h} zt⨀h~对当前信息进行选择性记忆)
y t = σ ( W o h t ) y_t=\sigma(W_oh_t) yt=σ(Woht)
r r r:reset gate(重置门控)
z z z:update gate(更新门控)
相较于LSTMGRU的优势
GRU的参数量少,减少过拟合的风险
LSTM的参数量是Navie RNN的4倍(看公式),参数量过多就会存在过拟合的风险,GRU只使用两个门控开关,达到了和LSTM接近的结果。其参数量是Navie RNN的三倍
LSTM
LSTM中引入了三个门函数:输入门、遗忘门和输出门来控制输入值、记忆值和输出值
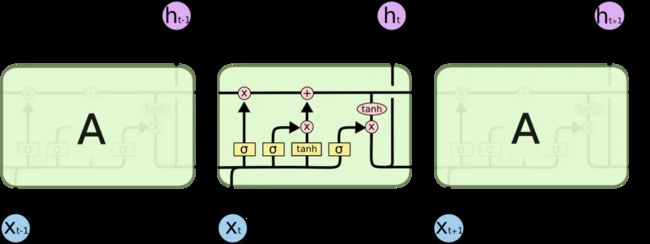
LSTM的前向传播
遗忘门: f t = σ ( W f ⋅ [ h t − 1 , x t ] + b f ) f_t=\sigma(W_f\cdot[h_{t-1},x_t]+b_f) ft=σ(Wf⋅[ht−1,xt]+bf)
其中 W f W_f Wf、 U f U_f Uf、 b f b_f bf为线性关系的系数和偏倚,和RNN中的类似。 σ \sigma σ为sigmoid激活函数。
输入门: i t = σ ( W i ⋅ [ h t − 1 , x t ] + b i ) i_t=\sigma(W_i\cdot[h_{t-1},x_t]+b_i) it=σ(Wi⋅[ht−1,xt]+bi), a t = t a n h ( W a ⋅ [ h t − 1 , x t ] + b a ) a_t=tanh(W_a\cdot[h_{t-1},x_t]+b_a) at=tanh(Wa⋅[ht−1,xt]+ba)
细胞更新: C t = C t − 1 ⨀ f t + i t ⨀ a t C_t=C_{t-1}\bigodot f_t+i_t \bigodot a_t Ct=Ct−1⨀ft+it⨀at
更新输出门输出: o t = σ ( W o ⋅ [ h t − 1 , x t ] + b o ) o_t=\sigma(W_o\cdot[h_{t-1},x_t]+b_o) ot=σ(Wo⋅[ht−1,xt]+bo), h t = o t ⨀ t a n h ( C t ) h_t=o_t\bigodot tanh(C_t) ht=ot⨀tanh(Ct)
更新当前序列索引预测输出: y ^ t = σ ( V h t + c ) \hat{y}_t=\sigma(Vh_t+c) y^t=σ(Vht+c)
GRU和LSTM反向传播算法的原理和RNN一样。
LSTM如何解决梯度消失
记忆细胞的连续偏导值为: ∂ C t ∂ C t − 1 = f t \frac{\partial{C_t}}{\partial{C_{t-1}}}=f_t ∂Ct−1∂Ct=ft
虽然 f t f_t ft是一个[0,1]区间的数值,不在满足当前记忆单元对上一记忆单元的偏导为常数。但通常会给遗忘门设置一个很大的偏置项,使得遗忘门在多数情况下是关闭的,只有在少数情况下开启。回顾下遗忘门的公式,这里我们加上了偏置b。
f t = σ ( W f ⋅ [ h t − 1 , x t ] + b f ) f_t=\sigma(W_f\cdot[h_{t-1},x_t]+b_f) ft=σ(Wf⋅[ht−1,xt]+bf)
趋向于1时,遗忘门关闭,趋向于0时,遗忘门打开。通过设置大的偏置项,使得大多数遗忘门的值趋于1。也就缓解了由于小数连乘导致的梯度消失问题。