《机器学习实战》9.树回归
目录
树回归
1 复杂数据的局部性建模
2 连续和离散型特征的树的构建
3 将CART算法用于回归
3.1 构建树
3.2 运行代码
4 树剪枝
4.1 预剪枝
4.2 后剪枝
5 模型树
6 示例:树回归与标准回归的比较
7 使用python的Tkinter库创建GUI
7.1 用Tkinter创建GUI
7.2 集成Matplotlib和tkinter
8 本章小结
本章涉及相关代码和数据
树回归
本章内容:
①CART算法
②回归与模型树
③树剪枝算法
④Python中GUI的使用
之前学习的线性回归很强大,但是这些方法创建的模型需要拟合所有的样本点。当数据众多特征并且特征之间的关系十分复杂时,构建全局模型的想法就比较困难,也略显笨拙。
一种可行的方法是将数据集切分成很多份易建模的数据,然后再进行线性回归,如果首次切分后仍然难以拟合线性模型就继续切分。在这种切分方式下,树结构和回归法就相当有用。
这里介绍一个新的叫做CART的树构建算法。该算法既可以分类又可以用于回归。
1 复杂数据的局部性建模
决策树是一种贪心算法,他要在给定书简被做出最佳选择,但并不关心是否能够达到全局最优
优点:可以对复杂和非线性的数据建模
缺点:结果不易理解
使用数据类型:数值型和标称型数据
之前学的树构建算法时ID3,他每次选取当前最佳的特征来分割数据,并按照该特征的所有特征值取值来切分。一旦按照某特征切分之后,该特征在之后的算法执行过程中将不再起作用,所以有观点认为这种切分方式过于迅速。
另一种方法时二元切分法,即每次把数据集切分为两份,如果数据的某特征值等于切分所要求的值,那么这些数据就进入树的左子树,反之则进入树的右子树,除了切分过于迅速之外,ID3算法还存在另一个问题,他不能直接处理连续性特征,只有事先将连续性数据转化为离散型,才可以使用,但这种转换会破坏连续型变量的内在性质。
使用二元切分法则易于对树构建过程进行调整已处理连续性数据。具体的处理方法时:1如果特征值大于给定值就走左子树,反之就走右子树。
树回归的一般方法:
①收集数据:采用任意方法收集数据
②准备数据:需要数值型数据,标称数据应该映射成二值型数据
③分析数据:会出数据的二维可视化显示结果,以字典的方法生成树
④训练算法:大部分书简都花费在u而节点树模型的构建上
⑤测试算法:使用测试数据上的R2值来分析模型的效果
⑥使用算法:使用训练出的树做预测,预测结果还可以用来做很多事情。
2 连续和离散型特征的树的构建
使用一个字典来存储树的数据结构特征,该字典将包含一下4个元素:
①待切分的特征,
②待切分的特征值,
③右子树:当不再需要切分的时候,也可以是单个值,
④左子树:与右子树类似
creatTree()的伪代码大致如下:
找到最佳的切分特征:
如果该节点不能再分,将该节点存为叶节点
执行二元切分
在右子树调用createTree()方法
在左子树调用createTree()方法
from numpy import *
# 回归树的切分函数
def regLeaf(dataSet):# 生成叶节点,因为在cart中就是求目标均值
# print(dataSet)
# print(dataSet[:,-1])
# return mean(list(dataSet[:,-1]))
return mean(dataSet[:,-1])
# 在给定数据上计算目标变量的平均误差
def regErr(dataSet): #
return var(dataSet[:,-1]) * shape(dataSet)[0]
# 加载数据
def loadDataSet(fileName):
# print(fileName)
dataMat=[]
fr=open(fileName)
for line in fr.readlines():
curLine=line.strip().split('\t')
# print(curLine)
# 将每行映射为浮点数
fltLine=list(map(float,curLine))
# print(fltLine)
dataMat.append(fltLine)
return dataMat
# 该函数将数据切分为两个子集并返回(二元切分法)
# 数据集合、待切分的特征、特征的某个值
def binSplitDataSet(dataSet,feature,value):
# nonzero函数用于得到数组array中非零元素的位置的函数
# 原书的代码,但运行出来有一点错误
# mat0=dataSet[nonzero(dataSet[:,feature]>value)[0],:][0]
# mat1=dataSet[nonzero(dataSet[:,feature]<=value)[0],:][0]
mat0=dataSet[nonzero(dataSet[:,feature]>value)[0],:]
mat1=dataSet[nonzero(dataSet[:,feature]<=value)[0],:]
# print(mat1)
# print(mat0)
return mat0,mat1
# 用最佳的方式切分数据集
def chooseBestSplit(dataSet, leafType=regLeaf, errType=regErr, ops=(1, 4)):
"""chooseBestSplit(用最佳方式切分数据集 和 生成相应的叶节点)
Args:
dataSet 加载的原始数据集
leafType 建立叶子点的函数
errType 误差计算函数(求总方差)
ops [容许误差下降值,切分的最少样本数]。
Returns:
bestIndex feature的index坐标
bestValue 切分的最优值
Raises:
"""
# ops=(1,4),非常重要,因为它决定了决策树划分停止的threshold值,被称为预剪枝(prepruning),其实也就是用于控制函数的停止时机。
# 之所以这样说,是因为它防止决策树的过拟合,所以当误差的下降值小于tolS,或划分后的集合size小于tolN时,选择停止继续划分。
# 最小误差下降值,划分后的误差减小小于这个差值,就不用继续划分
tolS = ops[0]
# 划分最小 size 小于,就不继续划分了
tolN = ops[1]
# 如果结果集(最后一列为1个变量),就返回退出
# .T 对数据集进行转置
# .tolist()[0] 转化为数组并取第0列
if len(set(dataSet[:, -1].T.tolist()[0])) == 1: # 如果集合size为1,不用继续划分。
# exit cond 1
return None, leafType(dataSet)
# 计算行列值
m, n = shape(dataSet)
# 无分类误差的总方差和
# the choice of the best feature is driven by Reduction in RSS error from mean
S = errType(dataSet)
# inf 正无穷大
bestS, bestIndex, bestValue = inf, 0, 0
# 循环处理每一列对应的feature值
for featIndex in range(n-1): # 对于每个特征
# [0]表示这一列的[所有行],不要[0]就是一个array[[所有行]]
for splitVal in set(dataSet[:, featIndex].T.tolist()[0]):
# 对该列进行分组,然后组内的成员的val值进行 二元切分
mat0, mat1 = binSplitDataSet(dataSet, featIndex, splitVal)
# 判断二元切分的方式的元素数量是否符合预期
if (shape(mat0)[0] < tolN) or (shape(mat1)[0] < tolN):
continue
newS = errType(mat0) + errType(mat1)
# 如果二元切分,算出来的误差在可接受范围内,那么就记录切分点,并记录最小误差
# 如果划分后误差小于 bestS,则说明找到了新的bestS
if newS < bestS:
bestIndex = featIndex
bestValue = splitVal
bestS = newS
# 判断二元切分的方式的元素误差是否符合预期
# if the decrease (S-bestS) is less than a threshold don't do the split
if (S - bestS) < tolS:
return None, leafType(dataSet)
mat0, mat1 = binSplitDataSet(dataSet, bestIndex, bestValue)
# 对整体的成员进行判断,是否符合预期
# 如果集合的 size 小于 tolN
if (shape(mat0)[0] < tolN) or (shape(mat1)[0] < tolN): # 当最佳划分后,集合过小,也不划分,产生叶节点
return None, leafType(dataSet)
return bestIndex, bestValue
# 数据集
def createTree(dataSet,leafType=regLeaf,errType=regErr,ops=(1,4)):
# 切分数据集
feat,val=chooseBestSplit(dataSet,leafType,errType,ops)
# 满足停止条件时返回叶节点值
if feat==None:
return val
retTree={}
retTree['spInd']=feat
retTree['spVal']=val
# 切分为左右两个子集
lSet,rSet=binSplitDataSet(dataSet,feat,val)
retTree['left']=createTree(lSet,leafType,errType,ops)
retTree['right']=createTree(rSet,leafType,errType,ops)
return retTree检查一下相关函数的运行结果
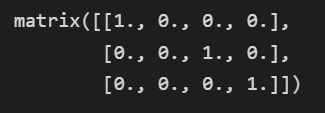
# 创建一个简单的矩阵
testMat=mat(eye(4))
testMat
# 测试函数
mat0,mat1=binSplitDataSet(testMat,1,0.5)
# print(mat0,mat1)
mat1运行结果为:
3 将CART算法用于回归
为了成功构建以分段常数为叶节点的树,需要度量出数据的一致性。
误差计算准则:
首先计算所有数据的均值,然后计算每条数据的值到均值的差值。为了对正负差同等看待,一般使用绝对值或者平方值来代替上述差值,这里需要计算平方误差的总值(总方差),总方差可以通过均方差乘以数据集中样本点的个数来得到。
3.1 构建树
上述代码还缺少一个ChooseBestSplit()函数:用最佳切分方式切分数据集和生成相应的叶节点
伪代码:
对每个特征:
对每个特征值
将数据切分成两份
计算切分的误差
如果当前误差小于当前最小误差,那么当前切分设定为最佳切分并更新最小误差
返回最佳切分的特征和阈值
上一节的函数调用了这里的代码,为了便于运行,该处的相关代码在上面代码段中体现。
3.2 运行代码
查看数据集中的数据分布
def plotDatalwlr(myMat):
import matplotlib.pyplot as plt
myMat=array(myMat)
fig=plt.figure()
ax=fig.add_subplot(111)
# ax.plot(xSort[:,1],yHat[srtInd])
ax.scatter(myMat[:,-2],myMat[:,-1],s=2,c='red')
plt.show()
myDat=loadDataSet('ex00.txt')
# print(myDat)
myMat=mat(myDat)
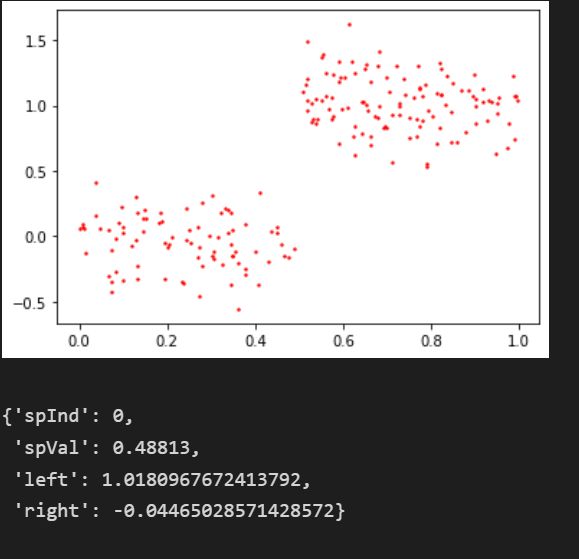
plotDatalwlr(myMat)
# myMat
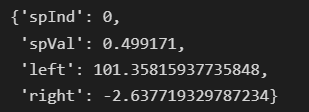
createTree(myMat)得到的数据中点的分布以及建成的树如下:
换另一种数据进行结果测试:
myDat1=loadDataSet('ex0.txt')
# myDat
myMat1=mat(myDat1)
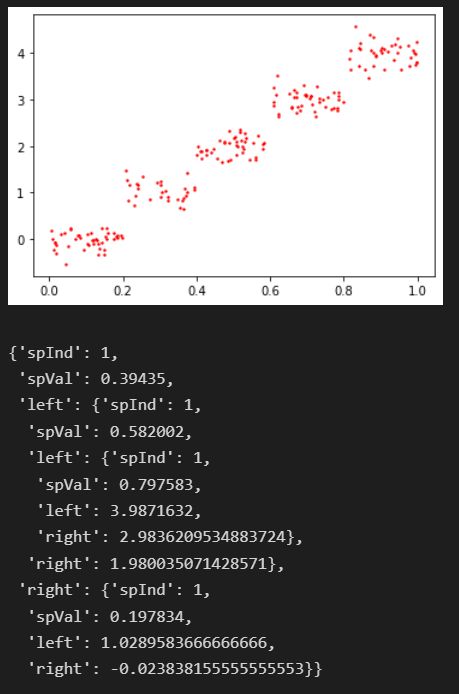
plotDatalwlr(myMat1)
# myMat
createTree(myMat1)得到的结果为:
到现在为止,已经完成回归树的构建,但是需要某种措施来检查构建过程是否得当。
下面将介绍树剪枝技术,它通过对决策树剪枝来达到更好的预测效果
4 树剪枝
一些树如果节点过多,表明该模型可能对数据进行了“过拟合”。
通过降低决策树的复杂度来避免过拟合的过程称为剪枝。
在函数ChooseBestSplit()中的提前终止条件,实际上是在进行一种所谓的预剪枝操作。
另一种形式的剪枝需要使用测试集和训练集,称为后剪枝
4.1 预剪枝
上面两个简单实验的结果还是令人满意的,但背后存在一些问题。树构建算法其实对输入的参数tolS和tolN非常敏感,如果使用其他值将不太容易达到这么好的效果。
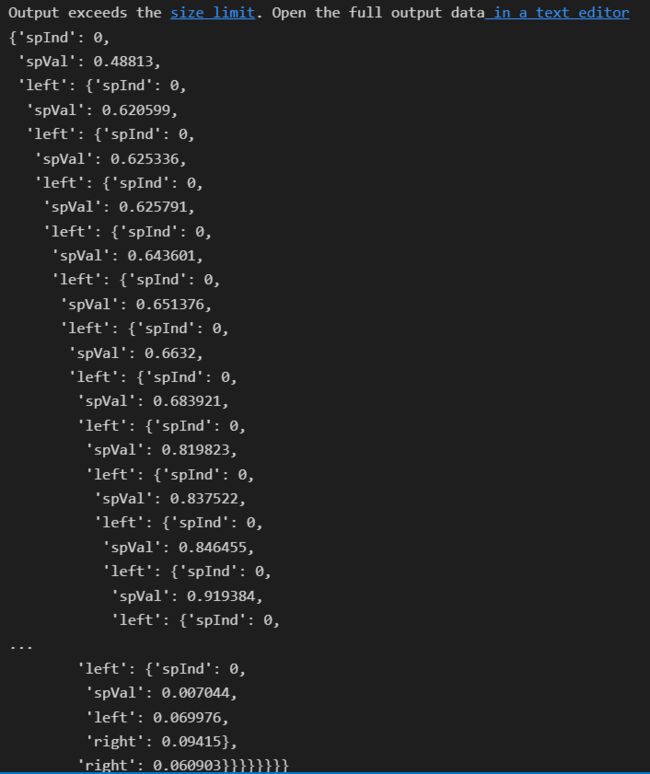
createTree(myMat,ops=(0,1))得到的输出结果为:
与上面只包含两个节点的树相比,这里构建的树过于臃肿,她甚至为数据集中的每个样本都分配了一个叶节点
下面数据集是上面数据集的100倍,用该数据来构建一颗新的树
myDat2=loadDataSet('ex2.txt')
myMat2=mat(myDat2)
plotDatalwlr(myMat2)
createTree(myMat2)得到的输出结果为:
第一个数据ex00.txt构建出来的树只有两个节点,但是这里构建的树则有很多叶节点,产生这个现象的原因在于,通停止条件tols对误差的数量级十分敏感。如果在选项中花费时间对上述误差容忍度取平均值,或许能够的都更好的结果。
createTree(myMat2,ops=(10000,4))得到的输出结果为:
通过不断修改停止条件来得到合理结果并不是很好的办法,因为我们常常不确定到底要什么样的结果。
因此因为不需要用户指定参数,后剪枝是一种更加理想的剪枝方法。
4.2 后剪枝
使用后剪枝方法需要将数据集分成测试集和训练集。首先指定参数,是的构建的树足够大、足够复杂,便于剪枝。接下来从上而下找到叶节点,用测试集来判断将这些叶节点合并是否能够降低测试误差。如果是的话就合并。
伪代码如下:
基于已有的树切分测试数据:
如果存在任一子集是一棵树,则在该子集递归剪枝过程
计算将当前两个叶节点合并后的误差
计算不合并的误差
如果合并会降低误差的话,就将叶节点合并
# 回归树剪枝函数
# 测试输入变量是否为一棵树
def isTree(obj):
# 判断该字段是否存在,返回bool类型的结果
return (type(obj).__name__=='dict')
def getMean(tree):
if isTree(tree['right']):
tree['right']=getMean(tree['right'])
if isTree(tree['left']):
tree['left']=getMean(tree['left'])
# 如果找到叶子节点就计算他们的平均值
return (tree['left']+tree['right'])/2.0
# 待剪枝的树 剪枝所需要的测试数据的平均值
def prune(tree,testData):
# 确认测试集是否为空
if shape(testData)[0]==0:
return getMean(tree)
if(isTree(tree['right'])or isTree(tree['left'])):
lSet,rSet=binSplitDataSet(testData,tree['spInd'],tree['spVal'])
if isTree(tree['left']):
tree['left']=prune(tree['left'],lSet)
if isTree(tree['right']):
tree['right']=prune(tree['right'],rSet)
if not isTree(tree['left']) and not isTree(tree['right']):
lSet,rSet=binSplitDataSet(testData,tree['spInd'],tree['spVal'])
errorNoMerge=sum(power(lSet[:,-1]-tree['left'],2))+sum(power(rSet[:,-1]-tree['right'],2))
treeMean=(tree['left']+tree['right'])/2.0
errorMerge=sum(power(testData[:,-1]-treeMean,2))
if errorMerge测试后剪枝的效果:
myTree=createTree(myMat2,ops=(0,1))
myDatTest=loadDataSet('ex2test.txt')
myMat2Test=mat(myDatTest)
prune(myTree,myMat2Test)
得到的输出结果为:
可以看到,大量的节点已经被剪枝掉了,但没有向预期那样简直成两部分,这说明后剪枝可能不如预剪枝有效。一般的,为了寻求最佳模型可以同时采用两追踪剪枝技术。
下面将重用部分已有的树构建代码来创建一种新的树。概述仍采用二元切分,但叶节点不再是简单的数值,取而代之的是一些线性模型。
5 模型树
用树来对数据建模,除了把叶节点简单的设定为常数值之瓦埃,还有一种方法是把叶节点设定为分段线性函数,这里所谓的分段线性是指模型由多个线性片段组成。
# 利用树的叶节点生成函数
# 将数据格式化成目标变量Y和自变量X,X和Y用于执行简单的线性回归
def linearSolve(dataSet):
m,n=shape(dataSet)
X=mat(ones((m,n)))
Y=mat(ones((m,1)))
X[:,1:n]=dataSet[:,0:n-1]
Y=dataSet[:,-1]
xTx=X.T*X
if linalg.det(xTx)==0.0:
raise NameError('This matrix is singular,cannot do inverse,\n try increasing the seccong value of ops')
ws=xTx.I*(X.T*Y)
return ws,X,Y
# 当数据不再需要切分的时候她负责生成叶节点的模型
def modelLeaf(dataSet):
ws,X,Y=linearSolve(dataSet)
return ws
# 在给定数据集上计算误差
def modelErr(dataSet):
ws,X,Y=linearSolve(dataSet)
yHat=X*ws
return sum(power(Y-yHat,2))查看数据分布
myMat2=mat(loadDataSet('exp2.txt'))
# print(myMat2)
plotDatalwlr(myMat2)得到的数据分布为:
创建树:
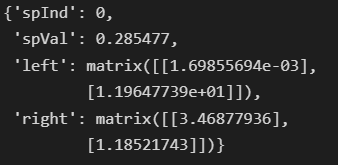
createTree(myMat2,modelLeaf,modelErr,(1,10))得到的模型树的结果为:
可以看到该代码以0.285477为界创建了两个模型。与实际数据非常数据接近。
模型树、回归树等比较哪个模型更好,一个比较客观的方法是计算相关系数R方,该系数可以通过调用命令corrcoef(yHat,y,rowvar=0)来求解
6 示例:树回归与标准回归的比较
# 用树回归进行预测的代码
# 对回归树叶节点进行预测
def regTreeEval(model,inDat):
return float(model)
# 对回归树树节点进行预测
def modelTreeEval(model,inDat):
n=shape(inDat)[1]
X=mat(ones((1,n+1)))
X[:,1:n+1]=inDat
return float(X*model)
# 返回一个浮点数,自顶向下遍历整棵树,直到命中叶节点为止
# 在给定树结构的情况下,对于单个数据点,该函数会给出一个预测值
def treeForeCast(tree,inData,modelEval=regTreeEval):
# 如果不是树,返回浮点值
if not isTree(tree):
return modelEval(tree,inData)
if inData[tree['spInd']]>tree['spVal']:
if isTree(tree['left']):
return treeForeCast(tree['left'],inData,modelEval)
else:
return modelEval(tree['left'],inData)
else:
if isTree(tree['right']):
return treeForeCast(tree['right'],inData,modelEval)
else:
return modelEval(tree['right'],inData)
def createForeCast(tree,testData,modelEval=regTreeEval):
# 拿到测试数据的长度
m=len(testData)
# 建立一个矩阵
yHat=mat(zeros((m,1)))
for i in range(m):
# 对每个节点进行预测
yHat[i,0]=treeForeCast(tree,mat(testData[i]),modelEval)
return yHat先查看数据的分布:
# 导入训练集与测试集,查看数据的分布
trainMat=mat(loadDataSet('bikeSpeedVsIq_train.txt'))
testMat=mat(loadDataSet('bikeSpeedVsIq_test.txt'))
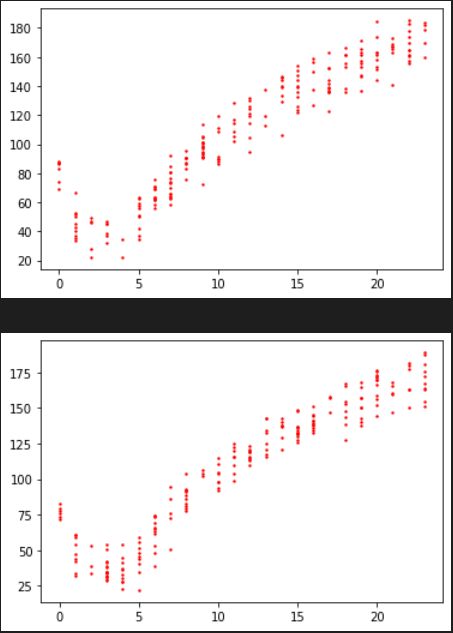
plotDatalwlr(trainMat)
plotDatalwlr(testMat)得到的输出图像为:
# 标准回归
myTree=createTree(trainMat,ops=(1,20))
yHat=createForeCast(myTree,testMat[:,0])
corrcoef(yHat,testMat[:,1],rowvar=0)[0,1]
# 同样的在创建一棵树回归
myTree=createTree(trainMat,modelLeaf,modelErr,(1,20))
yHat=createForeCast(myTree,testMat[:,0],modelTreeEval)
corrcoef(yHat,testMat[:,1],rowvar=0)[0,1]
得到的输出结果为:
![]()
![]()
我们知道R方越接近1越好,所以从上面的结果可以看出,这里模型树的结果比回归树好
为了得到测试集上的所有yHat预测值,在测试数据上循环执行
我们尝试一下单纯的线性回归
# 进行单纯的线性回归
ws,X,Y=linearSolve(trainMat)
for i in range(shape(testMat)[0]):
yHat[i]=testMat[i,0]*ws[1,0]+ws[0,0]
corrcoef(yHat,testMat[:,1],rowvar=0)[0,1]得到的输出结果为:
![]()
可以看到,该方法在R方值的表现上不如上面那两种树回归的方法。因此,树回归方法在预测复杂数据上时回避简单的线性模型更有效。
下面使用python提供的框架来构建图像用户界面(GUI)
7 使用python的Tkinter库创建GUI
机器学习给我们提供了一些强大的工具,能从未知数据中抽取出有用的信息。因此,能否将这些信息以易于人们理解的方式呈现十分重要。再者,加入人们可以直接与算法和数据进行交互,将可以比较轻松的进行解译。如果仅仅知识绘制出一幅静态图像,或者知识在python命令行中输出一些数字,那么对结果做分析和交流非常困难。能过能够让用户不需要任何指令就可以按照他们自己的方式来分析数据,就不需要对数据做过多的解释。其中一个能同时支持数据呈现和用户交互的方式就是构建一个图形用户界面GUI
示例:利用GUI对回归树进行调优
①收集数据:所提供的文本文件
②准备数据:用python解析上述文件,得到数值型数据
③分析数据:利用Tkinter构建一个GUI来展示模型和数据
④训练算法:训练一棵回归树和一颗模型树,并与数据一起展示出来
⑤测试算法:这里不需要测试过程
⑥使用算法:GUI使得人们可以在预剪枝时测试不同参数的影响,还可以帮助我们选择模型的类型
7.1 用Tkinter创建GUI
python有很多GUI框架,其中一个易于使用的Tkinter,是随python的标准编译版本发布的。Tkinter可以在多平台上运行,下面从一个简单的例子开始
from tkinter import *
root=Tk()
myLabel=Label(root,text="helo world")
myLabel.grid()
# 启动事件循环,使得该窗口可以响应鼠标点击、按键和重绘等操作
root.mainloop()运行得到:
# 用于构建树管理器界面的tkinter小部件
def reDraw(tolS,tolN):
pass
def drawNewTree():
pass
root=Tk()
# grid()函数设定行和列的位置
Label(root,text='plot place holder').grid(row=0,columnspan=3)
Label(root,text='tolN').grid(row=1,column=0)
tolNentry=Entry(root)
tolNentry.grid(row=1,column=1)
tolNentry.insert(0,'10')
Label(root,text='tolS').grid(row=2,column=0)
tolNentry=Entry(root)
tolNentry.grid(row=2,column=1)
tolNentry.insert(0,'1.0')
Button(root,text='ReDraw',command=drawNewTree).grid(row=1,column=2,rowspan=3)
chkBtnVar=IntVar()
chkBtn=Checkbutton(root,text="model Tree",variable=chkBtnVar)
chkBtn.grid(row=3,column=0,columnspan=2)
# 退出按钮
Button(root,text='Quit',fg='black',command=root.quit).grid(row=1,column=2)
reDraw.rawDat=mat(loadDataSet('sine.txt'))
reDraw.testDat=arange(min(reDraw.rawDat[:,0]),max(reDraw.rawDat[:,0]),0.01)
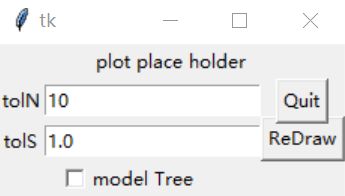
reDraw(1.0,10)
root.mainloop()运行得到:
7.2 集成Matplotlib和tkinter
import matplotlib
matplotlib.use('TkAgg')
from matplotlib.backends.backend_tkagg import FigureCanvasTkAgg
from matplotlib.figure import Figure
def reDraw(tolS,tolN):
# 清空?
reDraw.f.clf()
reDraw.a = reDraw.f.add_subplot(111)
# 检查复选框是否被选中
if chkBtnVar.get():
if tolN < 2:
tolN = 2
# 创建模型树
myTree = createTree(reDraw.rawDat, modelLeaf, modelErr, (tolS, tolN))
yHat = createForeCast(myTree, reDraw.testDat, modelTreeEval)
else:
# 否则创建回归树
myTree = createTree(reDraw.rawDat, ops = (tolS, tolN))
yHat = createForeCast(myTree, reDraw.testDat)
reDraw.a.scatter(array(reDraw.rawDat[:, 0]), array(reDraw.rawDat[:, 1]), s=5)
# reDraw.a.scatter(reDraw.rawDat[:,0],reDraw.rawDat[:,1],s=5)
reDraw.a.plot(reDraw.testDat,yHat,linewidth=2.0)
reDraw.canvas.draw()
# 理解用户输入内容
def getInputs():
try:
tolN = int(tolNentry.get())
except:
tolN = 10
print("enter Integer for tolN")
tolNentry.delete(0,END)
tolNentry.insert(0,'10')
try:
tolS = float(tolSentry.get())
except:
tolS = 1.0
print("enter Float for tolS")
tolSentry.delete(0,END)
tolSentry.insert(0,'1.0')
return tolN,tolS
def drawNewTree():
# 得到用户输入的数值
tolN,tolS = getInputs()
# 重新画出拟合的直线
reDraw(tolS,tolN)
root = Tk()
Label(root,text="Plot Place Holder").grid(row = 0,columnspan=3)
Label(root,text="tolN").grid(row=1,column=0)
tolNentry = Entry(root)
tolNentry.grid(row = 1,column=1)
tolNentry.insert(0,'10')
Label(root,text='tolS').grid(row=2,column=0)
tolSentry = Entry(root)
tolSentry.grid(row = 2,column = 1)
tolSentry.insert(0,'1.0')
# 按钮的执行函数
Button(root,text='ReDraw',command=drawNewTree).grid(row=1,column = 2,rowspan=3)
chkBtnVar = IntVar()
chkBtn = Checkbutton(root,text='Model Tree',variable=chkBtnVar)
chkBtn.grid(row=3,column = 0,columnspan=2)
# 加载数据
reDraw.rawDat = mat(loadDataSet("sine.txt"))
reDraw.testDat = arange(min(reDraw.rawDat[:,0]),max(reDraw.rawDat[:,0]),0.01)
# 设置画布大小
reDraw.f = Figure(figsize=(5,4),dpi = 100)
reDraw.canvas = FigureCanvasTkAgg(reDraw.f,master=root)
reDraw.canvas.draw()
reDraw.canvas.get_tk_widget().grid(row = 0,columnspan = 3)
# 画出拟合的直线图像
reDraw(1.0,10)
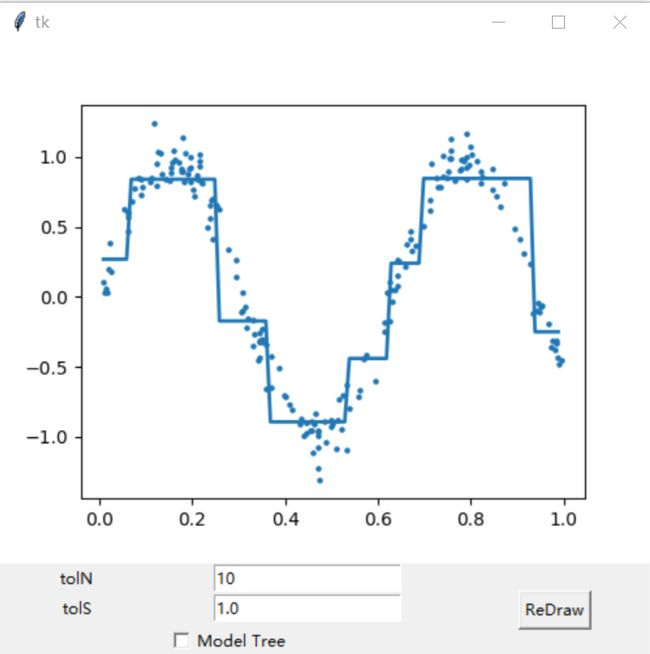
root.mainloop()得到的输出结果为:
更改tolN和tolS的值,并且根据是否选择构建模型树,可以得到不同的回归图像
8 本章小结
数据集中经常包含一些复杂的相互关系,使得输入数据和目标变量之间呈现非线性关系。对于这些复杂的关系建模,一种可行的方式时使用树来预测值分段,包括分段常数或分段直线。一般采用树结构来对这种数据建模。相应的,若叶结点使用的模型是分段常数则称为回归树,若叶节点使用的模型是线性回归方程则称为模型树。