【论文阅读笔记】 Deep Few-Shot Learning for Hyperspectral Image Classification

Deep Few-Shot Learning for Hyperspectral Image Classification

作者：Bing Liu , Xuchu Yu, Anzhu Yu, Pengqiang Zhang, Gang Wan, and Ruirui Wang

一、摘要与贡献

目前，深度学习方法已被成功用于高光谱图像（HSI）分类。然而，想要训练一个深度学习的分类器需要成千上百个标记样本。这篇文章提出了一种深度学习方法来解决HSI分类的小样本问题。在所提出的算法中有三个新颖的策略：

• 通过深度3-D残差卷积神经网络提取光谱空间特征，以降低标签的不确定性。
• 通过episodes训练网络以学习度量空间，其中来自同一类的样本距离近，来自不同类的样本距离远。
• 测试样本由学习度量空间中的最近邻居分类器分类。

这个算法的关键思想是设计的网络从训练数据集中学习度量空间。此外，这种度量空间可以推广到测试数据集的类。

这篇文章主要有以下三点贡献：

• 提出了一种DFSL(Deep Few-shot Learing)方法来训练网络以学习度量空间，该度量空间使得同一类的样本距离近。 重要的是，这样的度量空间对于训练期间未见的类别也会这样做。 因此，测试数据集的分类可以由最近邻分类器完成。
• 深度3-D卷积神经网络用于参数化度量空间。 此外，引入残差学习以更好地训练网络。 这种深度3-D残差卷积神经网络可以直接从数据立方体中提取光谱空间特征，而不依赖于任何预处理。
• 在四个已知的HSI数据集上进行了实验，证明了所提出的方法可以胜过仅有少量标记样本的传统半监督方法。

二、方法

DFSL(Deep Few-shot Learing)

图1 DFSL方法的可视化表示

随机选择来自训练集的类的子集，形成用于计算梯度和更新网络的episodes。
如图1所示，选择每个类内的样本子集作为支持集，并将剩余的的子集保留为查询集。 在本文中，每类只选择一个样本作为支持集来模拟测试数据集中小样本分类的情况。 支持集和查询集的样本通过网络馈送以提取嵌入特征。 基于嵌入空间中支持集的样本的距离的softmax计算，计算查询样本的类的分布。

具体算法如图2所示： 图2 DFSL算法步骤

Deep 3-D CNN

图3 Deep 3-D CNN的网络构架图

如图3所示，设计了具有2个残差块, 2个 池化层, 和1个卷积的网络层作为嵌入函数。 其中，虚线框是残差块。池化层将导致不同尺寸的快捷方式和主要路径。因此，在残余块中不使用池化层。相反，每个残余块与3-D最大池化层连接以减少计算和聚合特征。由于输入的高光谱数据的立方体尺寸，沿光谱维度的步幅设置为4，沿空间维度的步幅设置为2。最后，特征图可以被展开成1-D向量。图3所示的网络可以学习一个度量空间，在这个度量空间中具有相同类别的样本彼此接近。

Classification With the Nearest Neighbor

图4 在测试集上的分类流程

测试数据集的分类主要包括三个步骤：

• 通过预训练的深度残差3-D CNN提取嵌入特征;
• 计算标记样本和待分类样本之间的欧几里德距离;
• 通过NN分类器确定最终标签。

事实上，设计的深度残差3-D CNN可以被认为是训练后的嵌入功能。在测试数据集的分类过程中，所有样本通过预训练的深度残差3-D CNN提取特征。然后，随机选择一些标记的样本作为监督样本。经过训练的网络使得类似的样本在嵌入空间中彼此靠近。因此，可以通过简单的NN分析对测试样本进行分类，如图5所示。重要的是要注意训练数据集和测试数据集是彼此独立的。最后，由测试样本的标签产生的分类图与真实图匹配，以评估不同的分类方法。

图5 测试数据集中的分类（每类标记为5个样本）

三、实验和数据分析

实验数据集

（1）训练数据集
为了训练Deep 3-D CNN，收集了四个公开可用的HSI数据集。表1中列出了四个数据集的详细信息。

表1 训练数据集的详细信息

（2）测试数据集
为了证明所提方法的分类能力，对四个著名的HSI数据集进行了实验。表2列出了四种测试数据集的详细信息。

表2 测试数据集的详细信息

UP和PC数据集的前100个波段用于确保相同的输入维度。 类似地，IP和Salinas数据集的前200个频带用于分类。 在IP和Salinas数据集的测试中，前100个频带和最后100个频带通过预训练的D-Res-3D CNN来提取特征。 然后连接从前100个波段和最后100个波段中提取的特征，形成一个新的特征向量，用作分类的最终特征。

实验设置

（1）不同网络构架

表3 不同神经网络架构的总体准确度

表3中显示了四种测试数据集上，不同神经网络架构的总体准确度。在所有情况下，随着参数数量的增加，网络架构复杂性也会增加。从表3可以看出，分类精度随着网络复杂度的增加而增加，这证明了网络深度的重要性。此外，残差学习的引入也可以提高分类性能。
（2）不同卷积核的大小

表4 具有不同数量的卷积核的网络架构的总体准确度

表4中列出了具有不同数量的卷积核的网络架构的总体准确度。观察到少量卷积核（例如，2,4）大大降低了分类精度，而大量卷积核（例如，32）也将降低分类精度。将内核数设置为8或16是合适的。此外，大量卷积核（例如，16）将大大增加训练时间。
（3)不同学习率

图6 不同学习率的损失函数值

可以观察到，大的学习速率（例如，0.01）导致损失函数值明显地波动，这可能导致网络的分离。 相反，小的学习速率（例如，0.001）可以完全降低损失函数值。 因此，学习率设定为0.001。
（4）不同查询样本数

图7 UP数据集的每个类的不同查询样本数的总体准确度（％）和训练时间（以分钟为单位）（10次运行的平均值）

以UP数据集为例，每个类的不同查询样本数的总体准确度和训练时间如图7所示。查询数据集的数量分别设置为4,9,14,19,24和29。可以训练观察到，时间随查询数据集的数量线性增加。然而，随着查询数据集数量的增加，准确率很快就会饱和。因此，设定查询数据集的数量设置为19，就可以获得所期望的结果。

与半监督的方法进行比较

作者在四个数据集上对半监督方法和所提出的方法进行了比较，实验结果如表5-8所示。

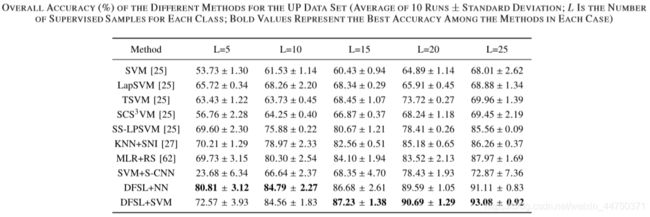
表5 在UP数据集上的准确率

表6 在PC数据集上的准确率

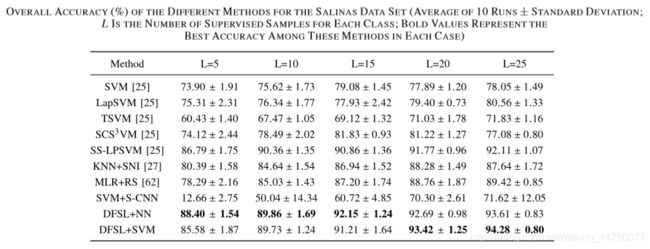
表7 在SALINAS数据集上的准确率

表8 在IP数据集上的准确率
通过上述实验可以得到以下结论：
1）分类方法的总体准确性通常随着L的增加而增加。
2）半监督方法（LapSVM，TSVM，SCS3VM和SS-LPSVM）通常优于标准SVM。
3）SVM + S-CNN表现非常差，几乎没有监督样本。
4）提出的具有NN分类器（DFSL + NN）和SVM分类器（DFSL + SVM）的DFSL方法都优于其他方法。 特别是，对于每类5个标记样本的小样本，DFSL + NN实现了优异的分类性能。

与基于CNN的方法比较

作者在四个测试数据集上对几种基于CNN的方法与所提出的方法进行比较，以进一步证明所提出方法的性能。实验结果如表10-13所示。
表9 在UP数据集上的准确率

表10 在PC数据集上的准确率

表11 在IP数据集上的准确率

表12 在SALINAS数据集上的准确率
观察可以发现，首先，D-Res-3-D CNN可以胜过CNN 和R-PCA-CNN ，证明了D-Res-3-D CNN的有效性。 此外，我们可以看到，与最先进的基于CNN的方法相比，DFSL + NN和DFSL + SVM可以提供有竞争力的结果。 这表明，当标记的样本相对足够时，所提出的方法也可以获得比较好的结果。 特别是，DFSL + SVM在UP，IP和Salinas数据集中具有最佳性能。 这表明在足够标记的样本的情况下，DFSL + SVM可以比DFSL + NN获得更好的结果。

四、总结

这篇文章提出了DFSL方法，它提供了一种解决小样本HSI分类的新方法。关键的思路是DFSL方法训练网络（文中的深度残差3-D CNN）来学习度量空间，其中来自同一类的样本接近，而来自不同类的样本按距离分开。在这样的空间中，分类可以通过简单的分类器（例如，NN）来进行。对四种广泛使用的HSI数据集进行了实验，结果证明了训练模型的泛化能力。