论文笔记: 分类不确定性计算的证据深度学习方法
摘要: 本文描述对论文 Murat Sensoy, Lance Kaplan, Melih Kandemir, Evidential deep learning to quantify classification uncertainty, NIPS 2018 的理解.
1. 动机
一个 K K K 分类问题, 并不能保证新样本属于其中某个分类. 因此, 我们既要判断它属于哪个类别, 又要知道不确定性.
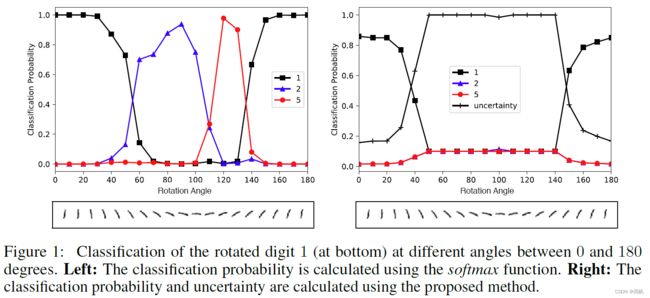
图 1. 同时计算一个字符为 1, 2, 5 的概率, 以及不确定性的概率. 当数字 1 被旋转到 6 0 ∘ − 14 0 ∘ 60^\circ-140^\circ 60∘−140∘ 时, 不确定很高.
2. 计算方法
令网络对样本的预测向量为 e = ⟨ e 1 , e 2 , … , e K ⟩ \mathbf{e} = \langle e_1, e_2, \dots, e_K \rangle e=⟨e1,e2,…,eK⟩.
又令
S = ∑ i = 1 K ( e i + 1 ) = K + ∑ i = 1 K e i (1) S = \sum_{i = 1}^K (e_i + 1) = K + \sum_{i = 1}^K e_i \tag{1} S=i=1∑K(ei+1)=K+i=1∑Kei(1)
b k = e k S (2) b_k = \frac{e_k}{S} \tag{2} bk=Sek(2) 解释为样本为第 k k k 类的概率;
u = K S (3) u = \frac{K}{S} \tag{3} u=SK(3) 解释为样本不确定的概率 (或称样本的不确定性).
注意: 分母的 S S S 的设计是为了满足
u + ∑ i = 1 K b k = 1 (4) u + \sum_{i = 1}^K b_k = 1 \tag{4} u+i=1∑Kbk=1(4)
u = k ∑ i = 1 k ( r i + 1 ) u=\frac{k}{\sum_{i=1}^k(r_i+1)} u=∑i=1k(ri+1)k,当所有 r i = 0 r_i=0 ri=0时,有 u = k / k = 1 u=k/k=1 u=k/k=1
表 1. 算例, 其中 K = 3 K = 3 K=3
| No. | e \mathbf{e} e | S S S | b \mathbf{b} b | u u u |
|---|---|---|---|---|
| 1 | ⟨ 1 , 0 , 0 ⟩ \langle 1, 0, 0 \rangle ⟨1,0,0⟩ | 4 4 4 | ⟨ 1 4 , 0 , 0 ⟩ \langle \frac{1}{4}, 0, 0 \rangle ⟨41,0,0⟩ | 3 4 \frac{3}{4} 43 |
| 2 | ⟨ 1 3 , 1 3 , 1 3 ⟩ \langle\frac{1}{3}, \frac{1}{3}, \frac{1}{3} \rangle ⟨31,31,31⟩ | 4 4 4 | ⟨ 1 12 , 1 12 , 1 12 ⟩ \langle \frac{1}{12}, \frac{1}{12}, \frac{1}{12} \rangle ⟨121,121,121⟩ | 3 4 \frac{3}{4} 43 |
| 3 | ⟨ 0 , 0 , 0 ⟩ \langle0, 0, 0 \rangle ⟨0,0,0⟩ | 3 3 3 | ⟨ 0 , 0 , 0 ⟩ \langle 0, 0, 0 \rangle ⟨0,0,0⟩ | 1 1 1 |
| 4 | ⟨ 9 , 9 , 9 ⟩ \langle9, 9, 9 \rangle ⟨9,9,9⟩ | 30 30 30 | ⟨ 9 30 , 9 30 , 9 30 ⟩ \langle \frac{9}{30}, \frac{9}{30}, \frac{9}{30} \rangle ⟨309,309,309⟩ | 3 30 \frac{3}{30} 303 |
注意:
- 如 1 号与 2 号算例所示,当预测向量的分量之和为 1 (例如经过了 softmax), 则 S ≡ K + 1 S \equiv K + 1 S≡K+1. 这不是作者的本意. 因此, 应该没有 softmax 层. 作者也提到了 softmax 层的缺点. 实际上, 网络预测的结果经过了 ReLU 层, 即向量 e \mathbf{e} e 的分量均不小于 0.
- 如 3 号算例所示, 当预测向量的分量均为 1 时, 不确定性达到最大值, 即 u = 1 u = 1 u=1.
- 如 4 号算例所示, 当预测向量的分量均较大时, 不确定性较小. 按理说这时候的不确定性应该是比较大的, 直观看应该与算例 2 是同理的 (3 个类别的预测值相同且不为 0).
疑问:
- 训练网络时, 损失是根据什么计算的? e \mathbf{e} e 还是 b ∥ u \mathbf{b} \| u b∥u? 双竖线表示连接操作.
- 如果是根据 e \mathbf{e} e, 由于标签是 ⟨ 0 , 1 , 0 ⟩ \langle 0, 1, 0 \rangle ⟨0,1,0⟩ 这种向量, 导致 e \mathbf{e} e 的分量绝对值都比较小, 容易出现算例 1, 2 所面临的问题, 即 u ≈ 3 4 u \approx \frac{3}{4} u≈43.
- 如果是根据 b ∥ u \mathbf{b} \| u b∥u, 监督信息写成 K + 1 K + 1 K+1 维向量不合理.
回答:
- 应该是在计算 e \mathbf{e} e 之前使用了 softmax 层, 输出一个分量和为 1 的向量. 这和平时网络一致. 由于训练数据的标签都不是未知类型, 因此是有道理的.
3. 例子
假设 α i = ⟨ α i 1 , … , α i K ⟩ \mathbf{\alpha}_i = \langle \alpha_{i1}, \dots, \alpha_{iK} \rangle αi=⟨αi1,…,αiK⟩ 为将 x i \mathbf{x}_i xi 进行分类的一个 Dirichlet 分布的参数. (吐槽: 使用一系列样本获得 K K K 个参数很正常, 但使用一个样本获得 K K K 个参数就很奇怪了.)
两个例子. 对于一个 3 分类问题.
- 当信任质量为 b = ⟨ 0 , 0 , 0 ⟩ \mathbf{b} = \langle 0, 0, 0 \rangle b=⟨0,0,0⟩ 时, 先验分布为 D ( p ∣ ⟨ 1 , 1 , 1 ⟩ ) D(\mathbf{p} \vert \langle 1, 1, 1 \rangle) D(p∣⟨1,1,1⟩). 表示均匀分布. 这时表示没有任何证据, 因此 u = 1 u = 1 u=1.
- 当信任质量为 b = ⟨ 0.8 , 0 , 0 ⟩ \mathbf{b} = \langle 0.8, 0, 0 \rangle b=⟨0.8,0,0⟩, 表示总的不确定性为 u = 0.2 u = 0.2 u=0.2, S = 3 / 0.2 = 15 S = 3/0.2 = 15 S=3/0.2=15. 因此, 从第 1 个类别获得的新证据为 15 × 0.8 = 12 15 \times 0.8 = 12 15×0.8=12. 这时, 观点将对应于 D ( p ∣ ⟨ 13 , 1 , 1 ⟩ ) D(\mathbf{p} \vert \langle 13, 1, 1\rangle) D(p∣⟨13,1,1⟩).
给定一个观点, 对于第 k k k 个单项的期望概率为
p ^ k = α k S . (2) \hat{p}_k = \frac{\alpha_k}{S}. \tag{2} p^k=Sαk.(2)
总的概率为 ⟨ 13 15 , 1 15 , 1 15 ⟩ \langle \frac{13}{15}, \frac{1}{15}, \frac{1}{15}\rangle ⟨1513,151,151⟩.
疑问:
- 先搞个分布 (参数表示统计特性, 好像有另外数据的样子), 又搞个期望概率 (还是统计特性, 又不需要其它数据了), 不就绕了一圈吗?
- 这里的 13 15 \frac{13}{15} 1513 算出来有啥用?
- 从 (2)式看来 b \mathbf{b} b 应该是计算结果 (输出), 为什么在这里又当成了输入, 又没提到贝叶斯之类.
4. 小结
只是根据式子来计算不确定性很容易, 但绕分布这个事情没弄懂.