【AI】浅谈梯度下降算法(理论篇)
前言
在求解机器学习算法的模型参数,即无约束优化问题时,梯度下降(Gradient Descent) 是最常采用的方法之一,另一种常用的方法是最小二乘法。
目前正在学习这方面相关的内容,因此简单谈谈与梯度下降法相关的内容。
梯度
在微积分里面,对多元函数的参数求 ∂∂∂ 偏导数,把求得的各个参数的偏导数以向量的形式写出来,就是梯度。
比如函数 f(x,y)f(x, y)f(x,y),分别对 xxx, yyy 求偏导数,求得的梯度向量就是 (∂f∂x, ∂f∂y)T(\frac{∂f}{∂x}, \frac{∂f}{∂y})^T(∂x∂f, ∂y∂f)T,简称 gradf(x,y)grad \quad f(x,y)gradf(x,y) 或者 ▽f(x,y)▽f(x,y)▽f(x,y)。对于在点 (x0,y0)(x_0,y_0)(x0,y0) 的具体梯度向量就是 (∂f∂x0, ∂f∂y0)T(\frac{∂f}{∂x_0}, \frac{∂f}{∂y_0})^T(∂x0∂f, ∂y0∂f)T 或者 ▽f(x0,y0)▽f(x_0,y_0)▽f(x0,y0),如果是3个参数的向量梯度,就是 (∂f∂x, ∂f∂y,∂f∂z)T(\frac{∂f}{∂x}, \frac{∂f}{∂y},\frac{∂f}{∂z})^T(∂x∂f, ∂y∂f,∂z∂f)T,以此类推。
那么这个梯度向量求出来有什么意义呢?他的意义从几何意义上讲,就是函数变化增加最快的地方。具体来说,对于函数 f(x,y)f(x,y)f(x,y),在点 (x0,y0)(x_0,y_0)(x0,y0),沿着梯度向量的方向,即 (∂f∂x0, ∂f∂y0)T(\frac{∂f}{∂x_0}, \frac{∂f}{∂y_0})^T(∂x0∂f, ∂y0∂f)T 的方向,是 f(x,y)f(x,y)f(x,y) 增加最快的地方。或者说,沿着梯度向量的方向,更加容易找到函数的最大值。反过来说,沿着梯度向量相反的方向,也就是 −(∂f∂x0, ∂f∂y0)T-(\frac{∂f}{∂x_0}, \frac{∂f}{∂y_0})^T−(∂x0∂f, ∂y0∂f)T 的方向,梯度减少最快,也就是更加容易找到函数的最小值。
梯度下降
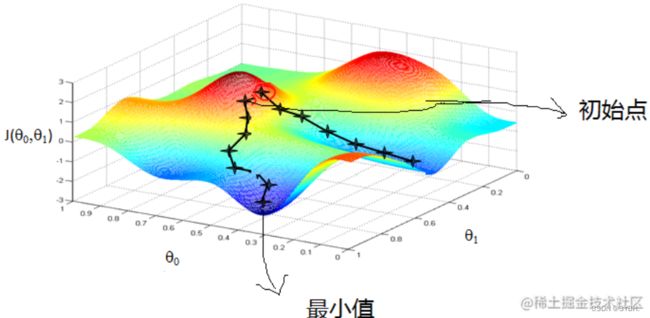
梯度下降法(英语:Gradient descent)是一个一阶最优化算法,通常也称为最陡下降法,但是不该与近似积分的最陡下降法(英语:Method of steepest descent)混淆。 要使用梯度下降法找到一个函数的局部极小值,必须向函数上当前点对应梯度(或者是近似梯度)的 反方向 的规定步长距离点进行迭代搜索。如果相反地向梯度 正方向 迭代进行搜索,则会接近函数的局部极大值点;这个过程则被称为梯度上升法。
上述对梯度下降法的描述来自于维基百科,简单概括一下就是 选取适当的初值 x0x_0x0,不断迭代更新 xxx 的值,极小化目标函数,最终收敛;
在进行算法推导时,我们还需要注意一些概念:
步长(Learning rate):步长决定了在梯度下降迭代的过程中,每一步沿梯度负方向前进的长度。特征(feature):指的是样本中输入部分,比如2个单特征的样本 (x(0),y(0))(x^{(0)},y^{(0)})(x(0),y(0)),(x(1),y(1))(x^{(1)},y^{(1)})(x(1),y(1)),则第一个样本特征为 x(0)x^{(0)}x(0),第一个样本输出为 y(0)y^{(0)}y(0)。假设函数(hypothesis function):在监督学习中,为了拟合输入样本,而使用的假设函数,记为 hθ(x)h_θ(x)hθ(x)。比如对于单个特征的 m 个样本 (x(i),y(i))(i=1,2,...,m)(x^{(i)},y^{(i)})(i=1,2,...,m)(x(i),y(i))(i=1,2,...,m),可以采用拟合函数如下: hθ(x)=θ0+θ1xh_θ(x)=θ_0+θ_1xhθ(x)=θ0+θ1x。损失函数(loss function):为了评估模型拟合的好坏,通常用损失函数来度量拟合的程度。损失函数极小化,意味着拟合程度最好,对应的模型参数即为最优参数。在线性回归中,损失函数通常为样本输出和假设函数的差取平方。 比如对于 m 个样本 (xi,yi)(i=1,2,...,m)(x_i,y_i)(i=1,2,...,m)(xi,yi)(i=1,2,...,m),采用线性回归,损失函数为:J(θ0,θ1)=∑i=1m(hθ(xi)−yi)2J(θ_0,θ_1)=∑_{i=1}^m(h_θ(x_i)−y_i)^2J(θ0,θ1)=i=1∑m(hθ(xi)−yi)2
其中 xix_ixi 表示第 iii 个样本特征,yiy_iyi 表示第 iii 个样本对应的输出,hθ(xi)h_θ(x_i)hθ(xi) 为假设函数。
算法推导
先决条件: 在线性回归的前提下,确认优化模型的假设函数和损失函数。
1、确定当前位置的损失函数的梯度,对于 θiθ_iθi,其梯度表达式如下:
∂∂θiJ(θ0,θ1...,θn)\frac{∂}{∂θ_i}J(θ_0,θ_1...,θ_n)∂θi∂J(θ0,θ1...,θn)
2、用步长 ααα (这里指机器学习中的学习率更为合适) 乘以损失函数的梯度,得到当前位置下降的距离,即
α∂∂θiJ(θ0,θ1...,θn)α\frac{∂}{∂θ_i}J(θ_0,θ_1...,θ_n)α∂θi∂J(θ0,θ1...,θn)
3、确定是否所有的 θiθ_iθi,梯度下降的距离都小于 εεε,如果小于 εεε 则算法终止,当前所有的 θi(i=0,1,...n)θ_i(i=0,1,...n)θi(i=0,1,...n) 即为最终结果,否则进入步骤4;
4、更新所有的 θθθ,对于 θiθ_iθi,其更新表达式如下,更新完毕后继续转入步骤1;
θi=θi−α∂∂θiJ(θ0,θ1...,θn)θ_i=θ_i−α\frac{∂}{∂θ_i}J(θ_0,θ_1...,θ_n)θi=θi−α∂θi∂J(θ0,θ1...,θn)
TIP
损失函数如前面先决条件所述:
J(θ0,θ1...,θn)=12m∑j=0m(hθ(x0(j),x1(j),...,xn(j))−yj)2J(θ_0,θ_1...,θ_n)=\frac{1}{2m}∑_{j=0}^m(h_θ(x^{(j)}_0,x^{(j)}_1,...,x^{(j)}_n)−y_j)^2J(θ0,θ1...,θn)=2m1j=0∑m(hθ(x0(j),x1(j),...,xn(j))−yj)2
则在算法过程步骤1中对于 θiθ_iθi 的偏导数计算如下:
∂∂θiJ(θ0,θ1...,θn)=1m∑j=0m(hθ(x0(j),x1(j),...,xn(j))−yj)xi(j)\frac{∂}{∂θ_i}J(θ_0,θ_1...,θ_n)=\frac{1}{m}∑_{j=0}^m(h_θ(x^{(j)}_0,x^{(j)}_1,...,x^{(j)}_n)−y_j)x_i^{(j)}∂θi∂J(θ0,θ1...,θn)=m1j=0∑m(hθ(x0(j),x1(j),...,xn(j))−yj)xi(j)
由于样本中没有 x0x_0x0,上式中令所有的 x0jx^j_0x0j 为1,步骤4中 θiθ_iθi 的表达式更新如下:
θi=θi−α1m∑j=0m(hθ(x0(j),x1(j),...,xn(j))−yj)xi(j)θ_i=θ_i−α\frac{1}{m}∑_{j=0}^m(h_θ(x^{(j)}_0,x^{(j)}_1,...,x^{(j)}_n)−y_j)x_i^{(j)}θi=θi−αm1j=0∑m(hθ(x0(j),x1(j),...,xn(j))−yj)xi(j)
从这个例子可以看出当前点的梯度方向是由所有的样本决定的;