基于IOU的损失函数合集, IoU, GIoU, DIoU,CIoU, EIoU
目标检测任务的损失函数一般由 Classificition Loss(分类损失函数)和Bounding Box Regeression Loss(回归损失函数)两部分构成。
Bounding Box 回归损失函数近些年的发展过程是:Smooth L1 Loss --> IoU Loss(2016)–> GIoU Loss(2019)–> DIoU Loss(2020)–> CIoU Loss(2020)–> EIoU Loss (2022)
这里从最常用的 IOU_Loss 开始,进行对比分析。
1. IoU Loss
IoU Loss 主要是通过预测框和真实框的 IoU 值来反应预测结果的好坏,如下图所示。


从上面这三个例子可以可以看出,IoU Loss 存在两个问题:
问题1: 即状态 1 的情况,当预测框和目标框不相交时,IoU=0,无法反映两个框距离的远近,此时损失函数不可导,IOU_Loss 无法优化两个框不相交的情况。
问题2: 即状态 2 和状态 3 的情况,当两个预测框大小相同,两个IOU也相同,IOU_Loss 无法区分两者相交情况的不同。
因此,2019 年出现了GIOU_Loss来进行改进。
2. GIOU Loss
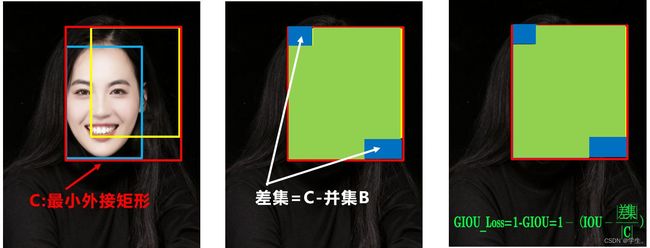
GIOU Loss 在 IOU Loss 基础上增加了相交时的衡量标准,即 |差集|/|C|, 即差集越小时说明预测框越接近真实框。但是有存在了新的问题,如下:

可以看出,上面 3 种状态差集均为 0,即 GIOU Loss 退化为 IOU Loss,GIOU Loss 也无法反映上面 3 种状态的好坏。为了解决这种问题,2020年 的 AAAI 又提出了 DIOU_Loss。
3. DIOU Loss
好的目标框回归函数应该考虑三个重要几何因素:**重叠面积、中心点距离,长宽比。**针对 IOU 和 GIOU 存在的问题,作者从两个方面进行考虑
a. 如何最小化预测框和目标框之间的归一化距离?
b. 如何在预测框和目标框重叠时,回归的更准确?
针对第一个问题,提出了 DIOU Loss(Distance_IOU_Loss)

DIOU Loss 考虑了重叠面积和中心点距离,当目标框包裹预测框的时候,直接度量 2 个框的距离,因此 DIOU Loss 收敛的更快。但就像前面好的目标框回归函数所说的,没有考虑到长宽比。

上面 3 种状态预测框和真实目标框的中心点距离是相同的,DIOU Loss 也退化成了 IOU Loss。如上面提到的目标检测回归函数需要考虑到的三种因素,DIOU Loss 没有引入长宽比的衡量。针对这个问题,CIOU Loss 被提出来。
4. CIOU Loss
CIOU Loss 和 DIOU Loss 前面的公式都是一样的,不过在此基础上还增加了一个影响因子,将预测框和目标框的长宽比都考虑进去。
CIOU_LOSS = 1 − CIOU = 1 − ( IOU − d o 2 d c 2 − v 2 1 − IOU + v ) \text{CIOU\_LOSS}=1-\text{CIOU}=1-\left( \text{IOU}-\frac{d_{\text o}^{2}}{d_{\text c}^{2}}-\frac{v^2}{1-\text{IOU}+v} \right) CIOU_LOSS=1−CIOU=1−(IOU−dc2do2−1−IOU+vv2)
其中, d o d_\text o do 为目标框和预测框的中心店欧式距离, d c d_\text c dc 为目标框的对角线距离, v v v 是衡量长宽比一致性的参数,被定义为:
v = 4 π 2 ( arctan w gt h gt − arctan w p h p ) 2 v=\frac{4}{\pi ^2}\left( \arctan \frac{w^{\text{gt}}}{h^{\text{gt}}}-\arctan \frac{w^{\text{p}}}{h^{\text{p}}} \right) ^2 v=π24(arctanhgtwgt−arctanhpwp)2
w gt , h gt w^{\text {gt}},h^{\text {gt}} wgt,hgt 是真实目标框的宽和高, w p , h p w^{\text {p}},h^{\text {p}} wp,hp 是预测框的宽高。
这样 CIOU Loss 就将目标框回归函数应该考虑三个重要几何因素:重叠面积、中心点距离,长宽比全都考虑进去了。
5. EIoU Loss 2022
论文:Focal and Efficient IOU Loss for Accurate Bounding Box Regression
动机:1. ln 损失函数和现有的基于 IoU 的损失函数都不能很好的描述 bbox ,导致模型收敛慢和不准确;2. 大多数损失函数忽略了正负样本不平衡的问题,即大量与目标框重叠面积较小的预测框在最终的 bbox 优化中占用了绝大部分的贡献。
EIOU_LOSS = L IOU + L dis + L a s p = 1 − IOU + d 2 ( b p , b gt ) ( w c ) 2 + ( h c ) 2 + d 2 ( w p , w gt ) ( w c ) 2 + d 2 ( h p , h gt ) ( h c ) 2 \text{EIOU\_LOSS}=L_{\text{IOU}}+L_{\text{dis}}+L_{asp} =1-\text{IOU}+\frac{d^2\left( \mathbf{b}^{\text{p}},\mathbf{b}^{\text{gt}} \right)}{\left( w^c \right) ^2+\left( h^c \right) ^2}+\frac{d^2\left( w^{\text{p}},w^{\text{gt}} \right)}{\left( w^c \right) ^2}+\frac{d^2\left( h^{\text{p}},h^{\text{gt}} \right)}{\left( h^c \right) ^2} EIOU_LOSS=LIOU+Ldis+Lasp=1−IOU+(wc)2+(hc)2d2(bp,bgt)+(wc)2d2(wp,wgt)+(hc)2d2(hp,hgt)
其中, b gt \mathbf{b}^{\text{gt}} bgt 和 b p \mathbf{b}^{\text{p}} bp 分别为预测框和目标框中心点的坐标, d ( b p , b gt ) d\left( \mathbf{b}^{\text{p}},\mathbf{b}^{\text{gt}} \right) d(bp,bgt) 表示两者的欧氏距离, w c , h c w^c,h^c wc,hc 是预测框和目标框最小外界矩形的宽高,与之类似, ⋆ p , ⋆ gt \star ^{\text p},\star ^{\text {gt}} ⋆p,⋆gt 分别表示预测框和目标框的相关信息, d ( w p , w gt ) d\left( w^{\text{p}},w^{\text{gt}} \right) d(wp,wgt) 表示预测框和目标框宽度的差值。
注意: [Submitted on 20 Jan 2021 (v1), last revised 16 Jul 2022 (this version, v2)]。新版本中作者用 ( w c ) 2 + ( h c ) 2 ( w^c) ^2+\left( h^c \right) ^2 (wc)2+(hc)2 替换了 v1 版本中的 c 2 c^2 c2.
回到 CIoU loss 公式中,仅看 v v v 这一项:
v = 4 π 2 ( arctan w gt h gt − arctan w p h p ) 2 v=\frac{4}{\pi ^2}\left( \arctan \frac{w^{\text{gt}}}{h^{\text{gt}}}-\arctan \frac{w^{\text{p}}}{h^{\text{p}}} \right) ^2 v=π24(arctanhgtwgt−arctanhpwp)2
可以看出,CIOU 中存在两个问题:
a. 使用的是预测框和目标框的宽高比,那当预测框的宽高满足 { ( w p = k w gt , h p = k h gt ) ∣ k ∈ R + } \{ \left( w^{\text{p}} = kw^{\text{gt}},\ h^{\text{p}} = kh^{\text{gt}} \right) | k\in \mathbb{R}^+ \} {(wp=kwgt, hp=khgt)∣k∈R+} 时,CIoU 中此项的惩罚便失去了作用。
b. 根据下面 w p , h p w^{\text p},h^{\text p} wp,hp 的梯度公式,
∂ v ∂ w p = 8 π 2 ( arctan w gt h gt − arctan w p h p ) ⋅ h p ( w p ) 2 + ( h p ) 2 \frac{\partial v}{\partial w^{\text{p}}}=\frac{8}{\pi ^2}\left( \arctan \frac{w^{\text{gt}}}{h^{\text{gt}}}-\arctan \frac{w^{\text{p}}}{h^{\text{p}}} \right) \cdot \frac{h^{\text{p}}}{\left( w^{\text{p}} \right) ^2+\left( h^{\text{p}} \right) ^2} ∂wp∂v=π28(arctanhgtwgt−arctanhpwp)⋅(wp)2+(hp)2hp
∂ v ∂ h p = − 8 π 2 ( arctan w gt h gt − arctan w p h p ) ⋅ w p ( w p ) 2 + ( h p ) 2 \frac{\partial v}{\partial h^{\text{p}}}=-\frac{8}{\pi ^2}\left( \arctan \frac{w^{\text{gt}}}{h^{\text{gt}}}-\arctan \frac{w^{\text{p}}}{h^{\text{p}}} \right) \cdot \frac{w^{\text{p}}}{\left( w^{\text{p}} \right) ^2+\left( h^{\text{p}} \right) ^2} ∂hp∂v=−π28(arctanhgtwgt−arctanhpwp)⋅(wp)2+(hp)2wp
可以得出, ∂ v ∂ w p = − h w ∂ v ∂ h p \frac{\partial v}{\partial w^{\text{p}}}=-\frac{h}{w}\frac{\partial v}{\partial h^{\text{p}}} ∂wp∂v=−wh∂hp∂v 两者的关系成反比。也就是说,训练时 w p , h p w^{\text p},h^{\text p} wp,hp 中任意一者增大时,另一者必然减小。
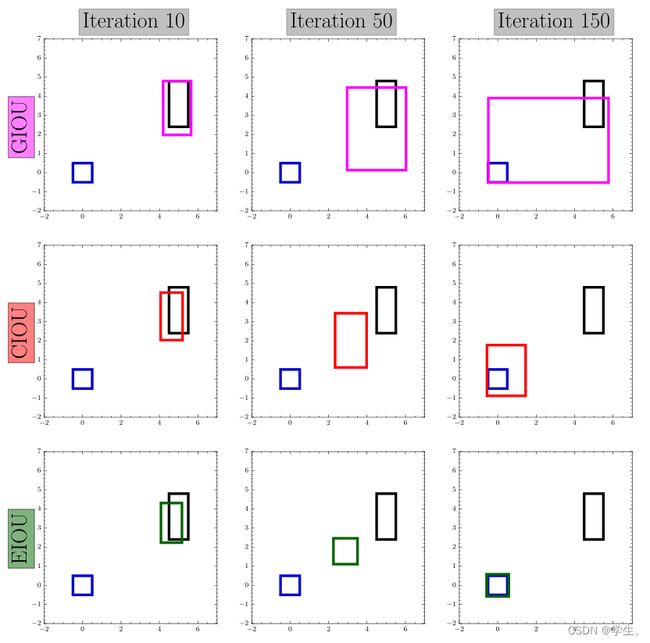
上图中,黑色框表示 anchor box,蓝色框表示目标框 ground-truth,其它三个颜色分别是对应损失函数的预测框。其中:
- GIOU 通过预测框和目标框的差集/最小外界矩形来作为惩罚项,一方面在预测框在目标框内部或目标框在预测框内部时,都无法处理比值相同的情况;另一方面,也导致 GIOU 存在先减小差集面积再优化 IoU 值的可能性。
- CIOU 存在的问题是上面提到的预测框宽高比成反比,两者不能同时增大或缩小。如上图第二行,iter=50 中预测框的宽高都大于目标框,但是在 iter=150 中,预测框的高变小,但是宽却变大。
上面提到第二个动机,目标检测模型中预测框往往数量较大,其中与目标框 IOU 值较低的低质量样本占绝大多数。低质量样本在训练时容易造成损失值波动的情况。作者认为高低质量样本分布不均是影响模型收敛的一个重要因素。作者提到,一个优秀的损失函数应该具有下面几个性质:
- 当回归的 error 是 0 的时候,此时的梯度也应当是 0,因为我们这时不再需要对参数进行调整;
- 在错误率小的地方,梯度的值也应当小,反之在错误率大的地方,梯度也应当大,因为这时候我们需要对错误率小的情况进行微调,而错误率大的地方进行大刀阔斧的调整;
- 应该有一个参数可以抑制低质量样本对损失值的影响;
- 梯度值的范围应该在一定的范围内,例如 (0,1],避免造成梯度的剧烈波动。
借助 Focal Loss 的思想,作者提出了 Focal L1 Loss,具体过程大致为:作者通过设计出一个合适的梯度函数,并根据它的性质求出相关参数的关系,通过求积分得出最终的损失函数。具体推导见论文中。作者设计的 Focal L1 Loss 的梯度函数如下:
∂ L f ∂ x = { − α x ln ( β x ) , 0 < x ≤ 1 ; 1 e ≤ β ≤ 1 − α ln ( β ) , x > 1 ; 1 e ≤ β ≤ 1 \frac{\partial \mathcal{L}_f}{\partial x}=\begin{cases} -\alpha x\ln \left( \beta x \right)& ,0
最终得出的 Focal L1 Loss 损失函数公式为:
L f ( x ) = { − α x 2 ( 2 ln ( β x ) − 1 ) 4 , 0 < x ≤ 1 ; 1 e ≤ β ≤ 1 − α ln ( β ) x + C , x > 1 ; 1 e ≤ β ≤ 1 \mathcal{L}_f\left( x \right) =\begin{cases} -\frac{\alpha x^2\left( 2\ln \left( \beta x \right) -1 \right)}{4}& ,0
其中,为了保证函数连续,令 L f ( 1 ) \mathcal{L}_f\left( 1 \right) Lf(1) 求得 C = 2 α ln β + α 4 C=\frac{2\alpha \ln \beta +\alpha}{4} C=42αlnβ+α.

上图是 FocalL1 Loss 损失函数曲线 (a) 和其梯度曲线图 (b)。从 (b) 中可以看出,FocalL1 Loss 可以通过控制 β \beta β 的大小来控制损失值超过 1 之后的梯度大小,如当 β = 1.0 \beta = 1.0 β=1.0,损失值大于 1 时,梯度值恒为 0。而且,梯度曲线呈现出上凸趋势。当损失值过大或过小时,产生的梯度值均较小。当低质量样本产生损失值较大时,此时梯度值较小,以此来抑制低质量样本的贡献。
下图与上图类似,(a)是作者期望得到的损失函数梯度曲线;(b) 是 α = 1 \alpha = 1 α=1, β \beta β 取不同值得到的损失函数图。
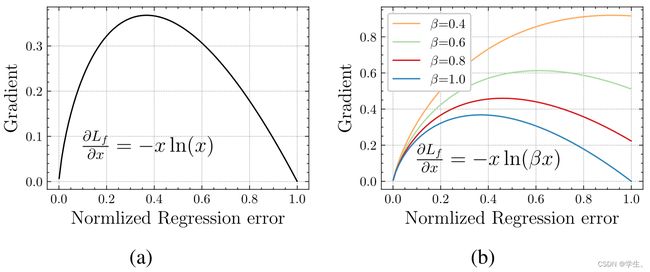
从以上两幅图中可以看出(论文中也有实验证明),当 β \beta β 越大时,低质量样本的梯度越小,即当损失值越大时,其产生梯度值越小,这里作者认为 低质量样本会产生较大的梯度。与此相反,高质量样本的梯度越大。实验发现当 β = 0.8 \beta =0.8 β=0.8 时效果最好。
在具体使用中,FocalL1 Loss 通过计算预测框和目标框 ( x , y , w , h ) (x,y,w,h) (x,y,w,h) 的位移偏差之和,来计算回归损失,如下式:
L loc = ∑ i ∈ { x , y , w , h } L f ( ∣ B i p − B i gt ∣ ) \mathcal{L}_{\text{loc}}=\sum_{i\in \left\{ x,y,w,h \right\}}{\mathcal{L}_f\left( \left| B_{i}^{\text{p}}-B_{i}^{\text{gt}} \right| \right)} Lloc=i∈{x,y,w,h}∑Lf(∣ ∣Bip−Bigt∣ ∣)
与 FocalL1 Loss 类似,作者还提出了 Focal-EIoU Loss,如下:
L Focal E − IoU = IoU γ L EIoU \mathcal{L}_{\text{Focal\,\,E}-\text{IoU}}=\text{IoU}^{\gamma}\mathcal{L}_{\text{EIoU}} LFocalE−IoU=IoUγLEIoU
Focal-EIoU Loss 提出的原因是,作者在实验中发现当 L EIoU \mathcal{L}_{\text{EIoU}} LEIoU 接近零时,它的值非常小。同时, ∂ L f ∂ L EIoU \dfrac{\partial \mathcal{L}_f}{\partial \mathcal{L}_{\text{EIoU}}} ∂LEIoU∂Lf 也非常小。当两者相乘后,会得到更小的梯度值,这会使 L EIoU \mathcal{L}_{\text{EIoU}} LEIoU 较小的高质量样本的贡献大大降低。为了解决这个问题,作者通过 IoU 值对 L EIoU \mathcal{L}_{\text{EIoU}} LEIoU 实现了权值的重置。以此来提高 L EIoU \mathcal{L}_{\text{EIoU}} LEIoU 较小的高质量样本的贡献。
同样是,通过实验发现较大的 γ \gamma γ 值对于困难样本(低质量样本),即 IOU 较小的样本抑制效果较大,可能会延缓收敛速度、影响最终精度。当 γ = 0.5 \gamma=0.5 γ=0.5 获得最好的效果。
再来综合的看下各个Loss函数的不同点:
- IOU_Loss: 主要考虑检测框和目标框重叠面积。
- GIOU_Loss: 在 IOU 的基础上,解决边界框不重合时的问题。
- DIOU_Loss: 在 IOU 和 GIOU 的基础上,考虑边界框中心点距离的信息。
- CIOU_Loss: 在 DIOU 的基础上,考虑预测框和目标框宽高比的尺度信息。
- EIOU_Loss: 在 IOU 基础上,引入目标框和预测框的长宽信息,解决了 CIOU 中长宽比等比例变化惩罚失效的问题。