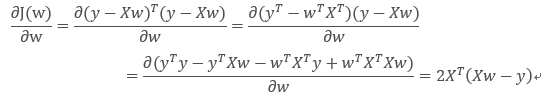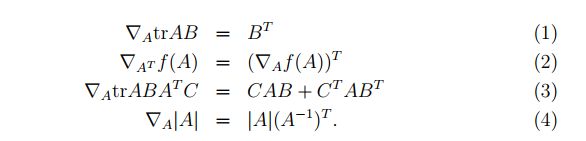我与西瓜书2----线性模型

上一章，讲了基本概念和关于模型选择与评估的概念。这一张学习线性回归，并根据线性回归加上模型选择与评估的知识来实例化。

 

1、线性回归（LinearRegression）（又名最小二乘法，ordinary least squares OLS）：基于均方误差最小化来进行模型求解的方法。
优点：线性回归没有参数，这是一个优点，但也因此无法控制模型的复杂度。另外线性模型具有很好的可解释性（comprehensibility）。

对于求解出最小二乘法所对应的参数在下面进行详细介绍一元的最小二乘法参数求解与多元相同，所以直接讲解多元线性回归参数求解）：

总的来说多元线性回归（Linear Regression with multiple variables）：

　　y=wTx+b，其中w=(w1,w2,...,wd)，

我们通过求解w和b使得f(xi)=yi，确定w和b的方法在于衡量f(x)与y之间的差别。这里我们使用的是均方误差（Mean Square Error,有时候也称为Square Loss）来度量这个差别。

通过使得MSE最小，得到参数w和b：w*=arg min(y-Xw)T(y-Xw)

这里我们令J=1/2(y-Xw)T(y-Xw)=1/2||Xw-y||²（其中 b= w0,x0=1            这里的J（w）就是代价函数（cost function）：整个训练集的函数)

注：1、我在干嘛？我在训练训练集的样本求出模型，即根据训练集样本x每个特征值来求得参数w。所以这里的x矩阵是一个n*m的矩阵，表示n个特征，训练集中有m个样本。

　　2、对于在整个训练集上的，是所有样本误差的平均，也就是损失函数的平均，称为代价函数(cost function)；

　　　  对于在单个样本上的，算的是一个样本的误差，则称为损失函数（loss function）；

            最终需要优化的函数。等于经验风险+结构风险（也就是Cost Function + 正则化项），称为目标函数（Object Function）。

　　3、对于单个样本有x=w0+w1x1+...wnxn写成矩阵的形式时候wTx是内积，即只有对角线有实数（不为零），其他位置都为0（忘记的自己在本子上内积一下就知道了）。同时对于矩阵求导就是对矩阵中的每一项求导，而对内积求导，即为对迹求导。

 

根据zTz=∑_iZ_i²，对J关于参数w求偏导并令其等于0可以求得最优参数：

注：1、这个地方∑_iZ_i²⁼zTz说明的意思是对于cost function求偏导可以写成矩阵的形式

　　2、这里的矩阵求导即对迹求导，下面是关于迹求导的几个公式（图片来自Andrew Ng Machine Learning公开课视频讲义,）：

　　

 

　　3、这里讲的很模糊，其实哪怕你拿到了这几个公式可能依然推到不出来，如果想自己推到的话，可以看上面的视频链接的68分钟的位置，有详细讲解~　

令上面的cost function为0，就得到了normal equations :。

当X^TX为满秩矩阵（full-rank matrix）或者正定矩阵（positive definite matrix）时，w=(X^TX)^-1X^Ty。

 然后我们了解一下奇异值分解X （singular value decomposition of X）

先从特征值开始。特征值分解可以得到特征值与特征向量，特征值表示的是这个特征到底有多重要，而特征向量表示这个特征是什么，可以将每一个特征向量理解为一个线性的子空间，我们可以利用这些线性的子空间干很多的事情。但是特征值分解具有局限性，变换矩阵只能是方阵，而奇异值分解是一个能适用于任意的矩阵的一种分解的方法，通过奇异值分解可以求得非满秩矩阵的伪逆。更多详细内容 参考：https://blog.csdn.net/shenziheng1/article/details/52916278

 

接着我们对线性回归进行Python实现： 

首先将pythonscikit-learn库中的一个方法：

核心方法位于scikit-learn库的linear_model中，线性回归的方法是linear_model.LinearRegression()

这个方法是使用a singular value decomposition of X（X的奇异值分解）来计算最小二乘法。所以当X矩阵的大小为(n,p)，且假设n>=p，则这个方法的时间复杂度O(np²)。

奇异值分解是对X^TX不是满秩时候，先做奇异值分解然后求伪逆的方法。

具体实现过程：

1、分类：

函数 ：train_test_split(X,y,test_size,train_size,random_state=0)

X,y 是矩阵。
test_size 应该在0 到 1 之间 ，默认为0.25。
train_size：If None, the value is automatically set to the complement of the test size.（是test_size的补集，即1-test_size）
random_state：int （取整数值）.

2、对训练集进行拟合(fit)并打印出求得的参数结果：
lr= linear_model.LinearRegression().fit(X_train,y_train)
这里“斜率”参数(w,也叫做权重或系数)被保存在coef_属性中（他是一个Numpy数组），而偏移或截距(b)保存在intercept_属性中（浮点数）：
print("lr.coef_:",lr.coef_)
print("lr.intercept_:",lr.intercept_)
注：coef_和intercept_结尾处的下划线是scikit-learn将从训练数据中得出的值保存在以下划线结尾的属性中。这样可以与用户设置的参数区分开。

3、测试训练集和测试集的性能：
print("Training set score:{:.2f}".format(lr.score(X_train,y_train)))
print("Testing set score:",lr.score(X_test,y_test))
两个的score都在0.66左右，这个值就是相关系数的平方，当这个值表示预测输出与样本输出的相关性，显然R2=1（呈现线性关系y=kx+b）效果最好，而这里R2=0.66显然这个值表明训练集和测试集效果都很差，为欠拟合。
（测试，random_state一定，则评估结果一定，为了得到平均的结果应该，使用不同的random_state）

代码：

import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn import datasets,linear_model
import matplotlib.pyplot as plt
import mglearn
################################################################################
X,y=mglearn.datasets.make_wave(n_samples=70)
j=range(1,6)
Training_score=[]
Testing_score=[]
for i in j:
    X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.25,random_state=(20*i))
    lr= linear_model.LinearRegression()
    lrf=lr.fit(X_train,y_train)
    y_predict=lr.predict(X_test)
    #print("lr.coef_:{}".format(lrf.coef_))
    #print("lr.intercept_:{:.2f}".format(lrf.intercept_))
    plt.plot(X_test,y_predict,label=i)
    Training_score.append(lrf.score(X_train,y_train))
    Testing_score.append(lrf.score(X_test,y_test))
plt.scatter(X_test,y_test)
Training_average_score=sum(Training_score)/len(Training_score)
Testing_average_score =sum(Testing_score)/len(Testing_score)
print("Training_average_score:",Training_average_score)
print("Testing_average_score:",Testing_average_score)
plt.legend()
plt.show()


    # Training_average_score: 0.6820603963437258
    # Testing_average_score: 0.5628366479885483
################################################################################

注：1、这个代码在求解参数的时候，进行了多次随机采样（因为是线性回归，不是分类不需要分层），并且去平均值作为分数结果，注重稳定性。

　　2、测试结果评估采用的是上一篇讲的R²来评估模型性能。

　　3、很显然测试结果很不好。说明这不使用与线性回归。

 

另外一种情况，当训练结果很好，测试结果很差如下（具体例子就不给出了，主要是为了引出正则化）：

Training set score:0.95

Test set score:0.61
训练集和测试集之间的性能差异是过拟合的明显标志，因此我们应该试图找到一个可以控制复杂度的模型。标准线性回归最常用的替代方法就是岭回归（ridge regression）。
下面代码分别是未使用正则化（注释掉的部分）和使用正则化的代码：

结果表明，虽然训练集的评估结果变差了，但测试集的评估分数提高了，表明通过正则化使得模型的泛化能力增强了。

import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn import datasets,linear_model
import mglearn
################################################################################
##without regularization
#
# X,y=mglearn.datasets.load_extended_boston()
# j=range(1,100)
# Training_score=[]
# Testing_score=[]
# lr=linear_model.LinearRegression()
# # print("X_test.shape :",X_test.shape,"y_predict shape:",y_predict.shape)   #X_test.shape : (127, 104) y_predict shape: (127,)
#
# for i in j:
#     X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.25,random_state=i)
#     lrf=lr.fit(X_train,y_train)
#     y_predict=lr.predict(X_test)
#     Training_score.append(lrf.score(X_train,y_train))
#     Testing_score.append(lrf.score(X_test,y_test))
# Training_average_score=sum(Training_score)/len(Training_score)
# Testing_average_score =sum(Testing_score)/len(Testing_score)
#     # print("coef_:",lrf.coef_)
# print("Training_average_score:",Training_average_score)
# print("Testing_average_score:",Testing_average_score)
#
#
# ##Training_average_score: 0.9368326849685069
# ##Testing_average_score: 0.7915812891905217
# ################################################################################
##Ridge Regression
X,y=mglearn.datasets.load_extended_boston()
j=range(0,100)
Training_score=[]
Testing_score=[]
# Ridge=linear_model.Ridge(normalize=True)#Training_average_score: 0.7854478510103376;Testing_average_score: 0.751578166025869
Ridge=linear_model.Ridge()
for i in j:
    X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.25,random_state=i)
    Ridgef=Ridge.fit(X_train,y_train)
    y_predict=Ridgef.predict(X_test)
    Training_score.append(Ridgef.score(X_train,y_train))
    Testing_score.append(Ridgef.score(X_test,y_test))
# print("coef_:",Ridgef.coef_)
Training_average_score=sum(Training_score)/len(Training_score)
Testing_average_score =sum(Testing_score)/len(Testing_score)
print("Training_average_score:",Training_average_score)
print("Testing_average_score:",Testing_average_score)
#Training_average_score: 0.8628368582406927
#Testing_average_score: 0.8224515767272093
# ################################################################################

 

转载于:https://www.cnblogs.com/SsoZhNO-1/p/9717739.html