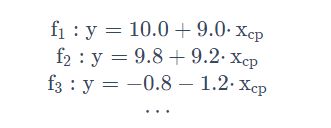DW李宏毅机器学习笔记--Task02-回归
文章目录
- 前言
- 回归定义
- 模型步骤
-
- Step 1：模型假设 - 线性模型
-
- 一元线性模型（单个特征）
- 多元线性模型（多个特征）
- Step 2：模型评估 - 损失函数
-
- 如何判断众多模型的好坏
- Step 3：最佳模型 - 梯度下降
-
- 梯度下降推演最优模型的过程
- 梯度下降算法在现实世界中面临的挑战
- w和b偏微分的计算方法
- 如何验证训练好的模型的好坏
- 更强大复杂的模型：1元N次线性模型
- 过拟合问题出现
- 步骤优化
-
- Step1优化：2个input的四个线性模型是合并到一个线性模型中
- Step2优化：如果希望模型更强大表现更好（更多参数，更多input）
- Step3优化：加入正则化
- 总结
前言
这是我在Datawhale组队学习李宏毅机器学习的记录，既作为我学习过程中的一些记录，也供同好们一起交流研究，此后还会继续更新相关内容的博客。
回归定义
回归（Regression）就是找到一个函数 ，通过输入特征值，输出一个数值 Scalar。
模型步骤
step1：模型假设，选择模型框架（线性模型）
step2：模型评估，如何判断众多模型的好坏（损失函数）
step3：模型优化，如何筛选最优的模型（梯度下降）
Step 1：模型假设 - 线性模型
一元线性模型（单个特征）
以一个特征x为例，线性模型假设为y=b+w*x。通过对b和w赋不同的值获得不同的模型。
多元线性模型（多个特征）
在实际应用中，输入特征肯定不止 x这一个，而是有多种特征。
小结：在模型假设中，应该根据已有数据的丰富度来决定是选取一元线性模型还是多元线性模型。
Step 2：模型评估 - 损失函数
【单个特征】: x 1 x^1 x1
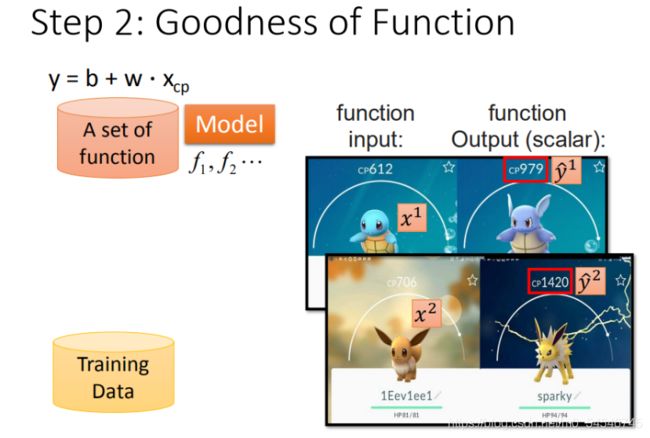
这里定义 x 1 x^1 x1 是进化前的CP值， y ^ 1 \hat{y}^1 y^1 进化后的CP值， ^ \hat{} ^ 所代表的是真实值
将10组原始数据在二维图中展示，图中的每一个点 ( x c p n , y ^ n ) (x_{cp}^n,\hat{y}^n) (xcpn,y^n) 对应着 进化前的CP值 和 进化后的CP值。
如何判断众多模型的好坏
有了这些真实的数据，那我们怎么衡量模型的好坏呢？从数学的角度来讲，我们使用距离。求【进化后的CP值】与【模型预测的CP值】差，来判定模型的好坏。也就是使用损失函数（Loss function） 来衡量模型的好坏，统计10组原始数据 ( y ^ n − f ( x c p n ) ) 2 \left ( \hat{y}^n - f(x_{cp}^n) \right )^2 (y^n−f(xcpn))2 的和，和越小模型越好。如下图所示：
上图最终简化成这种式子：
L ( f ) = ∑ n = 1 10 ( y ^ n − f ( x c p n ) ) 2 ， 将 【 f ( x ) = y 】 , 【 y = b + w ⋅ x c p 】 代 入 = ∑ n = 1 10 ( y ^ n − ( b + w ⋅ x c p ) ) 2 \begin{aligned} L(f) & = \sum_{n=1}^{10}\left ( \hat{y}^n - f(x_{cp}^n) \right )^2，将【f(x) = y】, 【y= b + w·x_{cp}】代入 \ & = \sum_{n=1}^{10}\left ( \hat{y}^n - (b + w·x_{cp}) \right )^2\ \end{aligned} L(f)=n=1∑10(y^n−f(xcpn))2，将【f(x)=y】,【y=b+w⋅xcp】代入 =n=1∑10(y^n−(b+w⋅xcp))2
最终定义 损失函数 Loss function： L ( w , b ) = ∑ n = 1 10 ( y ^ n − ( b + w ⋅ x c p ) ) 2 L(w,b)= \sum_{n=1}^{10}\left ( \hat{y}^n - (b + w·x_{cp}) \right )^2 L(w,b)=∑n=110(y^n−(b+w⋅xcp))2
我们将 w w w, b b b 在二维坐标图中展示，如图所示：
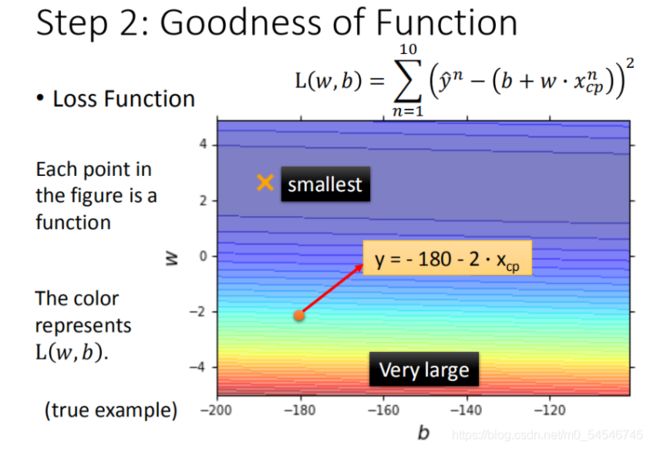
图中每一个点代表着一个模型对应的 w w w 和 b b b
颜色越深代表模型更优
可以与后面的图11（等高线）进行对比
Step 3：最佳模型 - 梯度下降
【单个特征】: x c p x_{cp} xcp
如何筛选最优的模型（参数w，b）
已知损失函数是 L ( w , b ) = ∑ n = 1 10 ( y ^ n − ( b + w ⋅ x c p ) ) 2 L(w,b)= \sum_{n=1}^{10}\left ( \hat{y}^n - (b + w·x_{cp}) \right )^2 L(w,b)=∑n=110(y^n−(b+w⋅xcp))2 ，需要找到一个令结果最小的 f ∗ f^* f∗，在实际的场景中，我们遇到的参数肯定不止 w w w, b b b。
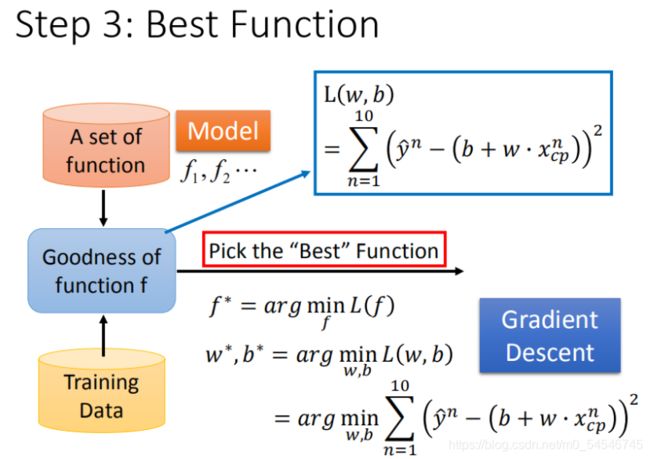
先从最简单的只有一个参数 w w w入手，定义 w ∗ = a r g min x L ( w ) w^* = arg\ \underset{x}{\operatorname{\min}} L(w) w∗=arg xminL(w)
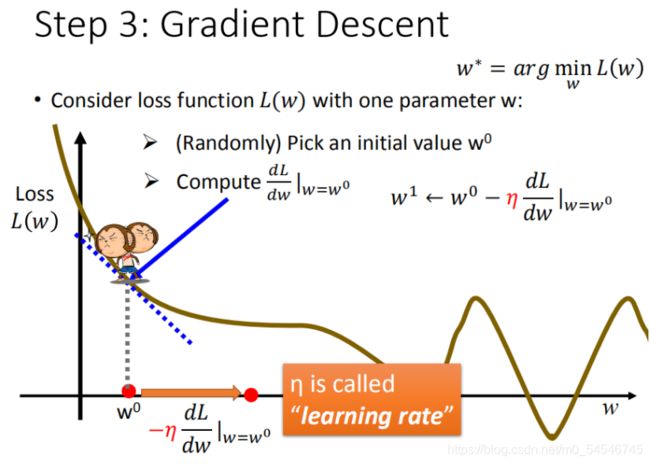
首先在这里引入一个概念 学习率 ：移动的步长，如图7中 η \eta η
- 步骤1：随机选取一个 w 0 w^0 w0
- 步骤2：计算微分，也就是当前的斜率，根据斜率来判定移动的方向
1. 大于0向右移动（增加 w w w）
2. 小于0向左移动（减少 w w w） - 步骤3：根据学习率移动
- 重复步骤2和步骤3，直到找到最低点
步骤1中，我们随机选取一个 w 0 w^0 w0，如图8所示，我们有可能会找到局部的最小值（极小值），并不是全局的最小值。
解释完单个模型参数 w w w，引入2个模型参数 w w w 和 b b b ， 其实过程是类似的，需要做的是偏微分，过程如图所示。
简而言之：
就是我们在高等数学中所学的梯度，一个由 L L L对 w w w的偏微分方程和 L L L对 b b b的偏微分方程组成的向量。
梯度下降推演最优模型的过程
如果把 w w w 和 b b b 在图形中展示：
- 每一条线围成的圈就是等高线，代表损失函数的值，颜色约深的区域代表的损失函数越小
- 红色的箭头代表等高线的法线方向
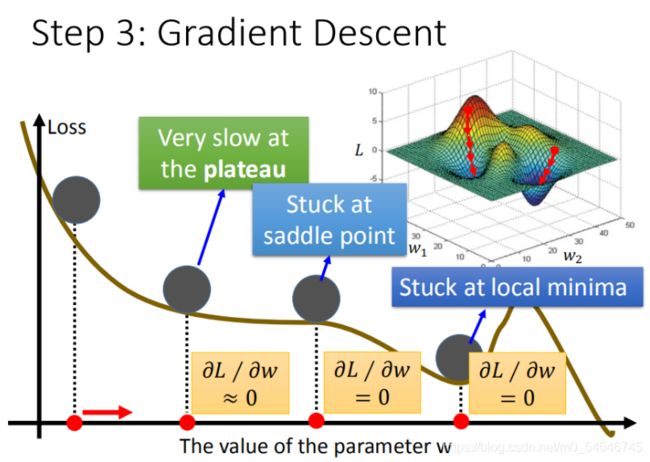
梯度下降算法在现实世界中面临的挑战
我们通过梯度下降gradient descent不断更新损失函数的结果，这个结果会越来越小，那这种方法找到的结果是否都是正确的呢？前面提到的当前最优问题外，还有没有其他存在的问题呢？
其实还会有其他的问题：
- 问题1：当前最优（Stuck at local minima）（局部最优：极小值）
- 问题2：等于0（Stuck at saddle point）（类似于三元函数在X=0时的情况）
- 问题3：趋近于0（Very slow at the plateau）（在某点的斜率为0，但在取心邻域中斜率同号大于或小于0。
w和b偏微分的计算方法
注：对b求偏导最后少了一个-1。
就是简单的求偏导。
如何验证训练好的模型的好坏
可以使用训练集和测试集的平均误差来验证模型的好坏
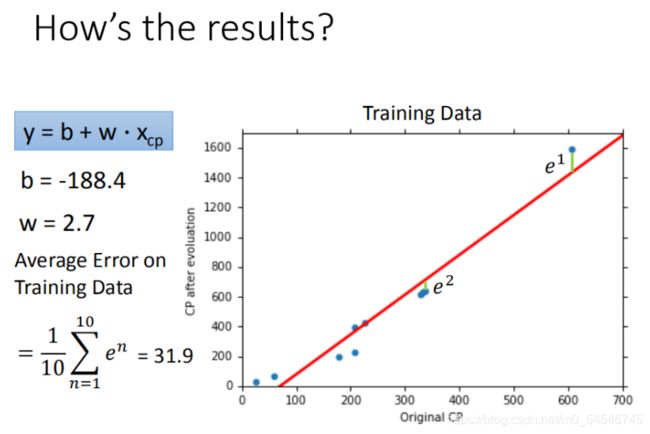
再使用10组Pokemons测试模型，测试集求得平均误差为35.0 如图所示：
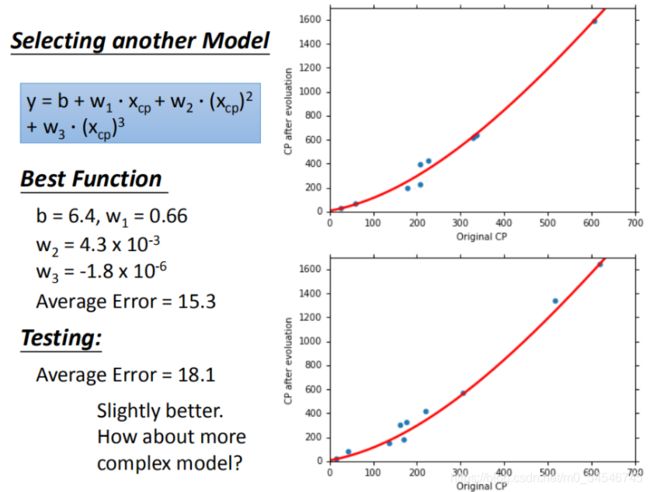
更强大复杂的模型：1元N次线性模型
在模型上，我们还可以进一部优化，选择更复杂的模型，使用1元2次方程举例，如图17，发现训练集求得平均误差为15.4，测试集的平均误差为18.4
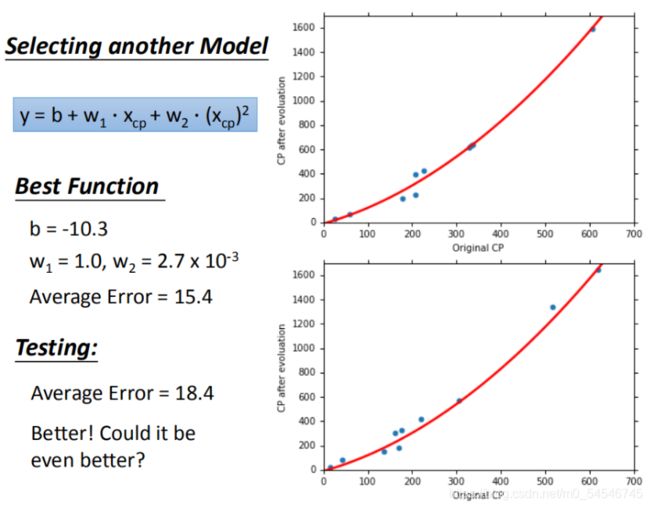
这里我们又提出一个新的问题：是不是能画出直线就是线性模型，各种复杂的曲线就是非线性模型？ 其实还是线性模型，因为把 x c p 1 x_{cp}^1 xcp1 = ( x c p ) 2 (x_{cp})^2 (xcp)2 看作一个特征，那么 y = b + w 1 ⋅ x c p + w 2 ⋅ x c p 1 y = b + w_1·x_{cp} + w_2·x_{cp}^1 y=b+w1⋅xcp+w2⋅xcp1 其实就是线性模型。
过拟合问题出现
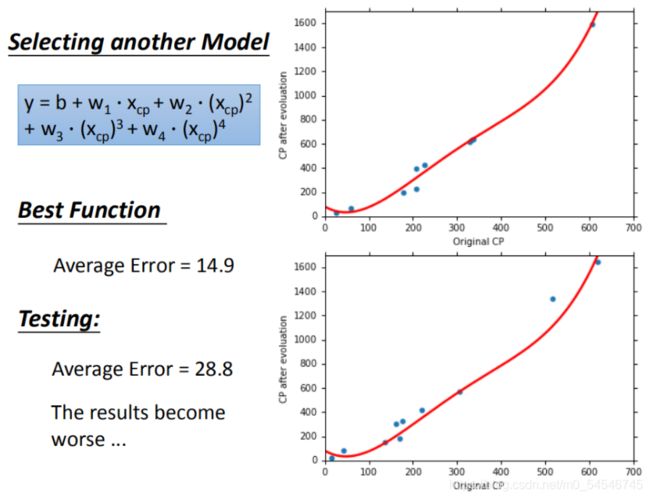
在模型上，我们再可以进一部优化，使用更高次方的模型，如图所示
- 训练集平均误差【15.4】【15.3】【14.9】【12.8】
- 测试集平均误差【18.4】【18.1】【28.8】【232.1】
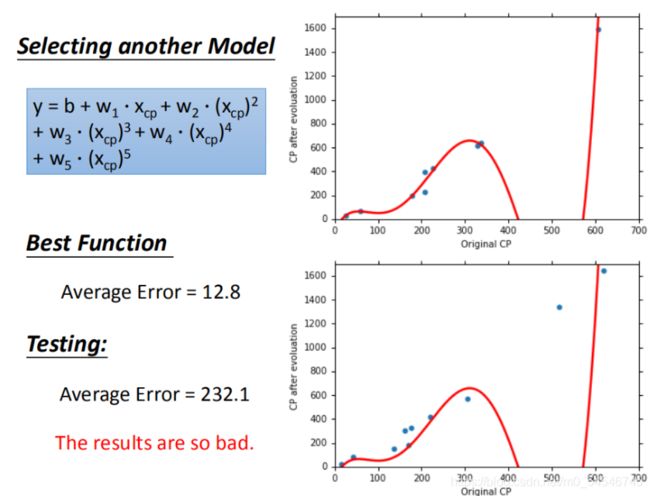
在训练集上面表现更为优秀的模型，为什么在测试集上效果反而变差了？这就是模型在训练集上过拟合的问题。
如图所示，每一个模型结果都是一个集合， 5 次 模 型 包 ⊇ 4 次 模 型 ⊇ 3 次 模 型 5次模型包 \supseteq 4次模型 \supseteq 3次模型 5次模型包⊇4次模型⊇3次模型 所以在4次模型里面找到的最佳模型，肯定不会比5次模型里面找到更差
将错误率结果图形化展示，发现3次方以上的模型，已经出现了过拟合的现象：
步骤优化
输入更多Pokemons数据，相同的起始CP值，但进化后的CP差距竟然是2倍。如图21，其实将Pokemons种类通过颜色区分，就会发现Pokemons种类是隐藏得比较深得特征，不同Pokemons种类影响了进化后的CP值的结果。
Step1优化：2个input的四个线性模型是合并到一个线性模型中
通过对 Pokemons种类 判断，将 4个线性模型 合并到一个线性模型中
Step2优化：如果希望模型更强大表现更好（更多参数，更多input）
在最开始我们有很多特征，图形化分析特征，将血量（HP）、重量（Weight）、高度（Height）也加入到模型中
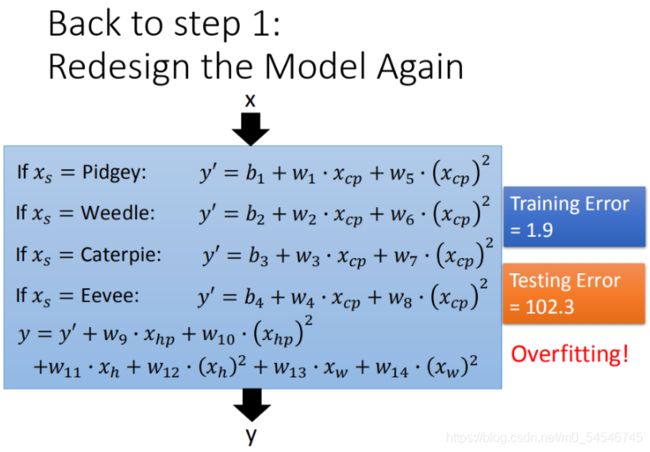
更多特征，更多input，数据量没有明显增加，仍旧导致overfitting
Step3优化：加入正则化
更多特征，但是权重 w w w 可能会使某些特征权值过高，仍旧导致overfitting，所以加入正则化
- w w w 越小，表示 f u n c t i o n function function 较平滑的， f u n c t i o n function function输出值与输入值相差不大
- 在很多应用场景中，并不是 w w w 越小模型越平滑越好，但是经验值告诉我们 w w w 越小大部分情况下都是好的。
- b b b 的值接近于0 ，对曲线平滑是没有影响
总结
- Pokemon：原始的CP值极大程度的决定了进化后的CP值，但可能还有其他的一些因素。
- Gradient descent：梯度下降的做法；后面会讲到它的理论依据和要点。
- Overfitting和Regularization：过拟合和正则化，主要介绍了表象；后面会讲到更多这方面的理论