word2vec介绍
word2vec是一种将word转为向量的方法,其包含两种算法,分别是skip-gram和CBOW,它们的最大区别是skip-gram是通过中心词去预测中心词周围的词,而CBOW是通过周围的词去预测中心词。
这个word2vec的方法是在2013年的论文《Efficient Estimation of Word Representations inVector Space》中提出的,作者来自google,文章下载链接:https://arxiv.org/pdf/1301.3781.pdf
文章提出了这两种方法如下图所示:
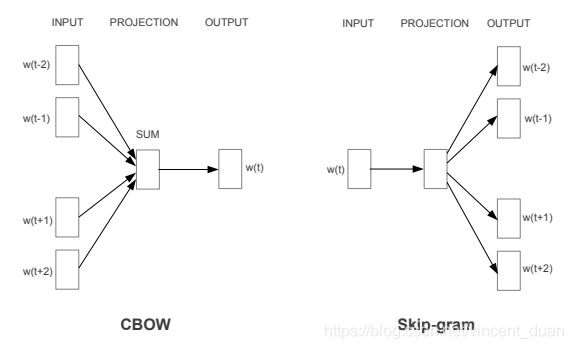
你现在看这张图可能一头雾水,不知所措,没关系,我们慢慢来学习。
在处理自然语言时,通常将词语或者字做向量化,例如one-hot编码,例如我们有一句话为:“我爱北京天安门”,我们分词后对其进行one-hot编码,结果可以是:
“我”: 【1,0,0,0】
“爱”: 【0,1,0,0】
“北京”: 【0,0,1,0】
“天安门”: 【0,0,0,1】
这样,我们就可以将每个词用一个向量表示了。
但是ont-hot编码在大量数据的情况下会出现维度灾难,通过观察我们可以知道上面的one-hot编码例子中,如果不同的词语不是4个而是n个,则one-hot编码的向量维度为1*n,也就是说,任何一个词的one-hot编码中,有一位为1,其他n-1位为0,这会导致数据非常稀疏(0特别多,1很少),存储开销也很大(n很大的情况下)。
那有什么办法可以解决这个问题呢?
于是,分布式表示被提出来了。什么是分布式表示?
它的思路是通过训练,将每个词都映射到一个较短的词向量上来。这个较短的词向量维度是多大呢?这个一般需要我们在训练时自己来指定。现在很常见的例如300维。
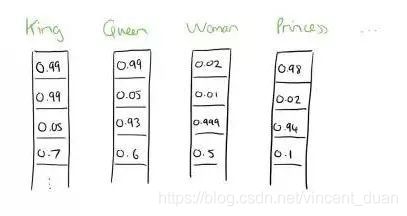
例如下面图展示了四个不同的单词,可以用一个可变化的维度长度表示(图中只画出了前4维),其实可以是多少维由你指定。假设为4维。
大家如果细心,会发现在展示的这些维度中的数字已经不是1和0了,而是一些其他的浮点数。
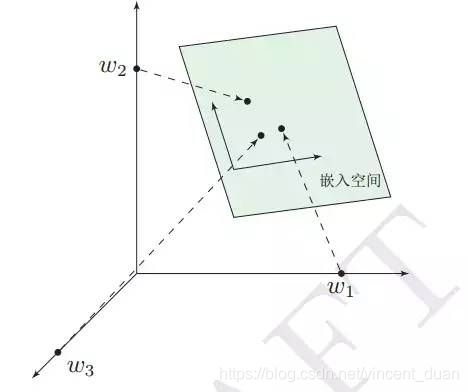
这种将高维度的词表示转换为低维度的词表示的方法,我们称之为词嵌入(word embedding)。
有个有意思的发现是,当我们使用词嵌入后,词之间可以存在一些关系,例如:
k i n g king king的词向量减去 m a n man man的词向量,再加上 w o m a n woman woman的词向量会等于 q u e e n queen queen的词向量!
![]()
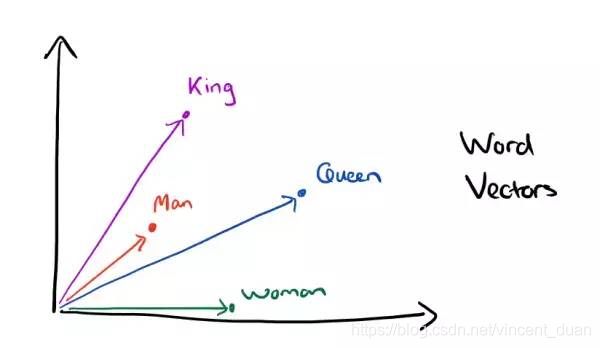
出现这种神奇现象的原因是,我们使用的分布式表示的词向量包含有词语上下文信息。
怎么理解上下文信息呢?
其实很简单,我们在上学时,做阅读理解经常会提到联系上下文,所谓的上下文信息无非是当前内容在文本中前后的其他内容信息。
如下图所示,learning这个词的上下文信息可以是它左右两边的content标记的内容。
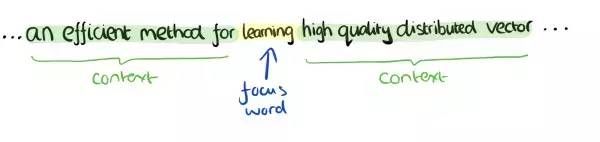
试想一下,如果这里的learning换成studying,是不是这句话仍然很合适呢?毕竟这两个单词都是学习的意思。
再转换一下思维,由于在当前上下文信息中,learning和studying都可以出现,是不是learning和studying是近义词了呢?没错,在当前的CBOW下确实是这样,甚至man和woman,cat和dog都可能是近义词。
所以大家是否理解了呢?
其实就是拥有相似或者相同的上下文的多个词可能是近义词或者同义词。
这里慢慢将CBOW的算法思想透露出来了,因为CBOW就是通过当前中心词的上下文单词信息预测当前中心词。
此时再来看CBOW这张示意图,是不是有点感觉了?
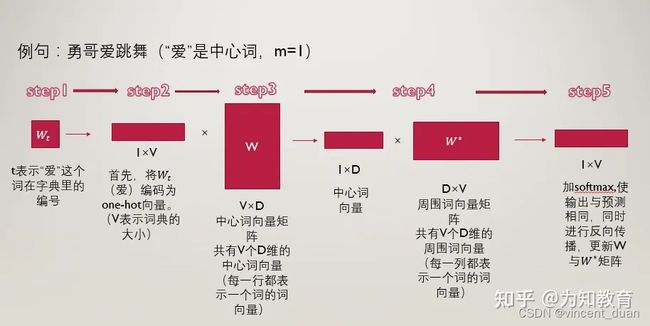
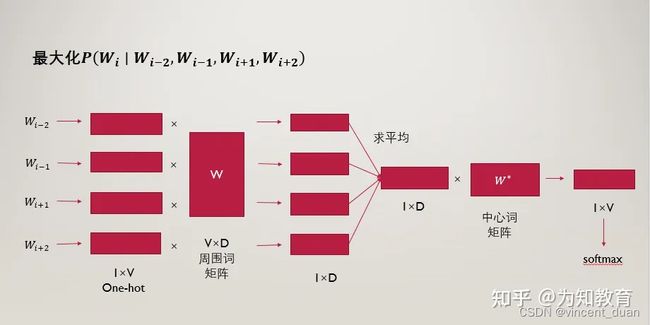
首先我们需要训练CBOW模型,该模型的结构如下图:

这张图略微复杂,我们需要从最左边开始看,最左边的一列是当前词的上下文词语,例如当前词的前两个词和后两个词,一共4个上下文词。
这些上下文词即为图中的 x 1 k x_{1k} x1k、 x 2 k x_{2k} x2k… x c k x_{ck} xck。
这些词是one-hot编码表示,维度为 1 ∗ V 1*V 1∗V(虽然图上画得像列向量 V ∗ 1 V*1 V∗1,这图画的容易理解错误,其中 V V V为词空间的大小,也就是有多少个不同的词,则one-hot编码的维度为多少,也就是 V V V个不同的词)。
然后刚说的每个上下文的词向量都需要乘以一个共享的矩阵 W W W(也可以称为周围词向量矩阵),由于整个模型是一个神经网络结构,我们将这个存在于输入层和隐藏层之间的矩阵称为 W 1 W_1 W1,该矩阵的维度为 V ∗ N V*N V∗N,其中 V V V如前所述, N N N为我们自己定义的一个维度。
学过线性代数的矩阵乘法我们知道,这里的one-hot编码向量 1 ∗ V 1*V 1∗V乘上维度为 V ∗ N V*N V∗N的矩阵 W 1 W_1 W1,结果是 1 ∗ N 1*N 1∗N的向量。
这里因为一个中心词会有多个上下文词,而每个上下文词都会计算得到一个 1 ∗ N 1*N 1∗N向量,我们将这些上下文词的 1 ∗ N 1*N 1∗N向量相加取平均,得到中间层(隐藏层)的向量,这个向量也为 1 ∗ N 1*N 1∗N,之后,这个向量需要乘以一个 N ∗ V N*V N∗V的矩阵 W 2 W_2 W2(这个向量称为中心词向量矩阵),最终得到的输出层维度为 1 ∗ V 1*V 1∗V。
然后将 1 ∗ V 1*V 1∗V的向量softmax归一化处理得到新的 1 ∗ V 1*V 1∗V向量,在 V V V个取值中概率值最大的数字对应的位置所表示的词就是预测结果。如果对softmax的概念陌生,可以搜索学习一下。
而这个输出的结果 1 ∗ V 1*V 1∗V就是预测出的中心词的分布式表示。
别急,我们只是讲通了这个CBOW模型的前向计算过程。
我们接下来说说模型的训练过程。
- 当前词的上下文词语的one-hot编码输入到输入层。
- 这些词分别乘以同一个矩阵 W 1 W_1 W1(周围词向量矩阵)后分别得到各自的 1 ∗ N 1*N 1∗N向量。
- 将这些 1 ∗ N 1*N 1∗N向量取平均为一个 1 ∗ N 1*N 1∗N向量。
- 将这个 1 ∗ N 1*N 1∗N向量乘矩阵 W 2 W_2 W2,变成一个 1 ∗ V 1*V 1∗V向量。
- 将 1 ∗ V 1*V 1∗V向量softmax归一化后输出取每个词的概率向量 1 ∗ V 1*V 1∗V。
- 将概率值最大的数对应的词作为预测词。
- 将预测的结果 1 ∗ V 1*V 1∗V向量和真实标签 1 ∗ V 1*V 1∗V向量(真实标签中的V个值中有一个是1,其他是0)计算误差,一般是交叉熵。
- 在每次前向传播之后反向传播误差,不断调整 W 1 W_1 W1和 W 2 W_2 W2矩阵的值。
预测的时候,做一次前向传播即可得到预测的中心词结果。
你可能会想,word2vec不是要将词转为分布式表示的词嵌入么?怎么变成预测中心词了?
其实我们在做CBOW时,最终要的是 W 1 W_1 W1这个 V ∗ N V*N V∗N矩阵,想想这是为什么呢?
因为我们是要将词转换为分布式表示的词嵌入,我们先将词进行one-hot编码,每个词的向量表示是 1 ∗ V 1*V 1∗V的,经过乘以 W 1 W_1 W1后,根据矩阵乘法的理解,假设 1 ∗ V 1*V 1∗V向量中第n位是1,其他是0,则矩阵乘法结果是得到了 W 1 W_1 W1矩阵中的第n行结果,也就是将词表示为了一个 1 ∗ N 1*N 1∗N的向量,一般 N N N远小于 V V V,这也就将长度为 V V V的one-hot编码稀疏词向量表示转为了稠密的长度为 N N N的词向量表示。
如果还没啥感觉,看下面这张图帮助你理解:

所以,当我们下次要查某个词的词向量时,只需要和矩阵 W 1 W_1 W1相乘就能得到结果。常用的词向量长度有300,大家想想300是不是远小于我们词表里所有不重复词的数量呢?
上面介绍的是CBOW模型,下面介绍skip-gram模型
skip-gram模型的概念是在每一次迭代中都取一个词作为中心词汇,尝试去预测它一定范围内的上下文词汇。连续词袋模型与skip-gram模型类似,最大的不同在于,连续词袋模型假设基于某中心词在文本序列前后的背景词来生成该中心词。
例如:‘我’,‘爱’,‘红色’,‘这片’,‘土地’,窗口大小为2,就是用‘我’,‘爱’,‘这片’,‘土地’这四个背景词,来预测生成 ‘红色’ 这个中心词的条件概率,即:
P(红色|我,爱,这片,土地)
以“我爱北京天安门”为例,中心词取“爱”,步长取1,也就是周围词为“我”和“北京”。
我们接下来说说模型的训练过程。(前向传播)
- 将“爱”这个词首先表示为one-hot编码输入到输入层。
- 接下来我们构建两个参数矩阵,分别为中心词矩阵和周围词矩阵,这两个矩阵分别是 V × N V×N V×N维和 N × V N×V N×V维,其中 V V V跟介绍CBOW模型一样,表示词典的大小, N N N表示我们要构建的词向量的维度,是一个超参数,我们暂时认为其是固定的,不去管它。
以中心词矩阵为例,其为 V × N V×N V×N维的,而我们的词表里一共有 V V V个词,也就是说,该矩阵的每一行都表示一个单词的中心词向量(低维、稠密的),同理,周围词向量矩阵是 N × V N×V N×V维的,每一列表示一个单词的周围词向量表示。
- 用第二步中的得到的,“爱”的one-hot编码乘以中心词向量矩阵 W 1 W_1 W1,得到一个 1 × N 1×N 1×N维的向量,这个向量可以认为是该词的中心词向量表示。
- 用该中心词向量乘以周围词向量矩阵 W 2 W_2 W2,该步骤可以理解为对于“爱”这个词,我们分别与每一个词作内积,最终得到的 1 × V 1×V 1×V向量中的每一个元素,便是该位置的词与“爱”这个词的内积大小。
- 对于最终的得到的向量,我们再进一步的做softmax归一化,归一化之后的概率越大,表示该词与“爱”的相关性越大,现在我们的目标就是要使得:“北京”这个词的概率较大,我们如何去实现这个目标呢?那就是通过调整参数矩阵 W 1 W_1 W1和 W 2 W_2 W2,(这里就可以明白这两个矩阵其实只是辅助矩阵,我们根据损失函数,使用反向传播算法来对参数矩阵进行调节,最终实现损失函数的最小化。
- 对于“爱”这个词,我们要迭代两次,第一次是使得“我”这个词的概率尽量大,第二次使得“北京”这个词的概率尽量大。然后“爱”这个词迭代完了之后,我们再去遍历这个词表里的所有词,通过一次次的迭代,逐步降低损失函数。
提问:为什么一个词汇要用两种向量表示(中心词向量和背景词向量)?
1:数学上处理更加简单
让每个单词用两个向量表示,这两个表示是相互独立的,所以在做优化的时候,他们不会相互耦合,让数学处理更加简单。
2:实际效果更好
如果每个单词用一个向量来表示,那么中心词预测下一个词是自己本身的概率就会很大,因为我们是向量内积来定义;两个单词之间的相似性。所以用两种向量表示在通过效果上会比一种向量表示更好。
在训练结束后,对于词典中任一索引为i的词,我们都会得到两组词向量,在自然语言处理应用中,一般使用skip-gram模型的中心词向量作为词的表征向量。