Solving 3D Inverse Problems using Pre-trained 2D Diffusion Models

Solving 3D Inverse Problems using Pre-trained 2D Diffusion Models

论文链接：https://arxiv.org/abs/2211.10655

GitHub链接：https://github.com/HJ-harry （期待开源）【score-MRI作者】

摘要

扩散模型已成为具有高质量样本的新的艺术生成模型，具有模式覆盖和高灵活性等有趣的特性。它们也被证明是有效的逆问题求解器，充当分布的先验，而正演模型的信息可以在采样阶段获得。然而，由于生成过程保持在相同的高维（即，与数据维相同）空间中，由于极高的内存和计算成本，模型尚未扩展到三维逆问题。在本文中，我们将传统基于模型的迭代重建的思想与现代扩散模型相结合，这导致了一种高效的方法，用于从预训练的2D扩散模型中解决三维医学图像重建任务，如稀疏视图层析成像、有限角度层析成像、压缩传感MRI。本质上，我们建议在测试时在剩余方向上使用基于模型的先验来增强2D扩散先验，从而可以在所有维度上实现相干重建。我们的方法可以在单个GPU中运行，并建立了新的最先进技术，表明所提出的方法即使在最极端的情况下（例如2视图3D断层扫描）也可以执行高保真度和精度的重建。我们进一步发现，所提出的方法的泛化能力惊人地高，可以用于重建与训练数据集完全不同的体积。

1. 介绍

扩散模型通过学习对数密度的梯度（即$\nabla xlog{p}_{data}(x)$；得分函数）[9，32]，其用于推断以创建生成样本。众所周知，这些模型能够生成高质量的样本，很好地覆盖模式，并且对训练具有很强的鲁棒性，因为它仅相当于最小化去噪问题上的均方误差损失。特别是，众所周知，扩散模型比其他流行的生成模型更稳健[8]，例如生成对抗网络（GAN）。此外，可以使用预训练的扩散模型以无监督的方式解决逆问题[5–7，15，32]。这种战略在许多情况下都非常有效，通常在每项任务上都建立了新的最先进水平。具体而言，已经提出了在稀疏视图计算机断层扫描（SV-CT）[5，31]、压缩传感MRI（CSMRI）[6，7，31]，超分辨率[4，6，15]，修补[5，15]等方面的应用。

然而，据我们所知，迄今为止所考虑的所有方法都集中于2D成像情况。这主要是由于生成约束的高维性质。具体而言，扩散模型通过从纯噪声开始生成样本，并迭代地对数据进行去噪，直到达到干净的图像。因此，生成过程涉及保持与数据相同的维度，当试图将数据维度缩放到3D时，这是禁止的。还应注意，训练3D扩散模型相当于在数据密度之前学习3D。这在两个方面是不可取的。首先，模型需要大量数据，因此训练3D模型通常需要数千个体积，而2D模型可以用少于10个体积训练。第二，先前的方法将是不必要的复杂：当涉及到动态成像或3D成像时，利用空间/时间相关性[12，33]是标准做法。天真地将问题建模为3D将错失利用此类信息的机会。

解决3D逆问题的另一种更成熟的方法是基于模型的迭代重建（MBIR）[14，17]，其中该问题被形式化为加权最小二乘（WLS）优化问题，使用数据一致性项和正则化项构建。该领域最广为人知的正则化之一是总变化（TV）惩罚[18，28]，以其有趣的特性而闻名：边缘保持，同时施加平滑度。虽然电视的前身已经被广泛探索，但众所周知，它落后于现代机器学习实践的数据驱动的前身，因为功能过于简单，无法完全模拟图像的“外观”。

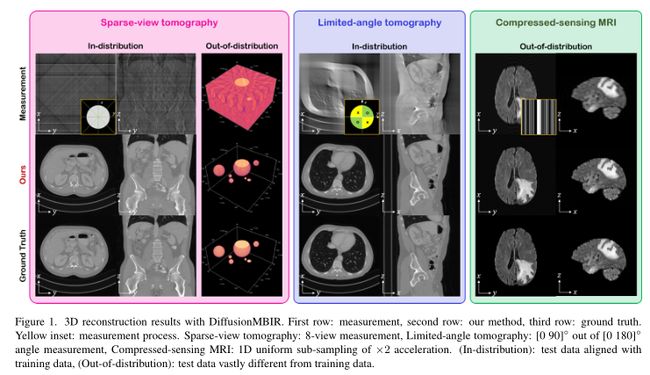
在这项工作中，我们提出了DiffusionMBIR，这是一种结合两个世界中最好的方法：我们将MBIR优化策略结合到扩散采样步骤中，以便使用仅施加到z方向的传统TV先验来增强数据驱动先验。特别地，标准反向扩散（即去噪）步骤相对于z轴独立运行，因此可以使用标准2D扩散模型。随后，通过聚集切片，然后采取交替方向乘数法（ADMM）[3]的单个更新步骤，来实施数据一致性步骤。该步骤有效地强制具有测量信息的切片与TV先验之间的串扰。为了有效优化，我们进一步提出了一种策略，我们称之为变量共享，这使我们能够在每次去噪迭代中仅使用ADMM和共轭梯度（CG）的单个扫描。注意，我们的方法是完全通用的，因为我们不限于测试时给定的前向运算符。因此，我们通过在稀疏视图CT（SV-CT）、有限角度CT（LA-CT）和压缩感测MRI（CS-MRI）上进行大量实验来验证该方法的有效性：与当前基于扩散模型的逆问题求解器相比，out方法显示出一致的改进，并在所有任务上表现出强大的性能（对于代表性结果，参见图1。关于反问题的概念说明，参见图2）。

简而言之，本文的主要贡献是设计一种基于扩散模型的重建方法，该方法1）使用体素表示进行操作，2）具有内存效率，因此我们可以将解算器缩放到更高的维度（即>256³），3）不需要数据，因此可以使用少于十个3D体积进行训练。

2. 背景

Model-based iterative reconstruction (MBIR). 考虑成像系统（如CT、MRI）的线性正向模型：
$$y=Ax+n\text{\hspace{1em}(1)}$$
其中y∈ Rm是测量值（即正弦图，kspace），$x\in {\mathbb{R}}^n$是我们希望重建的图像，$A\in {\mathbb{R}}^{m\times n}$是离散变换矩阵（即Radon，Fourier¹），n是系统中的测量噪声。由于问题是不适定的，根据测量y估计未知图像x的逆问题的标准方法是执行以下正则化重建：
$${\mathbf{x}}^{\ast }=\mathrm{argmin}\frac{1}{2}\Vert \mathbf{y}-\mathbf{A}\mathbf{x}{\Vert }_2^2+R(\mathbf{x})\text{\hspace{1em}(2)}$$
其中$R$是x的适当正则化，例如，某个变换域中的稀疏性。一个广泛使用的函数是TV惩罚，$R(x)=||Dx|{|}_{2,1}$，其中D:=[Dx，Dy，Dz]T计算每个轴上的有限差。（2）的最小化可以使用鲁棒优化算法来执行，例如快速迭代软阈值算法（FISTA）[2]或ADMM。

Score-based diffusion models. 基于分数的扩散模型是一种生成模型，它将生成过程定义为数据噪声处理的逆过程。具体地，考虑随机过程$x(t)\triangleq x_t$，t∈ [0，1]，其中我们引入时间变量t来表示随机变量的演化。特别地，我们将$p(x_0)\triangleq p_{data}(x)$（即数据分布）和$p(x_T)$定义为近似高斯分布。演化可以用以下随机微分方程形式化
$$\mathrm{d}\mathbf{x}=\mathbf{f}(\mathbf{x},t)\mathrm{d}t+g(t)\mathrm{d}\mathbf{w}\text{\hspace{1em}(3)}$$

其中$f(x,t):{\mathbb{R}}^{n\times 1}\to {\mathbb{R}}^n$是漂移函数，$g(t):\mathbb{R}\to \mathbb{R}$是标量扩散函数，$w$是n−维度标准布朗运动[27]。为了简化说明，我们表示实值变换和测量，离散傅里叶变换（DFT）矩阵和相应的测量是复值的。

$f(x,t)=0$，$g(t)=\sqrt{\frac{d\left[{\sigma }^2(t)\right]}{dt}}$。然后，SDE简化为以下布朗运动：
$$dx=\sqrt{\frac{d\left[{\sigma }^2(t)\right]}{dt}}d\mathbf{w}\text{\hspace{1em}(4)}$$
其中，平均值在整个演化过程中保持不变，而高斯噪声将被连续添加到x，随着噪声项占主导地位，最终接近纯高斯噪声。这就是文献[32]中所谓的方差分解SDE（VE-SDE），当我们在VE-SDE上构建所有方法时，我们从（4）中得出以下结果。直接应用安德森定理[1，32]可得到以下逆SDE：
$$d\mathbf{x}=-\frac{d\left[{\sigma }^2(t)\right]}{dt}{\nabla }_{{\mathbf{x}}_t}\log p\left({\mathbf{x}}_t\right)dt+\sqrt{\frac{d\left[{\sigma }^2(t)\right]}{dt}}d\overline{\mathbf{w}}\text{\hspace{1em}(5)}$$
其中$dt$, $d\overline{w}$是反向时间差，而反向标准n−维布朗运动。（5） 定义了扩散模型的生成过程，其中方程可以通过数值积分来求解。值得注意的是，积分步骤中的关键工作是分数函数$\nabla xtlogp(x_t)$，可通过去噪分数匹配（DSM）进行训练[34]
$$\underset{\theta }{\min }{\mathbb{E}}_{t,\mathbf{x}(t)}\left[\lambda (t){\Vert {\mathbf{s}}_{\theta }(\mathbf{x}(t),t)-{\nabla }_{{\mathbf{x}}_t}\log p(\mathbf{x}(t)\mid \mathbf{x}(0))\Vert }_2^2\right]\text{\hspace{1em}(6)}$$
其中$s_{\theta }(x(t),t):{\mathbb{R}}^{n\times 1}\to {\mathbb{R}}^n$是一个时间相关的神经网络，$\lambda (t)$是加权方案。自从$\nabla x_{t}logp(x(t)|x(0))$简单地是从$x(x)$中添加到$x(t)$的残余噪声，用噪声方差进行缩放，（6）的优化相当于在多个噪声尺度上训练残余去噪器，这是一种相当稳健的训练方案。虽然训练是鲁棒的，但DSM和显式得分匹配（ESM）之间的等价性可以在优化意义上建立[34]，因此$s_{\theta }^{\ast }(x(t),t)\approx \nabla x_{t}logp(x_t)$实际上可以用作插件近似值，即：
$$d\mathbf{x}\simeq -\frac{d\left[{\sigma }^2(t)\right]}{dt}{\mathbf{s}}_{{\theta }^{\ast }}(\mathbf{x}(t),t)dt+\sqrt{\frac{d\left[{\sigma }^2(t)\right]}{dt}}d\overline{\mathbf{w}}\text{\hspace{1em}(7)}$$
例如，通过将时间间隔[0，1]离散到N个区间，可以使用预测器-校正器（PC）采样器[32]来求解（7）。

3D diffusion. 由（7）明确表示的生成过程（即反向扩散）在全数据维度Rn中运行。众所周知，3D数据的体素表示很重，将数据大小缩放到64³以上需要过多的GPU内存[19]。例如，最近的一项利用扩散模型进行3D形状重建的工作[35]使用了64³大小的数据集使用扩散模型进行3D生成建模的模型通常侧重于更有效的点云表示[20，21，39]，其中点云的数量仍然少于几千（例如[20，39]中的2048×643）。自然，点云表示是有效的，但非常稀疏，当然不适合层析重建的问题，因为我们需要对内部进行精确的估计。

有一篇同时发表的研讨会论文旨在设计一种可以对3D体素表示进行建模的扩散模型[25]。在[25]中，作者通过训练潜在扩散模型[26]，训练了一个可以建模160×224×160体积的得分函数，其中潜在维度相对较小（即20×28×20）。然而，该模型需要1000个合成3D体积作为训练数据集。更重要的是，使用潜在扩散模型求解逆问题并不简单，文献中从未报道过。

Solving inverse problems with diffusion. 用近似分数函数（7）求解反向SDE相当于从先验分布$p(x)$采样。对于求解逆问题的情况，我们希望从后验分布$p(x|y)$进行采样，其中，两者之间的关系可以通过贝叶斯规则$p(x|y)=p(x)p(y|x)/p(y)$来表示，从而导致
$${\nabla }_{\mathbf{x}}\log p(\mathbf{x}\mid \mathbf{y})={\nabla }_{\mathbf{x}}\log p(\mathbf{x})+{\nabla }_{\mathbf{x}}\log p(\mathbf{y}\mid \mathbf{x})\text{\hspace{1em}(8)}$$
在这里，似然项强制数据一致性，从而诱导满足$y=Ax$的样本。文献中有两种合并（8）的方法。首先，可以将更新步骤分成1）先前的更新（即去噪），然后2）投影到测量子空间[6，32]。在离散设置中，

$$\begin{array}{rl}{\mathbf{x}}_{i-1}^{\prime }& \leftarrow \mathrm{Solve}\left({\mathbf{x}}_{i-1},{\mathbf{s}}_{{\theta }^{\ast }}\right)\end{array}\text{\hspace{1em}(9)}$$

$$\begin{array}{rl}{\mathbf{x}}_i& \leftarrow {\mathcal{P}}_{\{\mathbf{x}\mid \mathbf{A}\mathbf{x}=\mathbf{y}\}}\left({\mathbf{x}}_{i-1}^{\prime }\right)\end{array}\text{\hspace{1em}(10)}$$

其中Solve表示可以求解（7）中的逆SDE的通用数值解算器，PC表示集合C的投影算子。特别地，当使用EulerMaruyama离散化时，方程读取²。
$$\begin{array}{rl}{\mathbf{x}}_{i-1}^{\prime }& \leftarrow \left({\sigma }_i^2-{\sigma }_{i-1}^2\right){\mathbf{s}}_{{\theta }^{\ast }}\left({\mathbf{x}}_{i-1},i-1\right)+\sqrt{{\sigma }_i^2-{\sigma }_{i-1}^2}\mathbf{ϵ},\end{array}\text{\hspace{1em}(11)}$$

$$\begin{array}{rl}{\mathbf{x}}_i& \leftarrow {\mathcal{P}}_{\{\mathbf{x}\mid \mathbf{A}\mathbf{x}=\mathbf{y}\}}\left({\mathbf{x}}_{i-1}^{\prime }\right).\end{array}\text{\hspace{1em}(12)}$$

注意，Solve（·）的随机性是隐式定义的。[32]中显示，使用PC解算器，其在数值SDE解算器和蒙特卡罗-马尔可夫链（MCMC）解算器之间交替导致了优异的性能。在整个手稿中，除非另有规定，我们将PC采样器的单个步骤称为Solve（·）。或者，可以尝试显式地近似对数似然的梯度，并在单个步骤中进行更新[5]。

3. DiffusionMBIR

3.1. Main idea

为了有效地利用扩散模型进行三维重建，一种可能的解决方案是逐层应用二维扩散模型。具体地，（9）、（10）可以相对于z平行地应用−轴然而，这种方法有一个基本限制。当在不考虑切片之间的相互依赖性的情况下运行步骤时，重建的切片将彼此不相干（尤其是当我们具有更稀疏的视角时）。因此，当从冠状面/矢状面切片观察时，图像包含严重的伪影。（见图3,4（d）第2-3行）。

为了解决这个问题，我们有兴趣将MBIR和扩散模型的优点结合起来，以抑制不需要的伪影。具体而言，我们的建议是采用（9）、（10）中的交替最小化方法，但不是在二维域中应用它们，而是逐层应用（9）中基于扩散的去噪步骤，而用三维体积中的ADMM更新步骤代替（10）的二维投影步骤。具体来说，我们考虑以下子问题
$$\underset{\mathbf{x}}{\min }\frac{1}{2}\Vert \mathbf{y}-\mathbf{A}\mathbf{x}{\Vert }_2^2+{\Vert {\mathbf{D}}_z\mathbf{x}\Vert }_1\text{\hspace{1em}(13)}$$
与采用$||Dx|{|}_1$的传统TV算法不同，我们只采用z中有限差分的‘1范数−轴这种选择源于这样一个事实，即关于xy平面的先验已经由神经网络$s_{\theta }^{\ast }$, 我们需要暗示的是关于剩余方向的空间相关性。换句话说，我们用基于模型的稀疏先验来增强生成先验。从我们的实验中，我们观察到，我们的先前增强策略在产生贯穿所有三个轴的连贯3D重建方面非常有效。

3.2. Algorithmic steps

我们到达更新步骤：
$$\begin{array}{rl}{\mathbf{x}}^{+}& ={\left({\mathbf{A}}^T\mathbf{A}+\rho {\mathbf{D}}_z^T{\mathbf{D}}_z\right)}^{-1}\left({\mathbf{A}}^T\mathbf{y}+\rho {\mathbf{D}}^T(\mathbf{z}-\mathbf{w})\right)\end{array}\text{\hspace{1em}(14)}$$
$$\begin{array}{rl}{\mathbf{z}}^{+}& ={\mathcal{S}}_{\lambda /\rho }\left({\mathbf{D}}_z{\mathbf{x}}^{+}+\mathbf{w}\right)\end{array}\text{\hspace{1em}(15)}$$
$$\begin{array}{rl}{\mathbf{w}}^{+}& =\mathbf{w}+{\mathbf{D}}_z{\mathbf{x}}^{+}-{\mathbf{z}}^{+}\end{array}\text{\hspace{1em}(16)}$$
其中ρ是乘数法的超参数，S是软阈值算子。此外，（14）可以用共轭梯度（CG）求解，它有效地找到满足$Ax=b$的x的解：我们将初始点x的CG的K次迭代表示为CG（a，b，x，K）。ADMM步骤的完整推导在补充部分A中提供。为简单起见，我们将（14）、（15）、（16）的一次扫描表示为x+，z+，w+=ADMM（x，z，w）。ADMM（x，z，w）的迭代应用将稳健地解决（13）中的最小化问题。因此，所提出算法的实现将是
$$\begin{array}{rl}& {\mathbf{x}}_{i-1}^{\prime }\leftarrow \mathrm{Solve}\left({\mathbf{x}}_i,{\mathbf{s}}_{{\theta }^{\ast }}\right)\end{array}\text{\hspace{1em}(17)}$$
$$\begin{array}{rl}& {\mathbf{x}}_{i-1}\leftarrow \underset{{\mathbf{x}}_{i-1}^{\prime }}{\mathrm{argmin}}\frac{1}{2}{\Vert \mathbf{y}-\mathbf{A}{\mathbf{x}}_{i-1}^{\prime }\Vert }_2^2+{\Vert {\mathbf{D}}_z{\mathbf{x}}_{i-1}^{\prime }\Vert }_1\end{array}\text{\hspace{1em}(18)}$$
具体而言，（17）将相当于每个切片的并行去噪，而（18）增强了z方向TV先验并施加一致性。参见补充部分算法2中的详细（慢速版本）求解步骤。这里，请注意，算法中有三个迭代源：1）SDE的数值积分，以i为索引，2）ADMM迭代，以及3）内部CG迭代，用于求解（14）。由于扩散模型本身是缓慢的，因子2）、3）的乘法附加成本将是禁止性的，应该避免。在下文中，我们设计了一种简单的方法来显著降低成本。

Fast and efficient implementation (variable sharing) 在算法2中，每次在SDE的第i次迭代运行ADMM迭代之前，我们都重新初始化原始变量z和对偶变量w。反过来，这将导致ADMM算法的缓慢收敛，因为前几次迭代需要变量z，w的老化期。此外，由于求解扩散模型将有大量离散化步骤N，因此两个相邻迭代$x_i$和$x_{i+1}$之间的差异最小。当从第i+1次迭代中删除z，w的值并在第i次迭代中重新初始化时，将丢失有价值的信息，并浪费计算。因此，我们建议在SDE迭代开始之前将$z_N$和$w_N$初始化为全局变量，并始终保持更新的值。有趣的是，我们发现选择M=1，K=1，即ADMM和CG的单次迭代对于高保真重建是必要的。我们的快速版本的DiffusionMBIR在算法1中给出。

另一个警告是，在整个体积上运行神经网络正向传递是不可行的，例如，在将解算器安装到单个商品GPU中时。可以通过将批次维度3划分为子批次，分别运行子补丁的去噪步骤，然后再次将它们聚集到整个体积中来避免这种情况。ADMM步骤可以应用于聚合后的整个体积，这将产生与算法1相同的解决方案。对于算法的慢速和快速版本，当希望精确匹配测量约束时，也可以在末尾将投影应用于测量子空间。

4. Experimental setup

我们对医学图像重建中研究最广泛的三项任务进行了实验：1）稀疏视图CT（SV-CT）、2）有限角度CT（LA-CT）和3）压缩传感MRI（CS-MRI）。具体细节见补充部分B。

数据集。对于两种CT重建任务（即SV-CT、LA-CT），我们使用来自AAPM 2016 CT低剂量大挑战的数据。除一卷外的所有卷用于训练2D分数函数，一卷用于测试。对于CS-MRI任务，我们从多模态脑肿瘤图像分割基准（BRA TS）[22]2018 FLAIR体积中获取数据进行测试。注意，我们使用的是仅在fastMRI膝关节[36]图像上训练的预训练分数函数，因此我们不需要在这里分割训练/测试数据。

网络训练、推理。对于CT任务，我们在AAPM数据集上训练ncsnpp模型[32]，该数据集由约3000个2D训练数据切片组成。对于CS-MRI任务，我们采用4[7]中的预训练模型检查点。对于推理（即生成；逆问题求解），我们将采样器基于[32]的预测器-校正器（PC）采样方案。我们设置N=2000，这相当于用$s_{\theta }^{\ast }$进行4000次功能评估。

比较方法和评估。对于CT任务，我们首先将我们的方法与Chung等人[5]进行比较，这是CT重建的另一种扩散模型方法，优于[30]。由于使用[5]的流形约束梯度（MCG）需要10GB VRAM用于单个2D切片（256×256），因此我们不可能利用这种梯度步骤进行3D重建。因此，我们采用[5]的凸集投影（POCS）策略，这相当于在每个数据一致性施加步骤中采用代数重建技术（ART）。我们还与一些最好的完全监督的方法进行了比较。即，我们将Lahiri等人[16]和FBPConvNet[11]（SV-CT）/Zhang等人[37]（LA-CT）作为基线。对于[16]的实现，我们使用了两个阶段，但将去条纹CNN实现为U-Nets，而不是更简单的CNN。最后，我们包括各向同性ADMM-TV，它使用正则化函数$R(x)=||Dx|{|}_{2,1}$。

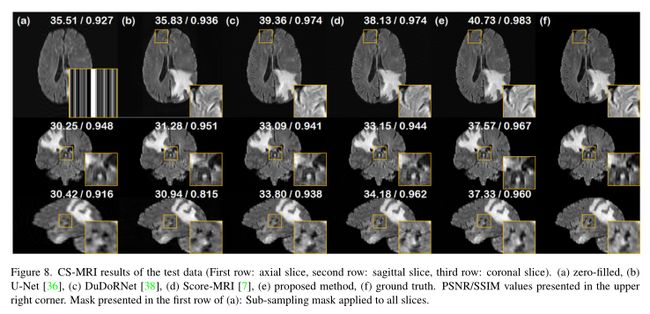
在CS-MRI实验中，我们将分数MRI[7]作为代表性的扩散模型求解器进行了比较。此外，我们还与DuDoRNet[38]和U-Net[36]进行了比较。注意，包括我们在内的所有网络，训练数据集（fastMRI膝关节）的设置故意不同于测试数据（BRA TS Flair），因为已经表明，基于扩散模型的逆问题求解器对CSMRI设置中的分布外（OOD）数据相当稳健[7，10]。定量评估采用两个标准指标：峰值信噪比（PSNR）和结构相似性指数（SSIM）。我们报告了在每个平面方向上平均的度量，因为我们期望$xy$切片与$xz$和$yz$切片相比具有不同的性能。

5. 结果

在本节中，我们将介绍所提出方法的结果。有关进一步的实验和消融研究，请参阅补充章节C。

Sparse-view CT

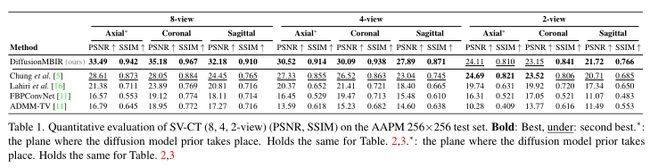
我们在表1中给出了SV-CT重建结果的定量度量。该表显示，在大多数设置中，所提出的方法以大幅度超出基线。图3和补充图6显示了8，4视图SV-CT重建结果。如每个图的第一行所示，与基线相比，所提出方法的轴向切片恢复了更精细的细节。此外，第二行和第三行的矢状和冠状切片的结果表明，DiffusionMBIR可以在所有方向上保持原始结构的结构连接性。相比之下，Chung等人[5]在重建轴向切片方面表现良好，但在z方向上没有空间完整性，导致冠状面/矢状面切片中清晰可见的粗糙伪影。Lahiri等人[16]经常忽略重要细节，无法重建，尤其是当我们只有4个视图时。由于设置极为有限，ADMM-TV很难产生令人满意的结果。

Limited angle CT

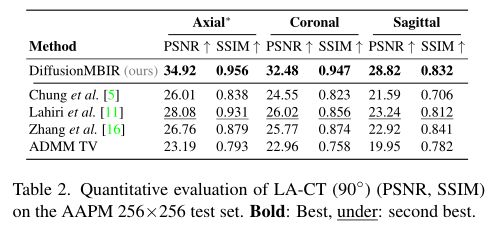
有限角度层析成像的结果如表2和图4所示。我们对[0，90]中的测量进行了测试◦ 在[90，180]中没有测量◦ 政体因此，任务是填充缺失的视图。与SV-CT实验中观察到的结果一致，我们发现DiffusionMBIR比传统的基于扩散模型的方法提高了[5]，并且也优于其他完全监督的方法，在那里我们看到提出的方法和所有其他方法性能差距甚至更大。值得注意的是，Chung等人[5]没有利用来自相邻切片的信息，因此在如何填充缺失的角度方面具有高度的自由度。由于重建是随机的，我们不能在不同切片之间施加一致性。通常，这会导致躯干结构完全扭曲，如图4（d）的第一行所示。相比之下，我们的增强先验在帧之间施加了平滑度，并且自然地稳健地保持了结构。

Compressed Sensing MRI

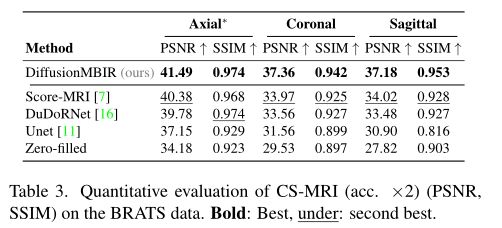
我们在一维均匀随机子采样图像的重建上测试了我们的方法，如[36]中所用。具体来说，我们将15%的自动校准信号（ACS）区域保持在中心，并且仅保留一半的k空间采样线，对应于采集方案的大约2×加速因子。结果如表3和补充图8所示。与SV-CT和LA-CT实验中观察到的结果一致，我们观察到了大量对现有技术的改进。

Out-of-distribution performance

在CS-MRI的背景下表明，扩散模型对分布外（OOD）数据具有惊人的鲁棒性[7，10]。例如，用质子密度加权冠状膝关节扫描训练的评分函数只能概括出几乎所有测试时从未见过的不同解剖结构和对比度。这种概括能力是否也适用于CT？在这里，我们用肯定的答案回答，并表明，使用所提出的方法，即使目标地面真相与训练数据集中的情况有很大不同，也可以使用相同的分数函数。

在图5中，我们显示了这种OOD重建的两种不同情况（即轻度和重度）。对于这两种情况，我们看到8视图足以产生高保真度重建，从而精确地估计地面真相。请注意，我们的先验是从人体解剖构造而来的，这与图5（b）中给出的有很大不同。直观地说，从贝叶斯角度来看，这意味着我们的扩散先验在图像上的质量很小，如图5（b）所示。尽管如此，我们可以解释，扩散模型倾向于将一些质量放置到这些严重OOD区域。因此，当结合足够的似然信息时，就足以指导正确的后验抽样，如本实验所见。这种特性在医学成像中特别有用，其中训练数据主要由正常患者数据组成，因此分布偏向于没有病理学的图像。当在测试时，我们得到包含病变的患者扫描时，我们需要一种能够在这种情况下完全概括的方法。

Choice of augmented prior

在这项工作中，我们提出用基于模型的TV先验来增强扩散生成先验，其中我们选择仅在冗余z中施加TV约束−方向，同时xy−plane完好无损。这种设计选择源于我们的假设，即扩散先验比TV先验更好地匹配实际先验分布，并且与TV先验混合可能会损害扩散先验的能力。为了验证这种情况确实存在，我们之前对TV（xyz）和TV（z）进行了消融研究。补充图10显示了先验的视觉和数值结果。这两个先验在PSNR和SSIM上得分都很高，但我们可以发现，与所提出的先验的样本相比，在xy平面上具有TV先验的图像是模糊的。分析表明，使用TV（xyz）先验使结果与训练有素的扩散先验有点不同。

6. 结论

在这项工作中，我们提出了DiffusionMBIR，这是一种基于扩散模型的重建策略，用于执行3D医学图像重建。我们表明，我们所需要的是一个2D扩散模型，该模型可以用很少的数据（<10 volumes）进行训练，并通过在冗余z方向上操作的经典电视模型进行增强。我们设计了一种方法，以有效的方式将通常的扩散模型采样步骤与ADMM迭代无缝集成。结果表明，所提出的方法能够在Sparseview CT、有限角度CT和压缩传感MRI上实现最先进的重建。特别是对于稀疏视图CT，我们表明，即使只有两个视图，我们的方法也能够提供精确的重建。最后，我们证明了DiffusionMBIR能够重建OOD数据，这与训练数据中呈现的数据有很大不同。

Supplementary Material

A. ADMM-TV

B. Details of experiment

B.1. Dataset

B.2. Details of network training

B.3. Comparison methods

C. Further experiments

C.1. Additional experimental results

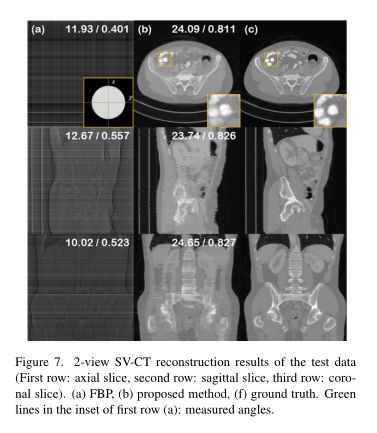
4视图稀疏视图层析重建如图6所示。此外，我们证明我们甚至可以执行2视图重建，如图7所示。在这种情况下，测量中包含的信息非常少且稀少——显然不足以实现精确的重建。然而，当我们利用生成先验时，我们可以对多个重建进行采样，这些重建1）完全可行，2）看起来很现实。尽管这在医学成像领域可能并不重要，但它可能会极大地影响需要从非常有限的采集中进行近似重建的领域。

C.2. Number of views vs. performance

我们已经验证了我们可以用所提出的方法进行极稀疏重建。人们可以自然地询问所提出的方法在测量的视图数与重建性能之间的关系的局限性和趋势，如图9所示。注意，给定的图是x轴上的对数图（即视图数）。如果我们将测量次数增加到16次以上，我们可以很容易地看到性能上限，并且我们还可以看到，减少到8次视图，我们可以在性能略有下降的情况下获得重建。当我们将视图数降至4以下时，性能开始严重下降。我们得出结论，存在一个奇点，即使我们有非常强大的重建算法，测量中的信息仍然不够。