完整的模糊推理系统介绍以及matlab中从零实现(上篇)
模糊推理系统建模
在matlab中,通过调用文档命令doc fuzzy可以得到一个模糊工具箱的完整介绍。
我也是因为工作需要,在看完师姐论文后,仍然迷迷糊糊地。相信有许多人和我一样,在网上查了一堆论文、博客,可能也没有搞得太明白。
通过几天的认真阅读文档,并从零开始实现了一个模糊推理系统后。我打算通过这个博客来整理一下自己的心得。并且希望能够帮助到和我有同样需求的同学。
模糊逻辑基础
首先,对于一个模糊推理系统,其系统框图可以表现为如下形式
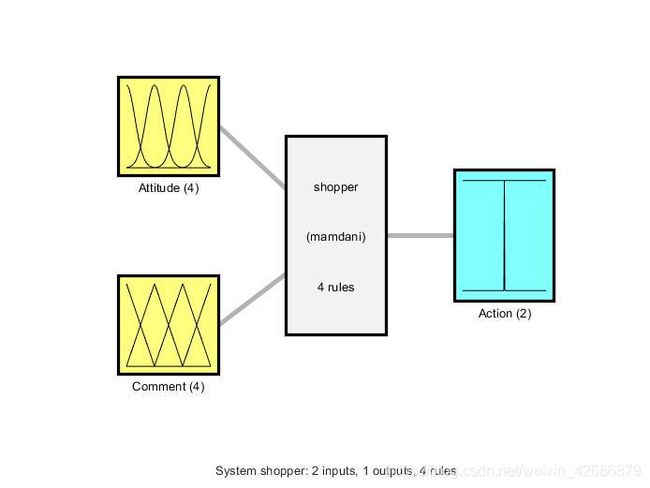
在给定输入的情况下,通过我们设定好的模糊推理系统,得到其结果输出。
此外,在开始创建自己的模糊推理系统时,需要了解认识一些相关的术语。
模糊集
摘抄文档英文解释就是:A fuzzy set is a set without a crisp, clearly defined boundary. It can contain elements with only a partial degree of membership.
相较于传统的集合,模糊集之间的界限划分更加模糊,每个元素是以[0,1]区间的数值隶属于该集合。而不是传统的属于(1)和不属于(0)。
并且,matlab中还给了一个形象生动的举例。对于周五,是否应该属于集合周末呢? 如果按照传统集合定义,它只能属于或者不属于。下图左。
而按照模糊集定义,他在一定程度上也算周末。如果我们认为这种程度比较明显,那么下图右的weekend-ness的值更加接近于1.
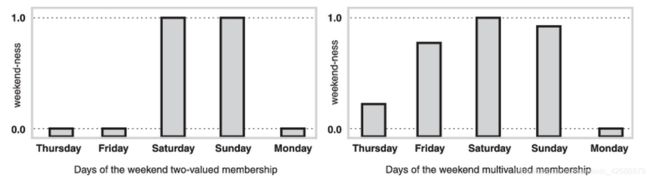
更进一步,考虑一周的每个小时,每一分是否属于周末,那么对于周五的不同时刻而言,上午属于周末的可能性更低,而晚上更容易被判定为周末。就可以得到如下更为连续的曲线图。
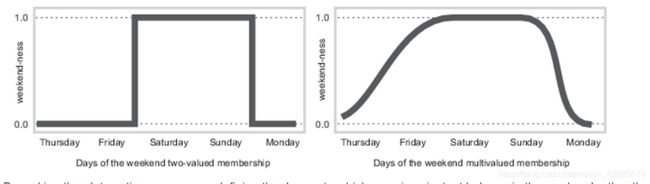
上图,也有一个专有的名字:隶属度函数或者membershipfunction,就是用来刻画输入变量属于模糊集的程度。在多大程度上符合模糊集定义。
现在对于模糊集的定义有了一个基本的认识。那么,我们可以发现生活中,存在着不少模糊集的概念。对于一个人的属性而言。高矮、胖瘦等,都是一个模糊的概念,都可以看做一个模糊集。
语义变量
在上一节中,我们了解到了什么是模糊集以及生活中的模糊集举例。现在问题来了,对于任何一个输入,它可能需要根据需要进行多层次划分。得到不同的模糊集合。那么每个模糊集合需要进行命名以免混淆。因此,语义变量就是用来标识模糊集合的。
同样以人的属性为例。我们可以做如下划分
| 属性 | 划分 |
|---|---|
| 身高 | 高、矮 |
| 身高 | 很高、高、矮、很矮 |
| 体重 | 胖、瘦 |
| … | … |
表中第二列的划分,都属于语义变量,分别代表一个模糊集合。那么,假定输入张三的身高为180cm,我们可以凭生活经验判断,张三为高的程度很大。也就是属于模糊集合高的数值越大(用[0 1]之间数值表示)。同时,为矮的可能性更小,属于模糊集合矮的数字越小。

隶属度函数
对于每一个输入,不同的划分标准可以得到不同的语义变量和多个模糊集合。然后每个语义变量也要求有一个相应的隶属度函数与之对应。用来将输入变量映射到[0 1]区间的隶属度上去。
matlab提供了许多不同的隶属度函数供大家直接调用。常用的有
- 三角隶属度函数:trimf
- 梯形隶属度函数:trapmf
- 高斯和二元高斯隶属度函数:gaussmf,gauss2mf
根据不同的需要进行选择。更多的隶属度函数以及调用格式可以参考matlab的隶属度函数介绍
当然,也可以自己创建新的隶属度函数。我有试过,但是失败了。有成功的朋友麻烦教教我
模糊推理规则,IF-THEN Rules
在我们将输入进行分类,得到语义变量并设定好隶属度函数后。对于每个不同的输入,我们均可以得到不同的隶属度值。
进一步,我们需要将这些隶属度值进行转化,根据一定的规则进行推理。
比如,我们可以设定如下规则。
如果 张三体重为胖且身高为矮 那么建议他减肥
用逻辑语言表述即为
if 张三体重== 胖&&身高 ==矮 then 建议减肥
在传统集合下,张三只能被判定为要么胖、要么瘦;要么高、要么矮。因此逻辑结果只能为0,1。其逻辑运算表为

而现在,高矮胖瘦属于一个模糊的概念。在给定身高、体重的情况下,符合每个集合的程度不再是0,1的离散值。而是[0 1]区间的连续值。因此需要将传统的逻辑运算进行拓展,在保证值仅为0,1时逻辑正确的基础上,能用于(0,1)区间的值
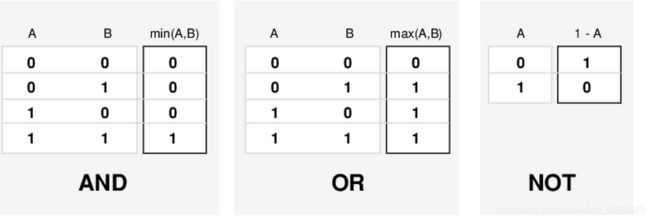
通过将AND运算等价为min,OR等价为max,NOT A等价为1-A,使得传统逻辑运算得到扩充。
那么在对张三体重进行隶属度划分以后,假如得到其隶属于胖的程度为0.7,隶属于矮的程度为0.2。
那么,逻辑前件的逻辑值为0.2,此时仍然需要对逻辑后件进行操作。由于,此时逻辑前件的值为0.2,是一个较小的值。那么我们可以作出的建议是,适量运动。
关于输出的语义变量和隶属度函数
到目前为止,我们已经完全了解了系统输入,输入的语义变量划分,隶属度函数刻画。同样地,对于系统的输出,我们仍然需要进行一个刻画。
对于一个给定的系统,其输出也是一个数值,而不同的数值区间也能进行不同的刻画。举例
| 输出变量 | 划分 |
|---|---|
| 建议 | 强烈地建议、基础性建议、不建议 |
| 锻炼频率 | 频繁、经常、偶尔、从不 |
| … | … |
仍然以上节的规则举例:
if 张三体重== 胖&&身高 ==矮 then 建议减肥
我们将建议程度通过数值区间[0 10]进行划分。那么,在逻辑前件为0.2的时候,我们的建议意见是多少呢?
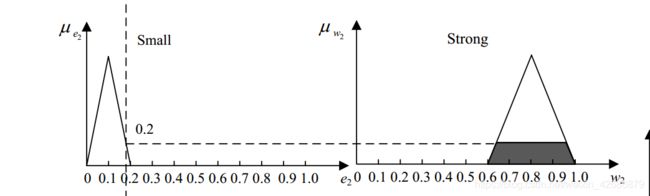
从示意图中可以看见,当前件隶属度为0.2时,表明前件在0.2的程度上满足逻辑后件。那么在逻辑后件的隶属度函数中,找到0.2隶属度对应的阴影部分面积。进而可以通过反模糊的方法可以求出输出的值。也就是建议的数值大小。
多条规则下的模糊推理系统
通常情况下,一个系统的模糊规则不止一条,也不应该只有一条。本节使用matlab给定的例子进行分析。根据餐厅服务和食物口感给小费多少的示例
| 变量 | 语义变量 | 区间 |
|---|---|---|
| 输入变量1:Service | poor,good,excellent | [0 10] |
| 输入变量2:food | rancid,delicious | [0 10] |
| 输出变量1:tip | cheap,average,generous | [0 30] |
并设定了如下三条规则
'1. If (service is poor) or (food is rancid) then (tip is cheap) (1) ’
'2. If (service is good) then (tip is average) (1) ’
‘3. If (service is excellent) or (food is delicious) then (tip is generous) (1)’
逻辑表示
'1. (service== poor) | (food == rancid) => (tip=cheap) (1) ’
'2. (service == good) => (tip=average) (1) ’
‘3. (service== excellent) | (food == delicious) => (tip=generous) (1)’
通过命令plotmf()得到输入、输出的语义变量对应的隶属度函数如下

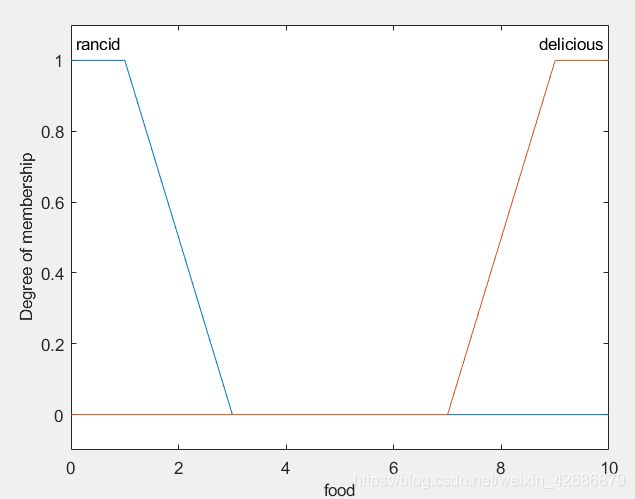

那么,对于任一给定的两个输入[service food],我们可以得到其对应的模糊化的隶属度。


从上面的两个图中,可以看出来:
- service对应于三个语义变量,隶属度分别为poor:0.02 good:0.85 excellent:0
- food对应于三个语义变量,隶属度分别为rancid:0.3 delicious:0
进而可以得到三个规则的逻辑前件值分别为
rule1: max(0.02,0.3)=0.3
rule2: 0.85
rule3: max(0,0)=0
对应于输出语义变量的隶属度为
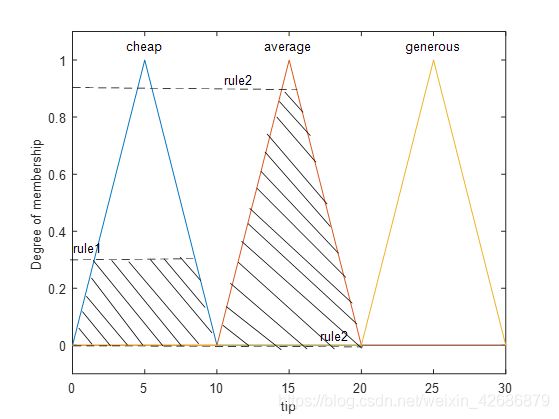
图中的阴影部分面积就是三个规则分别对应的输出。
最后对所有的输出结果做一个centroid运算,也就是将所有阴影面积组合起来,求其重心的横坐标。这个横坐标的值就是系统的最终输出。而这一步操作叫做去模糊化。
在实际操作过程中,有多种可供选择的去模糊化的方法。分别为
- ‘centroid’ — Centroid of the area under the output fuzzy set. This method is the default for Mamdani systems.
- ‘bisector’ — Bisector of the area under the output fuzzy set
- ‘mom’ — Mean of the values for which the output fuzzy set is maximum
- ‘lom’ — Largest value for which the output fuzzy set is maximum
- ‘som’ — Smallest value for which the output fuzzy set is maximum
从零开始实现一个模糊推理系统
目前为止,对模糊推理系统的介绍已经差不多了。下一部分就准备从零开始实现一个模糊推理系统。用于判定用户对于一个商品的购买决策。系统的输入,输出以及相应规则设定如下
- 系统输入为两个,分别为商品评价、用户购买意愿。输入范围都是[0 10]
- 系统输出为用户行为,购买与否。用[0 1]区间的数值表示。大于0.5则为购买。
- 模糊规则考虑为
- rule1: IF 购买意愿很强 THEN ACtion=买
- rule2: IF 商品评价极好且购买意愿为不为弱 THEN Action=买
- rule3: IF 商品评价为差 THEN Action=不买
- rule4: IF 如果商品评价不为差且购买意愿强 THEN Action=买
在下一节中,我们将从零开始实现这一模糊推理系统。