图机器学习 - cs224w Lecture 1 & 2 - 图的性质及随机图
文章目录
-
- Lecture 1: Introduction
- Lecture 2: Properties and Random Graph
-
- Degree Distribution
- Path Length
- Clustering Coefficient
- Connectivity
- Erdos-Renyi Random Graph Model
- Small-World Model
- Kronecker Graph Model
最近在看 Stanford 的 Machine Learning with Graphs。然后在网上找相关的笔记或者其他人的理解,发现大部分内容是照搬并翻译 slides, 没有一些个人的理解,而且很多地方只有前几个 lecture。所以打算自己整理一个系列的笔记供以后反复温习,也欢迎大家指正,共同学习。
Lecture 1: Introduction
Jure 提出了两个概念 Network 和 Graph,这两者的界限很模糊,但大致上我们可以将 Network 视为现实中的图,而 Graph 是一种更数学的描述方式。在很多复杂的系统之下都有错综复杂的关系网,比如食物链、化学物质的相互反应等。
课程标题很明确的表示了这个学科研究的是图,那么怎么研究。主要通过4个方面:
- node classification
- link prediction
- community detection
- network similarity
每一个方面后面当然会涉及到,所以即使现在不知所云也请稍安勿躁。
之前学的关于图的知识都没有进行这样的划分,但 Jure 提到这里不同的术语之间有微妙的区别(虽然感觉不是那么重要):
| Objects | Interactions | System |
|---|---|---|
| nodes | links | network |
| vertices | edges | graph |
| N N N | E E E | G ( N , E ) G(N,E) G(N,E) |
其他的关于图的基本知识不再赘述,不清楚的朋友可以先去温习一下图的基础部分。
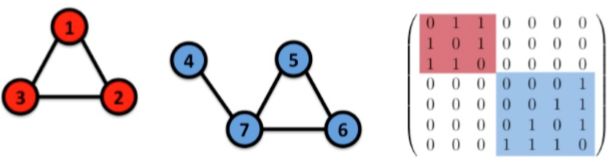
对于无向图的连通性有个有趣的现象之前没有注意过:若按一定顺序排列节点用邻接矩阵表示图的话,非连通图是严格的对角分块矩阵。
Lecture 2: Properties and Random Graph
描述一个图的特征一般有这样几个:
- degree distribution: P ( k ) P(k) P(k)
- path length: h h h
- clustering coefficient: C C C
- connected components: s s s
Degree Distribution
简单来说就是度的直方图,归一化后就是: P ( k ) = N k / N P(k)=N_k / N P(k)=Nk/N。 N k N_k Nk 是有 k k k 个度的节点个数。
一般来说,图的度分布是倾斜的,因此在可视化的时候可以选择用对数坐标,即 1 0 1 , 1 0 2 , 1 0 3 . . . 10^1, 10^2, 10^3 ... 101,102,103...
Path Length
一般意义上,路径长度指两个节点间的最短路径。而一个图中最长的最短路径定义为这个图的直径(diameter)。然而某些奇奇怪怪的图可能会有一条很长很长很长的路径,那么会导致直径很大。这样会对图的描述产生倾斜或者说是偏差,因此一般用平均路径长度来描述路径长度。
h ˉ = 1 2 E m a x ∑ i , j ≠ i h i j \bar{h}=\frac1{2E_{max}}\sum_{i,j \neq i}h_{ij} hˉ=2Emax1i,j=i∑hij
E m a x E_{max} Emax 是最大可能的边数,即 ( n − 1 ) n / 2 (n-1)n/2 (n−1)n/2。然而一般地,只计算存在的边算,而忽略不相通的节点对。
Clustering Coefficient
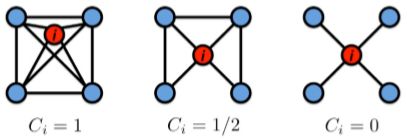
这个特征是用来衡量一个节点周围的邻接节点的互连关系的,简单来说就是一个节点的一个邻接节点多大程度上了解其他邻接节点。表示为
C i = 2 e i k i ( k i − 1 ) C_i=\frac{2e_i}{k_i(k_i-1)} Ci=ki(ki−1)2ei
e i e_i ei 是节点 i i i 的邻接节点之间的边的数量
Connectivity
连通性这个概念很广泛,包括连通子图的个数、最大连通子图的大小等
在有了这些衡量一个图的特征后,这些指标对我们来说只是一串数字而已。我们想知道这些值是“情理之中”还是“意料之外”,那么就需要一个参照来进行对比。
Erdos-Renyi Random Graph Model
这是一种最简单的随机图模型,它有两种定义方式:
- 给定 n n n 个节点,然后按同一概率 p p p 去生成每组节点对的边
- 给定 n n n 个节点,按均匀分布选 m m m 条边
那么通过这样的模型产生的随机图有怎样的性质呢?
Degree Distribution
度的分布服从伯努利分布,即
P ( k ) = ( n − 1 k ) p k ( 1 − p ) n − k − 1 P(k)=\begin{pmatrix}n-1\\k\end{pmatrix}p^k(1-p)^{n-k-1} P(k)=(n−1k)pk(1−p)n−k−1
那么根据伯努利分布的性质,其均值和方差分别为
- k ˉ = p ( n − 1 ) \bar{k}=p(n-1) kˉ=p(n−1)
- σ 2 = p ( 1 − p ) ( n − 1 ) \sigma^2=p(1-p)(n-1) σ2=p(1−p)(n−1)
这里 slide 上给出了一个表达式
σ k ˉ = [ 1 − p p 1 n − 1 ] 1 / 2 \frac{\sigma}{\bar{k}}=\big[\frac{1-p}p\frac1{n-1}\big]^{1/2} kˉσ=[p1−pn−11]1/2
Jure 的原话是:you can then ask how does the variance change as a function of the average degree.
也就是说这里服从大数定理,当图的规模足够大时,度的分布会变得很“窄”,即可以视作所有节点都有 k ˉ \bar{k} kˉ 的度
Clustering Coefficient
根据 clustering coefficient 的定义,我们需要知道节点的邻接节点间的边的数量。由于在 ER 随机图中边是 i.i.d. 的,所以期望为
E [ C i ] = E [ e i ] k i ( k i − 1 ) = p k i ( k i − 1 ) 2 k i ( k i − 1 ) = p = k ˉ n − 1 ≈ k ˉ n E[C_i]=\frac{E[e_i]}{k_i(k_i-1)}=\frac{p\frac{k_i(k_i-1)}{2}}{k_i(k_i-1)}=p=\frac{\bar{k}}{n-1}\approx\frac{\bar{k}}{n} E[Ci]=ki(ki−1)E[ei]=ki(ki−1)p2ki(ki−1)=p=n−1kˉ≈nkˉ
也就是说,随着图的规模增大,clustering coefficient 的值不断减小。
Path Length
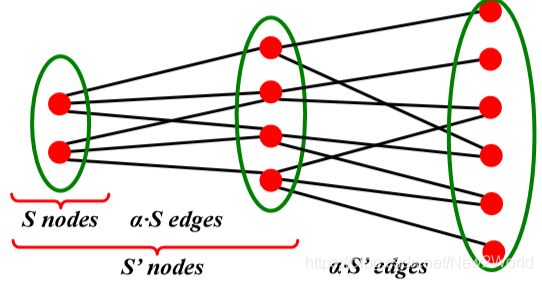
在讨论路径长度之前要先引入一个概念:Expansion α \alpha α
∀ S ⊆ V : # ( e d g e s l e a v i n g S ) ≥ α min ( ∣ S ∣ , ∣ V \ S ∣ ) \forall S \sube V:\#(edges\ leaving\ S)\geq\alpha\min(|S|,|V\text{\textbackslash}S|) ∀S⊆V:#(edges leaving S)≥αmin(∣S∣,∣V\S∣)
这个定义很数学,通俗地解释就是把一个图的节点分成两堆,使得连接两部分的边最少。那么通过这个我们怎么推导路径呢?
我们先回忆下 BFS 的工作原理,如下图,从一个点出发开始遍历整个图。如果图是连通的,那么第二层应该是初始点的邻接点,然后依次展开直到覆盖图中所有点。假设遍历的是这里的 ER 随机图,那么这棵树的深度就应该是 log n p n = log n / log n p \log_{np}n=\log n / \log np lognpn=logn/lognp
但这里没有涉及到 expansion 这个概念呀!应该说没有显示地说明这个概念,因为我们限制了 ER 图。更一般的图的度不一定是 n p np np,因此需要用 expansion 的 α \alpha α 来替换这里特殊的 average degree。如此一来,将平均路径长度推广为 O ( ( log n ) / α ) O((\log n) / \alpha) O((logn)/α)
Connectivity
在边的概率 p p p 逐渐增大过程中可以发现,当 p = 1 / ( n − 1 ) p=1/(n-1) p=1/(n−1) 时,即平均度为 1 1 1 时,giant component 开始出现。
这样我们就有了一个可以与真实网络进行对比的模型了
- average path length
- giant connected component
- clustering coefficient
- degree distribution
通过对比我们可以发现这个随机图模型的特征只在路径长度和最大连通子图上和真实网络差不多,但其余性质上差得很远。这样也说明了真实世界的网络不是随机的,其背后有复杂的关系等待我们去发现。
Small-World Model
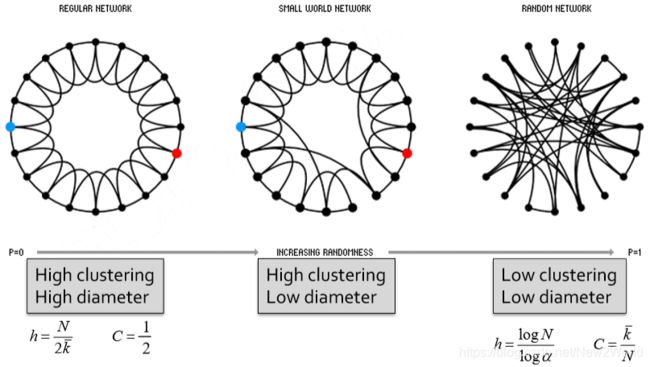
通过对 ER 图的分析我们发现这种简单的随机图丢失了聚类信息,即 local structure。然而,单纯的加上 local connections 会导致图的平均路径增加而破坏我们原本已经吻合了的性质。因此提出了这个 Small-World 模型。
这里 Jure 对为什么 triadic closure 会导致网络直径增加的解释有点不清楚。按理说朋友的朋友就是我的朋友这一点能缩短路径长度呀。我的理解是这里应该突出的是 local 这一条件。以交通网为例,如果现在只有相邻城市间有交通线路,那么我从四川到北京就得途经“四川-陕西-山西-河北-北京”。但如果我有四川到北京的直飞线路呢?那直观上不就直接“四川-北京”了吗。
这个 Small-World 模型首先为了确保有 local structure,将自己初始化为下图的样子(regular ring lattice)。然后依概率将一条边的一个端点连接到任意一个不同节点上。如此,初始化保证了 clustering coefficient,而 rewiring 引入了随机性从而缩减了网络直径。

但是这里需要注意的是如果 rewiring 的概率太高或太低都不行。
Kronecker Graph Model
这个模型有两个突出的优势
- 可并行,快,适合生成大规模的图
- 遵从一些真实网络的“规则”
Idea:递归地生成一张图
每个公司内都有很多部门,各个部门有管理层和不同的事业群,每个事业群内又有组长和员工。这样的结构在大部分公司里都差不多。那么推广这个规律,我们先定义一个小群体内的网络结构,然后递归地使用这样的结构来构建更大的图。
定义 Kronecker product
C = A ⊗ B ≐ ( a 1 , 1 B a 1 , 2 B . . . a 1 , m B a 2 , 1 B a 2 , 2 B . . . a 2 , m B . . . . . . a n , 1 B a n , 2 B . . . a n , m B ) C=A \otimes B \doteq \begin{pmatrix} a_{1,1}B & a_{1,2}B & ... & a_{1,m}B \\ a_{2,1}B & a_{2,2}B & ... & a_{2,m}B \\ & ... & ... \\ a_{n,1}B & a_{n,2}B & ... & a_{n,m}B \end{pmatrix} C=A⊗B≐⎝⎜⎜⎛a1,1Ba2,1Ban,1Ba1,2Ba2,2B...an,2B............a1,mBa2,mBan,mB⎠⎟⎟⎞
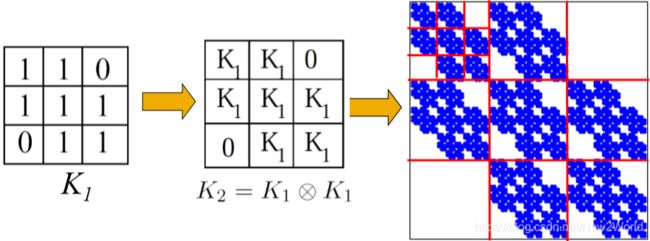
如果用邻接矩阵来直接生成那太死板了,所以为引入随机性将邻接矩阵换成概率矩阵,即矩阵的每个元素表示对应节点对右边的概率。这样通过 Kronecer product 最终得到整个网络的边的概率分布图。然后我们再通过每个区域的概率递归地选择边来得到图的一个 realization。
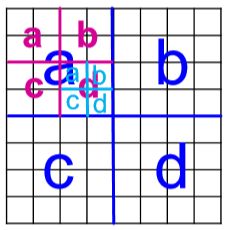
这种方法选边时不可避免地会遇到重复边,但概率很小。就算遇到了,reinsert 就行了,无伤大雅。
需要确定边的条数,而这一般依赖经验
实验证明 Kronecker 图在各种性质上都能较好地拟合真实的网络。但这个模型生成的图的 degree distribution 并不是平滑的。直观上说,按初始定义的 block structure 进行递归所得到的图可能的确存在这个问题,即某些部分连接紧密有些地方稀疏,而这种差异并不连续。