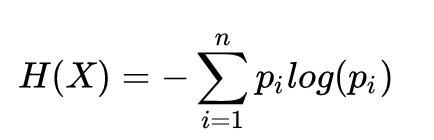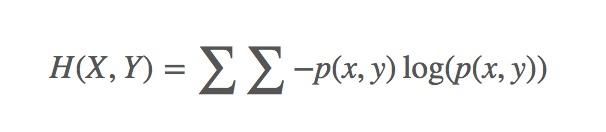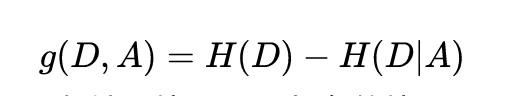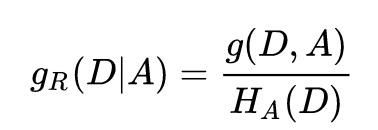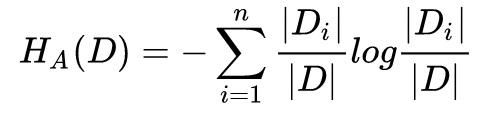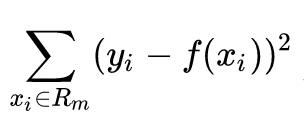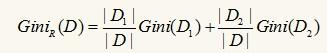python数据挖掘决策树算法_数据挖掘——决策树巩固与 Python 实现
上个星期去崇州参加比赛,回来老师已经讲到了「分类」,那一节课学了决策树,现在继续课后巩固一下。
什么是决策树
概念
决策树(decision tree)是一种类似于流程图的树结构(可以是二叉树也可以不是),其中,每个内部节点(非叶子结点)表示在一个属性上的测试,每个分枝代表该测试的一个输出,而每个叶子结点存放一个类标号。书的最顶层节点是根节点。
决策树是一种基本的分类与回归方法,它可以看作if-then规则的集合,也可以认为是定义在特征空间与类空间上的条件概率分布。
更好的理解
以一个例子更好的理解决策树:
上面这个例子,就是用来决策顾客是否可能购买计算机。每个内部节点表示在一个属性上的测试(比如是否是学生),而每个叶子结点存放一个类标号也就是决策结果(比如 buys_computer = no/yes),箭头表示一个判断条件在不同情况下的决策路程。
决策树可以运用在诸多领域。
决策树学习算法构成
主要构成有三个部分:
特征选择
决策树生成
决策树的剪枝
决策树的路径具有一个重要的性质:互斥且完备,即每一个样本均被且只能被一条路径所覆盖。
特征选择
如果利用一个特征进行分类的结果与随机分类的结果无异,则可以认为这个特征是不具备分类能力的。把这样的特征去掉,对决策树的分类精度应该影响不大。
那如何判断一个特征的分类能力呢?比如说在上面那个图中,为什么将age属性作为第一个分类,而不是student或者credit_rating呢?
这就需要「信息增益」这个概念,需要一些准备知识。
熵(entropy)
熵表示随机变量的不确定性,熵值越大表示随机变量含有的信息越少,变量的不确定性越大。 随机变量 X 的熵的表达式为:
P(X = xi) = pi,i = 1, 2, …, n,是 X 的概率分布。
联合熵
上面那个是一个变量 X 的熵,多个变量的联合熵,比如两个变量 X 和 Y 的联合熵表达式为:
联合熵是一集变量之间不确定性的衡量手段。
条件熵
随机变量X给定的条件下,随机变量Y的条件熵H(Y|X)定义为:
信息增益(information gain):
信息增益是指:得知特征 X 的信息而使得类 Y 的信息的不确定性减少的程度。
特征 A 对训练集 D 的信息增益记为g(D, A),定义为集合 D 的经验熵H(D),与特征 A 给定条件下 D 的熵H(D|A)之差,即:
根据信息增益准则进行特征选择的方法是:对训练数据集D,计算其每个特征的信息增益,并比它们的大小,从而选择信息增益最大的特征。
信息增益比(information gain ratio)
以信息增益作为特征选择准则,会存在偏向于选择取值较多的特征的问题。可以采用信息增益比对这一问题进行校正。
特征 A 对训练集 D 的信息增益比定义为其信息增益与训练集 D 关于特征 A 的值的熵之比,即
其中,
决策树的生成
决策树的生成算法有很多变形,这里介绍几种经典的实现算法:ID3 算法,C4.5 算法以及 CART 算法。这些算法的主要区别在于分类结点上特征选择的选取标准不同。下面详细了解一下算法及其具体实现过程。
具体例题可参考《数据挖掘概念与技术》一书。
数据
数据来源于《数据挖掘概念与技术》书中。以下实现均基于这个数据。
RID
age
income
student
credit_rating
Class: buys_computer
1
youth
high
no
fair
no
2
youth
high
no
excellent
no
3
middle_aged
high
no
fair
yes
4
senior
medium
no
fair
yes
5
senior
low
yes
fair
yes
6
senior
low
yes
excellent
no
7
middle_aged
low
yes
excellent
yes
8
youth
medium
no
fair
no
9
youth
low
yes
fair
yes
10
senior
medium
yes
fair
yes
11
youth
medium
yes
excellent
yes
12
middle_aged
medium
no
excellent
yes
13
middle_aged
high
yes
fair
yes
14
senior
medium
no
excellent
no
ID3 算法及实现
ID3 算法的核心是在决策树各个结点上应用信息增益准则进行特征选择。
从根节点开始,对结点计算所有可能特征的信息增益,选择信息增益最大的特征作为结点的特征,并由该特征的不同取值构建子节点;
对子节点递归地调用以上方法,构建决策树;
直到所有特征的信息增益均很小或者没有特征可选时为止。
Python 实现
# 待更
C4.5 算法及实现
由 ID3 算法演化而来。
C4.5 算法与 ID3 算法的区别主要在于它在生产决策树的过程中,使用信息增益比来进行特征选择。
Python 实现
# 待更
CART 算法及实现
由 ID3 算法演化而来。
CART 算法假设决策树是一颗二叉树,它通过递归地二分每一个特征,将特征区间划分为有限个单元,并在这些但愿上确定预测的概率分布。
CART 算法中,对于回归,采用的是「平方误差最小化」准则;对于分类,采用的是「基尼指数最小化」准则。
平方误差最小化
假设已将输入空间划分为 M 个单元,并且在每个单元 R1, R2, …, Rm,并且在每个 单元 Rm 上有一个固定的输出值 Cm ,于是回归树可以表示为:
当输入空间的划分确定时,可以用平方误差
来表示回归树对于训练数据的预测误差。
基尼指数
这里讲的是分类,所以先重点了解基尼指数。
基尼指数是度量数据分区和训练元组集 D 的不纯度。
假设有 m 个类别,样本点属于第 i 类的概率为 Pi,则概率分布的基尼指数定义为:
对每个属性,需要考虑每种可能的二元化分。对于离散值属性,选择该属性产生最小基尼指数的子集作为它的分裂子集。而对于连续值属性,必须考虑每个可能的分裂点。
对于样本 D,如果根据特征 A 的某个值 a,把 D 分成 D1 和 D2 两部分,则在特征 A的条件下,D 的基尼系数表达式为:
对于离散或连续值属性 A 的二元划分导致的不纯度降低为:
![]()
选择产生最小基尼指数的属性作为分裂属性。
Python 实现
# 待更
决策树的剪枝
# 待更