吴恩达深度学习课程笔记之卷积神经网络（2nd week）

0 参考资料

[1]  大大鹏/Bilibili资料 - Gitee.com

[2] 【中英字幕】吴恩达深度学习课程第四课 — 卷积神经网络_哔哩哔哩_bilibili

[3]  深度学习笔记-目录 (ai-start.com)

1 为什么要进行实例探究？（Why look at case studies?）

就像很多人通过看别人的代码来学习编程一样，学习深度学习最直观的方式之一就是去看一些案例。过去几年计算机视觉研究中的大量研究都集中在如何把一些基本构件组合起来，形成有效的卷积神经网络。通过研究别人的架构来构建自己有效组件的办法比较高效，实际上在计算机视觉任务中表现良好的神经网络框架往往也适用于其它任务。也就是说，如果有人已经训练或者计算出擅长识别猫、狗、人的神经网络或者神经网络框架，现在需要构建一个自动驾驶汽车的框架，那么完全可以借鉴别人的神经网络框架来解决自己的问题。 

本文将围绕经典网络中的LeNet-5、AlexNet、VGG-16，ResNet以及Inception神经网络进行实例分析，然后还会介绍如何使用开源资源实现神经网络搭建、迁移学习以及数据增强的方法，最后总结了一下计算机视觉的现状。

2 经典网络（Classic networks）

2.1 LeNet-5

假设有一张32×32×1的图片，LeNet-5可以识别图中的手写数字，比如像这样手写数字7。LeNet-5是针对灰度图片训练的，所以图片的大小只有32×32×1。实际上LeNet-5的结构使用了6个5×5的过滤器，步幅为1。由于使用了6个过滤器，步幅为1，padding为0，则输出结果为28×28×6，图像尺寸从32×32缩小到28×28；然后进行平均池化操作，过滤器的宽度为2，步幅为2，图像的尺寸，高度和宽度都缩小了2倍，输出结果是一个14×14×6的图像。

接下来又是卷积层，现使用一组16个5×5的过滤器，步长为1，padding为0，故新的输出结果为10×10×16；再次进行平均池化操作，过滤器的宽度为2，步幅为2，图像的尺寸，高度和宽度又缩小了2倍，输出结果是一个5×5×16的图像。由于LeNet-5是较早的CNN技术，它总是使用valid卷积，每进行一次卷积，图像的高度和宽度都会缩小，所以这个图像从14到14缩小到了10×10；然后又是池化层，高度和宽度再缩小一半，输出一个5×5×16的图像。将所有数字相乘，乘积是400。

下一层是全连接层，在全连接层中，有400个节点，每个节点有120个神经元，也就是说这个全连接层会输出120个结果，在使用这120个结构构建另一个全连接层，此全连接层有120个节点，每个节点有84个神经元，在这两个全连接层的作用下输出84个结果。

最后一步就是利用这84个特征得到最后的输出，最后需要再加一个节点用来预测的值，由于有10个可能的值，对应识别0-9这10个数字，因此最后的输出应该是10个数字。现在通常使用softmax函数输出十种分类结果，但是以前的LeNet-5并不是采用的softmax函数。

随着LeNet-5网络越来越深，图像的高度和宽度在缩小，从最初的32×32缩小到28×28，再到14×14、10×10，最后只有5×5。与此同时，随着网络层次的加深，通道数量一直在增加，从1增加到6个，再到16个。

以现在的眼光来看，LeNet-5并不是十分高明，但是这个神经网络中还有一种模式至今仍然经常用到，那就是一个或多个卷积层后面跟着一个池化层，然后又是若干个卷积层再接一个池化层，然后是全连接层，最后是输出，这种排列方式很常用。

2.2 AlexNet

AlexNet的步骤：首先用一张227×227×3的图片作为输入第一层，使用96个11×11的过滤器，步幅为4；由于步幅是4，尺寸缩小到55×55，缩小了4倍左右；然后用一个3×3的过滤器构建最大池化层，步幅s为2，卷积层尺寸缩小为27×27×96；接着再执行一个5×5×256的same卷积，输出是27×27×276；然后再次进行最大池化，尺寸缩小到13×13×256；使用384个过滤器再执行一次same卷积，得到的结果是13×13×384；再做一次同样的操作，得到13×13×384；再使用256个过滤器做一次same卷积，得到13×13×256；最后再进行一次3×3的最大池化，步长为2，尺寸缩小到6×6×256。6×6×256等于9216，将其展开为9216个单元，然后是三个维度分别为9216,4096,4096的全连接层；最后使用softmax函数输出1000个识别的可能性，来判断究竟是1000个可能的对象中的哪一个。

实际上，AlexNet与LeNet-5有很多相似之处，不过AlexNet要大得多。LeNet-5大约有6万个参数，而AlexNet包含约6000万个参数。当用于训练图像和数据集时，AlexNet能够处理非常相似的基本构造模块，这些模块往往包含着大量的隐藏单元或数据。

经典的AlexNet结构还有另一种类型的层，叫作“局部响应归一化层”（Local Response Normalization），即LRN层，很多研究者发现LRN起不到太大作用，故这类层应用得并不多。

2.3 VGG-16

与AlexNet相比，VGG-16网络没有那么多超参数，这是一种只需要专注于构建卷积层的简单网络。首先用3×3，步幅为1的过滤器构建卷积层，padding参数为same卷积中的参数；然后用一个2×2，步幅为2的过滤器构建最大池化层。因此VGG网络的一大优点是它确实简化了神经网络结构，下面具体讲讲这种网络结构。

假设上面这个224×224×3的小图是输入图像，进行第一个卷积之后得到224×224×64的特征图，接着还有一层224×224×64，得到这样2个厚度为64的卷积层，这实际上意味着用64个过滤器进行了两次卷积。这里采用的都是大小为3×3，步幅为1的过滤器，并且都是采用same卷积，故不再把所有的层都画出来，只用一串数字代表这些网络。

接下来创建一个池化层，池化层将输入图像进行压缩，从224×224×64缩小到112×112×64。然后又是若干个卷积层，使用128个过滤器，以及一些same卷积，输出112×112×128；然后进行池化，可以推导出池化后的结果是这56×56×128；接着再用256个相同的过滤器进行三次卷积操作，然后再池化，然后再卷积三次，再池化。如此进行几轮操作后，将最后得到的7×7×512的特征图进行两次全连接操作，得到4096个单元，然后进行softmax激活，输出从1000个识别的可能。

顺便说一下，VGG-16的这个数字16，就是指在这个网络中包含16个卷积层和全连接层（池化和卷积算一层，softmax不算）。这确实是个很大的网络，总共包含约1.38亿个参数，即便以现在的标准来看都算是非常大的网络。但VGG-16的结构并不复杂，这点非常吸引人，而且这种网络结构很规整，都是几个卷积层后面跟着可以压缩图像大小的池化层，池化层缩小图像的高度和宽度。同时，卷积层的过滤器数量变化存在一定的规律，由64翻倍变成128，再到256和512。作者可能认为512已经足够大了，所以后面的层就不再翻倍了。无论如何，每一步都进行翻倍，或者说在每一组卷积层进行过滤器翻倍操作，正是设计此种网络结构的另一个简单原则。这种相对一致的网络结构对研究者很有吸引力，而它的主要缺点是需要训练的特征数量非常巨大。

随着VGG-16网络的加深，图像的高度和宽度都在以一定的规律不断缩小，每次池化后刚好缩小一半，而通道数量在不断增加，而且刚好也是在每组卷积操作后增加一倍。也就是说，图像缩小的比例和通道数增加的比例是有规律的。

3 残差网络（Residual Networks ）

非常非常深的神经网络是很难训练的，因为存在梯度消失和梯度爆炸问题。跳跃连接（Skip connection）可以从某一层网络层获取激活，然后迅速反馈给另外一层，甚至是神经网络的更深层。利用跳跃连接构建能够训练深度网络的ResNets，有时深度能够超过100层。

ResNets是由残差块（Residual block）构建的，首先解释一下什么是残差块。

这是一个两层神经网络，在层进行激活，得到，再次进行激活，两层之后得到。计算过程是从开始，首先进行线性激活，根据这个公式：，通过算出，即乘以权重矩阵，再加上偏差因子。然后通过ReLU非线性激活函数得到。接着再次进行线性激活，依据等式，最后根据再次进行ReLu非线性激活，这里的ReLU是指一个非线性函数，最后得到的结果就是。换句话说，信息流需要经过以上所有步骤。

在残差网络中有一点变化，现在将直接向前，拷贝到神经网络的深层，在ReLU非线性激活函数前加上，这是一条捷径。的信息直接到达神经网络的深层，不再沿着主路径传递，这就意味着最后这个等式()去掉了，取而代之的是另一个ReLU非线性函数，仍然对进行g函数处理，但这次要加上，即：，也就是加上的这个产生了一个残差块。

在上面这个图中，也可以画一条捷径直达第二层。实际上这条捷径是在进行ReLU非线性激活函数之前加上的，而这里的每一个节点都已经执行了线性函数、还未执行ReLU激活函数，所以插入的时机是在线性激活之后，ReLU激活之前。除了捷径，可能还会听到另一个术语“跳跃连接”，就是指跳过一层或者好几层，从而将信息传递到神经网络的更深层，他们指的其实是同一个操作。

ResNet的发明者是何凯明（Kaiming He）、张翔宇（Xiangyu Zhang）、任少卿（Shaoqing Ren）和孙剑西（Jiangxi Sun），他们发现使用残差块能够训练更深的神经网络。所以构建一个ResNet网络就是通过将很多这样的残差块堆积在一起，形成一个很深神经网络。

上图并不是一个残差网络，而是一个普通网络（Plain network），这个术语来自ResNet论文。把它变成ResNet的方法是加上所有跳跃连接，每两层增加一个捷径，构成一个残差块。如下图所示，5个残差块连接在一起构成一个残差网络

如果使用标准优化算法训练一个普通网络，比如说梯度下降法，或者其它热门的优化算法。如果没有残差，没有这些捷径或者跳跃连接，会发现随着网络深度的加深，训练错误会先减少，然后增多。而理论上，随着网络深度的加深，应该训练得越来越好才对。也就是说，理论上网络深度越深越好。但实际上，如果没有残差网络，对于一个普通网络来说，深度越深意味着用优化算法越难训练。实际上，随着网络深度的加深，训练错误会越来越多。

但有了ResNets就不一样了，即使网络再深，训练的表现却不错，比如说训练误差减少，就算是训练深达100层的网络也不例外。这种方式确实有助于解决梯度消失和梯度爆炸问题，在训练更深网络的同时，又能保证良好的性能。也许从另外一个角度来看，随着网络越来深，网络连接会变得臃肿，但是ResNet确实在训练深度网络方面非常有效。

4 残差网络为什么有用？（Why ResNets work?）

 一个网络深度越深，它在训练集上训练的效率就会有所减弱，这也是有时候不希望加深网络的原因。而事实并非如此，至少在训练ResNets网络时，并非完全如此，举个例子。

假设有一个大型神经网络，其输入为，输出激活值。假如想增加这个神经网络的深度，用Big NN表示，输出为。再给这个网络额外添加两层，依次添加两层，最后输出为，可以把这两层看作一个ResNets块，即具有捷径连接的残差块。为了方便说明，假设在整个网络中使用ReLU激活函数，所以激活值都大于等于0，包括输入的非零异常值。因为ReLU激活函数输出的数字要么是0，要么是正数。

看一下的值，也就是表达式，添加项是刚添加的跳跃连接的输入。展开这个表达式，其中。注意一点，如果使用L2正则化（控制模型复杂度，减小过拟合的一种技术）或权重衰减，它会压缩的值。如果对b应用权重衰减也可达到同样的效果。这里的W是关键项，如果，为方便起见，再假设，这几项就没有了，因为它们（）的值为0。最后（因为我们假定使用ReLU激活函数，并且所有激活值都是非负的，而且是应用于非负数的ReLU函数，所以）。

结果表明，残差块学习这个恒等式函数并不难，跳跃连接使得很容易得出。这意味着，即使给神经网络增加了这两层，它的效率也并不逊色于更简单的神经网络，因为学习恒等函数对它来说很简单。尽管它多了两层，也只把的值赋值给。所以给大型神经网络增加两层，不论是把残差块添加到神经网络的中间还是末端位置，都不会影响网络的表现。

当然，不仅仅是保持网络的效率，还要提升它的效率。想象一下，如果这些隐藏层单元学到一些有用信息，那么它可能比学习恒等函数表现得更好。而这些不含有残差块或跳跃连接的深度普通网络情况就不一样了，当网络不断加深时，就算是选用学习恒等函数的参数都很困难，所以很多层最后的表现不但没有更好，反而更糟。

残差网络起作用的主要原因就是这些残差块学习恒等函数非常容易，网络性能不会受到影响，很多时候甚至可以提高效率，或者说至少不会降低网络的效率，因此创建类似残差网络可以提升网络性能。

除此之外，关于残差网络，另一个值得探讨的细节是，假设与具有相同维度，所以ResNets使用了许多same卷积，所以这个的维度等于这个输出层的维度。之所以能实现跳跃连接是因为same卷积保留了维度，所以很容易得出这个捷径连接，并输出这两个相同维度的向量。

如果输入和输出有不同维度，比如输入的维度是128，的维度是256，再增加一个矩阵，这里标记为，是一个256×128维度的矩阵，所以的维度是256，这个新增项是256维度的向量。不需要对做任何操作，它是网络通过学习得到的矩阵或参数，它是一个固定矩阵，padding值为0，用0填充，其维度为256。

最后，来看看ResNets的图片识别。下图是一个普通网络，给它输入一张图片，它有多个卷积层，最后是一个池化层，之后再连接一个全连接层，最后通过Softmax函数输出了1000个可能性。

如何把它转化为ResNets呢？只需要添加跳跃连接。这里只讨论几个细节，这个网络有很多层3×3卷积，而且它们大多都是same卷积，这就是添加等维特征向量的原因。因为它们都是same卷积，维度得以保留，这也解释了添加项（维度相同所以能够相加）。

ResNets类似于其它很多网络，也会有很多卷积层，其中偶尔会有池化层或类池化层的层。不论这些层是什么类型，都需要调整矩阵的维度（维度相同才能相加)。普通网络和ResNets网络常用的结构是：卷积层-卷积层-卷积层-池化层-卷积层-卷积层-卷积层-池化层……依此重复。直到最后，有一个通过softmax进行预测的全连接层。

5 网络中的网络或 1×1 卷积（Network in Network or 1×1 convolutions）

在架构内容设计方面，其中一个比较有帮助的想法是使用1×1卷积。下面使用一个实例来解释1×1的卷积作用。

过滤器为1×1（这里是数字2），输入一张6×6×1的图片，然后对它做卷积，过滤器大小为1×1×1，结果相当于把这个图片乘以数字2，所以前三个单元格分别是2、4、6等等。用1×1的过滤器进行卷积，似乎用处不大，只是对输入矩阵乘以某个数字。但这仅仅是对于6×6×1的一个通道图片来说，1×1卷积效果不佳。

如果是一张6×6×32的图片，那么使用1×1过滤器进行卷积效果更好。具体来说，1×1卷积所实现的功能是遍历这36个单元格，计算左图中32个数字和过滤器中32个数字的元素积之和，然后应用ReLU非线性函数。

以其中一个单元为例，它是这个输入层上的某个切片，用这36个数字乘以这个输入层上1×1切片，得到一个实数。这个1×1×32过滤器中的32个数字可以这样理解，一个神经元的输入是32个数字（输入图片中左下角位置32个通道中的数字），即相同高度和宽度上某一切片上的32个数字，这32个数字具有不同通道，乘以32个权重（将过滤器中的32个数理解为权重），然后应用ReLU非线性函数，在这里输出相应的结果。

一般来说，如果过滤器不止一个，而是多个，就好像有多个输入单元，其输入内容为一个切片上所有数字，输出结果是6×6过滤器数量。

所以1×1卷积可以从根本上理解为对这32个不同的位置都应用一个全连接层，全连接层的作用是输入32个数字（过滤器数量标记为，在这36个单元上重复此过程），输出结果是6×6×，以便在输入层上实施一个非平凡（non-trivial）计算。 

这种方法通常称为1×1卷积，有时也被称为Network in Network。下面举个1×1卷积的应用例子。

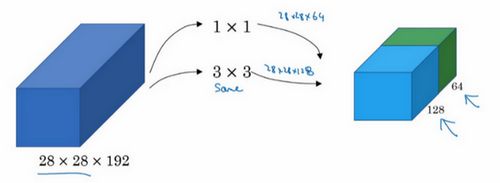
假设这是一个28×28×192的输入层，可以使用池化层压缩它的高度和宽度，但如果通道数量很大，该如何把它压缩为28×28×32维度的层呢？可以用32个大小为1×1×192的过滤器，此过滤器的输出层为28×28×32，这就是压缩通道数（）的方法，对于池化层只是压缩了这些层的高度和宽度。当然如果想保持通道数不变甚至更多，这也是可行的，使用其他数量的过滤器即可。另外，1×1卷积只是添加了非线性函数，当然也可以让网络学习更复杂的函数。总之，可以使用池化层压缩图片的高度和宽度，而要压缩图片的通道数，需要使用1×1卷积。

6 Inception 模块简介（Inception module profile）

构建卷积层时，需要决定过滤器的大小究竟是1×1，3×3还是5×5，或者要不要添加池化层。而Inception网络的作用就是决定如何选择过滤器大小，虽然网络架构因此变得更加复杂，但网络表现却非常好，下面来了解一下其中的原理。

例如，这是一个28×28×192维度的输入层，Inception网络或Inception层的作用就是代替人工来确定卷积层中的过滤器类型，或者确定是否需要创建卷积层或池化层，下面来演示一下。

如果使用1×1×64卷积，输出为28×28×64，并且这里只有一个层。如果使用3×3×128的过滤器，且进行same卷积，那么输出是28×28×128；然后把第二个值堆积到第一个值上。

再使用用5×5过滤器，且为same卷积，输出变成28×28×32；然后把第三个值堆积到第二个值上。

除了卷积操作以外，还可以使用池化操作，这里的池化输出是28×28×32。为了匹配所有维度，需要对最大池化使用padding，且步幅为1，然后将输出结果再次堆叠起来。

对于这样的Inception模块，若输入为28×28×192，则输出为28×28×256（因为叠加了4层，输入一个数据，就会有32+32+128+64=256个输出）。Inception网络不需要人为决定使用哪个过滤器或者是否需要池化，而是由网络自行确定这些参数，可以给网络添加这些参数的所有可能值，然后把这些输出连接起来，让网络自己学习它需要什么样的参数，采用哪些过滤器组合。

不难发现，Inception层有一个问题，就是计算成本可能会很高，下面以一个5×5过滤器在该模块中的计算成本为例。

这是一个28×28×192的输入块，执行一个5×5卷积，它有32个过滤器，输出为28×28×32。现在计算这个28×28×32输出的计算成本。它有32个过滤器，每个过滤器大小为5×5×192，输出大小为28×28×32，所以要计算28×28×32个数字。对于输出中的每个数字来说，都需要执行5×5×192次乘法运算，所以乘法运算的总次数为每个输出值所需要执行的乘法运算次数（5×5×192）乘以输出值个数（28×28×32），把这些数相乘结果等于1.2亿(120422400)。即使在现在，用计算机执行1.2亿次乘法运算，成本也是相当高的。

这里还有另外一种架构，其输入为28×28×192，输出为28×28×32。其结构是这样的，对于输入层，使用1×1卷积把输入值从192个通道减少到16个通道。然后对这个较小层运行5×5卷积，得到最终输出。注意，输入和输出的维度依然相同，输入是28×28×192，输出是28×28×32，它只有32个通道，而不是192个。本架构做的就是把左边这个大的输入层压缩成右边这个较小的的中间层。

上图这一层有时候这被称为瓶颈层，所谓的瓶颈通常是某个对象最小的部分，假如有这样一个玻璃瓶，这是瓶塞位置，瓶颈就是这个瓶子最小的部分；同理，瓶颈层也是网络中最小的部分，先缩小网络然后再扩大它。

接下来看看带瓶颈结构网络的计算成本。应用1×1卷积，过滤器个数为16，每个过滤器大小为1×1×192，这两个维度相匹配（输入通道数与过滤器通道数），28×28×16这个层的计算成本是，输出28×28×192中每个元素都做1×1×192次乘法，相乘结果约等于240万。

240万只是第一个卷积层的计算成本，对于第二个卷积层，输出为28×28×32，对每个输出值应用一个5×5×16维度的过滤器，计算结果为1000万。

所以所需要乘法运算的总次数是这两层的计算成本之和，也就是1204万，计算成本从1.2亿下降到了原来的十分之一，即1204万（所需要的加法运算与乘法运算的次数近似相等，故只统计了乘法运算的次数）。

总结一下，如果在构建神经网络层的时候，不想决定池化层是使用1×1，3×3还是5×5的过滤器，那么Inception模块就是最好的选择。Inception模块可以应用各种类型的过滤器，只需要把输出连接起来。还可以通过使用1×1卷积来构建瓶颈层，来大大降低计算成本。另外，只要合理构建瓶颈层，既可以显著缩小表示层规模，又不会降低网络性能，从而节省了计算。

7 Inception 网络（Inception network）

在上节介绍了Inception网络基础模块。本节将这些模块组合起来，构筑成为Inception网络。

Inception模块会将之前层的激活或者输出作为它的输入，以一个28×28×192的输入为例，先通过一个1×1的卷积层，再通过一个5×5的卷积层，其中，1×1的卷积层有16个通道，而5×5的卷积层输出为28×28×32，共32个通道。

为了在这个3×3的卷积层中节省运算量，也可以做相同的操作，不过1×1的卷积层有96个通道，而3×3的卷积层有128个通道，这样的话3×3的层将会输出28×28×128。

还可以直接通过一个1×1×64的卷积层，这时就不必在后面再跟一个1×1的层了，这样的话过程就只有一步，这个层的输出是28×28×64。

最后是池化层。

为了能在最后将这些输出都连接起来，会使用same类型的padding来池化，使得输出的高和宽依然是28×28，这样才能将它与其他输出连接起来。但注意，对于最大池化，即便用了same padding，3×3的过滤器，stride为1，其输出将会是28×28×192，其通道数或者说深度与这里的输入（通道数）相同；所以看起来它会有很多通道，需要再加上一个1×1的卷积层，将通道的数量缩小到28×28×32，也就是使用32个维度为1×1×192的过滤器，所以输出的维度其通道数缩小为32。这样就避免了最后输出时，池化层占据所有的通道。

最后，将这些方块全都连接起来。在这个过程中，把得到的各个层的通道都加起来，最后得到一个28×28×256的输出（64+128+32+32=256）。通道连接实际就是把所有方块连接在一起。上图所示的就是一个Inception模块，而Inception网络所做的就是将这些模块都组合到一起。

上图是一张关于Inception网络的图片，整张图看上去很复杂，但其实本质来说就是不同的Inception模块拼接在一起。

事实上在Inception网络还存在一些分支。在网络的最后几层，通常称为全连接层，在它之后是一个softmax层（编号1）来做出预测，编号为2的分支所做的就是通过隐藏层（编号3）来做出预测，所以这其实也是一个softmax输出（编号2）。编号4也包含了一个隐藏层，再通过一些全连接层，然后有一个softmax来预测，输出结果的标签。应该把这些合分支看做Inception网络的一个细节，它确保了隐藏单元和中间层（编号5）也参与了特征计算，它们也能预测图片的分类，在Inception网络中，起到一种调整的效果，并且能防止网络发生过拟合。

此外，还有一个由Google公司研发的Inception网络，它被叫做GoogleLeNet，这个名字是为了向LeNet网络致敬。

最后总结一下，理解了Inception模块之后，再来理解Inception网络就比较简单，它无非是很多个Inception模块一环接一环，最后组成了网络。自从Inception模块诞生以来，经过研究者们的不断发展，衍生了许多新的版本，比如Inception V2、V3以及V4，还有一个版本引入了跳跃连接的方法，有时也会有特别好的效果，但所有的这些变体都建立在同一种基础的思想上。

8 使用开源的实现方案（Using open-source implementations）

事实证明很多神经网络复杂细致，因而难以复制，因为一些参数调整的细节问题，例如学习率衰减等等，会影响性能。甚至在顶尖大学学习AI或者深度学习的博士生也很难通过阅读别人的研究论文来复制他人的成果。幸运的是有很多深度学习的研究者都习惯把自己的成果作为开发资源，放在像GitHub之类的网站上。

下面以残差网络为例讲解如何开源实现它的框架。首先搜索GitHub上的ResNets，然后就可以看到很多不同的ResNet的实现。打开第一个网址即可（ResNets实现的GitHub地址https://github.com/KaimingHe/deep-residual-networks），这是一个ResNets实现的GitHub资源库；在资源库网页由上往下翻，会看到一些描述这个实现的文字说明；点击页面的下载链接后就能够以压缩包的形式下载源代码。

在开发一个计算机视觉应用时，一个常见的工作流程是先选择一个喜欢的架构，接着在GitHub寻找一个开源实现，然后从GitHub上下载下来，以此基础开始构建。这样做的优点在于，这些网络通常都需要很长的时间来训练，而或许有人已经使用多个GPU，通过庞大的数据集预先训练了这些网络，这样一来就可以使用这些网络进行迁移学习。

9 迁移学习（Transfer Learning）

如果要做一个计算机视觉的应用，相比于从头训练权重，或者说从随机初始化权重开始，如果能够下载别人已经训练好的网络结构的权重，用别人训练好的参数作为预训练，然后转换到自己的任务上，那将会节约很多时间。计算机视觉的研究社区非常喜欢把许多数据集上传到网上，比如ImageNet，或者MS COCO，或者Pascal类型的数据集，这些都是不同数据集的名字，它们都是由大家上传到网络的，并且有大量的计算机视觉研究者已经用这些数据集训练过他们的算法了。有时候这些训练过程需要花费好几周，并且需要很多的GPU。其它人已经做过了，并且经历了非常痛苦的寻最优过程，这就意味着可以下载花费了别人好几周甚至几个月而做出来的开源的权重参数，把它当作一个很好的初始化用在自己的神经网络上。下面具体说明如何用迁移学习把公共的数据集的知识迁移到自己的问题上。

举个例子，假如说要建立一个猫咪检测器，用来检测自己的宠物猫。比如网络上的Tigger，是一个常见的猫的名字，Misty也是比较常见的猫名字。假如有两只猫叫Tigger和Misty，还有一种情况是，两者都不是。所以现在有一个三分类问题，图片里是Tigger还是Misty，或者都不是（忽略两只猫同时出现在一张图片里的情况）。现在可能没有大量Tigger或者Misty的图片，所以训练集会很小。

现可以从网上下载一些神经网络开源的实现，不仅把代码下载下来，也把权重下载下来。举个例子，ImageNet数据集，它有1000个不同的类别，因此这个网络会有一个Softmax单元，它可以输出1000个可能类别之一。

可以去掉这个Softmax层，创建自己的Softmax单元，用来输出Tigger、Misty和neither三个类别。就网络而言，建议把所有的层看作是冻结的，冻结网络中所有层的参数，只需要训练和自己的Softmax层有关的参数。这个Softmax层有三种可能的输出，Tigger、Misty或者都不是。

通过使用其他人预训练的权重，即使只有一个小的数据集，也很可能得到很好的性能。幸运的是，大多数深度学习框架都支持这种操作，事实上，取决于用的框架，它也许会有trainableParameter=0这样的参数，对于这些前面的层，可能会设置这个参数。为了不训练这些权重，有时也会有freeze=1这样的参数。不同的深度学习编程框架有不同的方式，允许指定是否训练特定层的权重。在这个例子中，只需要训练softmax层的权重，把前面这些层的权重都冻结。

另一个技巧，也许对一些情况有用，由于前面的层都冻结了，相当于一个固定的函数，不需要改变。因为不需要改变它，也不训练它，取输入图像，然后把它映射到这层（softmax的前一层）的激活函数。所以这个能加速训练的技巧就是，如果先计算这一层（紫色箭头标记），计算特征或者激活值，然后把它们存到硬盘里。现在需要做的就是用这个固定的函数，在这个神经网络的前半部分（softmax层之前的所有层视为一个固定映射），取任意输入图像，然后计算它的某个特征向量，这样所训练的就是一个很浅的softmax模型，用这个特征向量来做预测。对现在计算有用的一步就是对训练集中所有样本的这一层的激活值进行预计算，然后存储到硬盘里，然后在此之上训练softmax分类器。所以，存储到硬盘或者说预计算方法的优点就是不需要每次遍历训练集再重新计算这个激活值了。

因此如果任务只有一个很小的数据集，可以冻结softmax层之前的所有层。如果现在有一个较大的训练集，就应该冻结更少的层，比如只把下图最右边的两层冻结，然后训练后面的层。如果输出层与模板的类别不同，那么需要构建自己的输出单元。比如可以取后面几层的权重，用作初始化，然后开始梯度下降。

或者可以直接去掉后面这几层，换成自己的隐藏单元和softmax输出层，这些方法值得一试。但是有一个规律，如果有越来越多的数据，需要冻结的层数越少，能够训练的层数就越多。这个理念就是，如果有一个更大的数据集，那么不要单单训练一个softmax单元，而是考虑训练中等大小的网络，包含最终要用的网络的后面几层。

最后，如果有大量数据，应该做的就是用开源的网络和它的权重，把这所有的权重当作初始化，然后训练整个网络。极端情况下，可以用下载的权重只作为初始化，用它们来代替随机初始化，接着可以用梯度下降训练，更新网络所有层的所有权重。

以上就是卷积网络训练中的迁移学习。事实上，网上的公开数据集非常庞大，对于很多计算机视觉的应用，如果下载其他人的开源的权重，并用作自己问题的初始化，效果会更好。除非有一个极其大的数据集和非常大的计算量预算来从头训练网络，否则迁移学习是非常值得考虑的。

10 数据增强（Data augmentation）

大部分的计算机视觉任务需要使用很多的数据，所以数据扩充是经常使用的一种技巧。计算机视觉是一个相当复杂的工作——需要输入图像的像素值，然后弄清楚图片中有什么，似乎需要学习一个复杂方程来做这件事。在实践中，更多的数据对大多数计算机视觉任务都有所帮助，不像其他领域，有时候得到充足的数据，但是效果并不怎么样。但是，当下在计算机视觉方面，计算机视觉的主要问题是没有办法得到充足的数据。对大多数机器学习应用，这不是问题，但是对计算机视觉，数据就远远不够。所以这就意味着当训练计算机视觉模型的时候，数据扩充会有所帮助，这是可行的，无论是使用迁移学习从别人的预训练模型开始，或者从源代码开始训练模型。下面介绍一些计算机视觉中常见的数据扩充的方法。

最简单的数据扩充方法或许是垂直镜像对称。假如，训练集中有一张上图所示的图片，然后将其翻转得到右边的图像。对大多数计算机视觉任务，左边的图片镜像对称后仍然是猫，如果镜像操作能够保留了图像中想识别的物体，那他将是个很实用的数据扩充技巧。

另一个经常使用的技巧是随机裁剪，给定一个数据集，然后开始随机裁剪，可以得到不同的图片。随机裁剪并不是一个完美的数据扩充的方法，如果随机裁剪的那一部分（红色方框标记部分，编号4），这部分看起来不像猫。但在实践中，这个方法还是很实用的，随机裁剪构成了很大一部分的真实图片。

镜像对称和随机裁剪是经常被使用的两种方法。当然，理论上，也可以使用旋转，剪切（shearing：此处并非裁剪的含义，图像仅水平或垂直坐标发生变化）图像，可以对图像进行扭曲变形，引入局部弯曲等等。在实践中，这些方法因为太复杂了所以使用的很少。

第三种经常使用的方法是彩色转换，对一张图片的R、G和B三个通道上加上不同的失真值。

上图编号1中的图片是给红色、蓝色通道加值，给绿色通道减值。红色和蓝色会产生紫色，使整张图片看起来偏紫；在第二个例子中（编号2），少用了一点红色，用了更多的绿色和蓝色色调，这就使得图片偏黄一点；在第三个例子中（编号3）使用了更多的蓝色，仅仅多了点红色。这样训练集中就有了失真的图片。

这里对图片的颜色进行改变比较夸张，而在实践中，R、G和B的值是根据某种概率分布来决定的，其改变可能会很小。

改变色彩除了能够扩充数据集外这个原因外，还有一个原因就是图像的颜色会受到阳光、灯光照明等外部条件的影响，这些因素对图片内容的识别结果会产生干扰，因此采用颜色失真的方法，会使得学习算法对照片的颜色更改更具鲁棒性。

正如前文所说，对R、G和B有不同的采样方式，其中一种影响颜色失真的算法是PCA颜色增强，即主成分分析。PCA颜色增强的大概含义是如果图片呈现紫色，即主要含有红色和蓝色，绿色很少，然后PCA颜色增强算法就会对红色和蓝色增减很多，绿色变化相对少一点，所以使总体的颜色保持一致。如果不懂PCA技术，好在能够方便地找到PCA颜色增强的开源实现方法，然后直接使用它。

存储好的训练数据通常存在硬盘上，使用圆桶来表示硬盘。计算机通过CPU线程不停的从硬盘中读取图片数据，因此通常可以使用CPU线程来实现上述的失真变形——可以是随机裁剪、颜色变化，或者是镜像。对每张图片得到对应的某一种变形失真形式，对其进行镜像变换可以得到编号1的图片，对其使用颜色失真，这张图最后会发生颜色变化（编号2）。

与此同时，CPU线程持续加载数据，然后实现任意失真变形，从而构成批数据或者最小批数据，这些数据持续的传输给其他线程或者其他的进程，然后开始训练，可以在CPU或者GPU上实现训一个大型网络的训练。

常用的实现数据扩充的方法是使用一个线程或者是多线程，这些可以用来加载数据，实现变形失真，然后传给其他的线程或者其他进程，来训练不同的图片。

11 计算机视觉现状（The state of computer vision）

深度学习已经成功地应用于计算机视觉、自然语言处理、语音识别、在线广告、物流还有其他许多问题。在计算机视觉的现状下，计算机视觉领域的深度学习应用有一些独特之处。

大部分机器学习问题是介于少量数据和大量数据范围之间的。举个例子，相对于图像识别这个问题的复杂性而言，可以认为语音识别领域有相当数量的识别数据；虽然现在图像识别或图像分类方面也有大量数据集，但是图像识别是一个复杂的问题，即使在线数据集非常大，如超过一百万张图片，大家仍然希望能有更多的数据。还有一些问题，比如物体检测，拥有的数据更少。提醒一下，图像识别其实是判断图片里是否存在某一物体，比如判断图片里是不是有一只猫；对象检测则是看一幅图，然后判断这幅图片里面物体是什么，比如汽车等等。因为获取边框的成本比标记对象的成本更高，所以进行对象检测的数据往往比图像识别数据要少。 

所以，当有很多数据时，人们倾向于使用更简单的算法和更少的手工工程，因为不需要为这个问题精心设计特征。当有大量的数据时，只要有一个大型的神经网络，甚至一个更简单的架构，可以是一个神经网络，就可以去学习它想学习的东西。 

相反当没有那么多的数据时，人们从事更多的是手工工程，低调点说就是有很多小技巧可用（在机器学习或者深度学习中，一般更崇尚更少的人工处理，而手工工程更多依赖人工处理）。

学习算法有两种知识来源，一个来源是被标记的数据；第二个知识来源是手工工程。有很多方法去建立一个手工工程系统，它可以是源于精心设计的特征，手工精心设计的网络体系结构或者是系统的其他组件。当没有太多标签数据时，只需要更多地考虑手工工程。

所以计算机视觉是在试图学习一个非常复杂的功能，经常感觉没有足够的数据，即使获得了更多数据，还是经常觉得还是没有足够的数据来满足需求。这就是为什么计算机视觉，从过去甚至到现在都更多地依赖于手工工程——这也是计算机视觉领域发展相当复杂网络架构的原因，在缺乏更多数据的情况下，获得良好表现的方式还是花更多时间进行架构设计，或者说在网络架构设计上花费（更多时间。

幸运的是，当只有少量的数据时，还有迁移学习。迁移学习会有很大帮助，有相对较少的数据时就可以产生很多相似的数据。

下面是一些有助于在基准测试中表现出色的小技巧。（整理者注：Benchmark 基准测试，Benchmark是一个评价方式，在计算机领域应用最成功的就是性能测试，主要测试负载的执行时间、传输速度、吞吐量、资源占用率等。）

其中一个是集成。在确定了自己的神经网络之后，可以独立训练几个神经网络，并平均它们的输出。比如说随机初始化三个、五个或者七个神经网络，然后训练所有这些网络，然后平均它们的输出。另外对他们的输出进行平均计算是很重要的，不要平均他们的权重，这是行不通的。对7个神经网络，它们有7个不同的预测，然后平均他们，这可能会使得预测在基准上提高1%，2%或者更好。7个神经网络意味着一张图片需要被运算7次，这可能会让运行时间变慢。

对基准测试有帮助的另一个技巧就是Multi-crop at test time，它是一种将数据扩充应用到测试图像中的一种形式。

举个例子，然后把一张猫的图片复制四遍，再将它的镜像版本也复制四遍，最终得到10张图片。再使用一种叫作10-crop的技术（crop理解为裁剪的意思）：取图片的中心区域进行裁剪裁剪，然后通过分类器去运行它；然后取左上角区域，运行分类器；右上角用绿色表示；左下方用黄色表示；右下方用橙色表示，统统通过分类器来运行它；然后对镜像图像做同样的事情。

编号1和编号3就是中心crop，编号2和编号4是四个角落的crop。如果把这些加起来，就会有10种不同的图像的crop，因此将这种multi-crop技术命名为10-crop。所以要做的就是，通过分类器来运行这十张图片，然后对结果进行平均。如果有足够的计算预算，当然可以这么做，甚至可以使用更多crop，这可能会获得更好的性能。

集成的一个大问题是需要保持所有这些不同的神经网络，这就占用了更多的计算机内存。对于multi-crop，只保留一个网络，所以它不会占用太多的内存，但它仍然会让运行时间变慢。

这些小技巧在基准测试和竞赛上做得很好，研究论文也可以参考这些，但在构建生产系统时并不推荐使用这些方法。

由于计算机视觉问题建立在小数据集之上，其他人已经完成了大量的网络架构的手工工程。一个神经网络在某个计算机视觉问题上很有效，它通常也会解决其他计算机视觉问题。所以，要想建立一个实用的系统，最好先从其他人的神经网络架构入手。如果可能的话，可以使用开源的一些应用，因为开放的源码实现可能已经找到了所有繁琐的细节，比如学习率衰减方式或者超参数。最后，其他人可能已经在几个GPU上花了几个星期的时间来训练一个模型，训练了超过一百万张图片，所以通过使用其他人预先训练得到的模型，然后在数据集上进行微调，就可以在应用程序上运行得更快。

12 后记

本文是对吴恩达的深度学习教程的文字总结，其文字以及图片主要来自于视频以及笔记。在学习了视频教程内容后，基于课程笔记的内容以及自己对卷积神经网络的理解，最终成此文。相比于笔记原文档，本文基本没有改变原文档的内容与布局，只对文中极少部分内容进行了微调。

此外，如果需要吴恩达卷积神经网络教程的PDF课件，可以参见参考文献的连接。