主成分分析(PCA)及其MATLAB的实现方法
出处:
作者:远方的路很长
链接:https://zhuanlan.zhihu.com/p/501353361
概述
PCA的目的
PCA的几何意义
原理与步骤简述
算法一:特征分解(Eigen Decomposition)
算法二:奇异值分解(Singular Value Decomposition,SVD)
r rr的选取标准
两种算法的比较
MATLAB的实现方法
特征分解法:利用`eig`函数
SVD法:利用`svd`函数
利用`pca`函数
应用
聚类分析
图像压缩
人脸检测与匹配
1概述
2PCA的目的
假设现在有这样一个情景:现在要统计并可视化分析男大学生体测成绩,如果只参考立定跳远和1000m成绩两项指标,我们可以以立定跳远成绩作为x xx轴,1000m成绩作为y yy轴做出散点图,每个点代表一个学生;若统计三项指标,我们也可以在三维空间中做出散点图;但如果要统计四项乃至更多的指标,我们就无法再以此方法进行数据的可视化。
而主成分分析(Principal Component Analysis,PCA)的方法,可以将具有多个观测变量的高维数据集降维,使人们可以从事物之间错综复杂的关系中找出一些主要的方面,从而能更加有效地利用大量统计数据进行定量分析,并可以更好地进行可视化、回归等后续处理。
3PCA的几何意义
即
式中W \boldsymbol WW为旋转变换矩阵,有如下性质:
也就是说,PCA并不会对原有数据做任何的改变,而只是将“观看”原有数据的视角转换了,即,在原有数据空间中的数据的相对位置,与在主成分空间(Principal Component Space)中的相对位置是完全相同的,相当于只是更换了原有数据的基底。
4原理与步骤简述
算法一:特征分解(Eigen Decomposition)
1.先对A 进行中心化(整体平移数据,使数据中心在( 0 , 0 ) :
5两种算法的比较
6MATLAB的实现方法
我们先载入MATLAB自带的数据集fisheriris(该数据集统计了三种鸢尾花的花萼长、花萼宽、花瓣长、花瓣宽),然后进行中心化处理,并计算协方差矩阵:
load fisheriris;
X = meas; % n = 150, m = 4
% 中心化
meanX = ones(size(X,1), 1) * mean(X);
centredX = X - meanX;
C = cov(centredX); % 直接调用cov直接计算协方差矩阵即可
征分解法:利用eig函数
[W, Lambda] = eig(C); % W是特征向量组成的矩阵(4×4),Lambda是特征值组成的对角矩阵
ev = (diag(Lambda))'; % 提取特征值
ev = ev(:, end:-1:1); % eig计算出的特征值是升序的,这里手动倒序(W同理)
W = W(:, end:-1:1);
sum(W.*W, 1) % 可以验证每个特征向量各元素的平方和均为1
Wr = W(:, 1:2); % 提取前两个主成分的特征向量
Tr = centredX * Wr; % 新坐标空间的数据点
% 作图
figure;
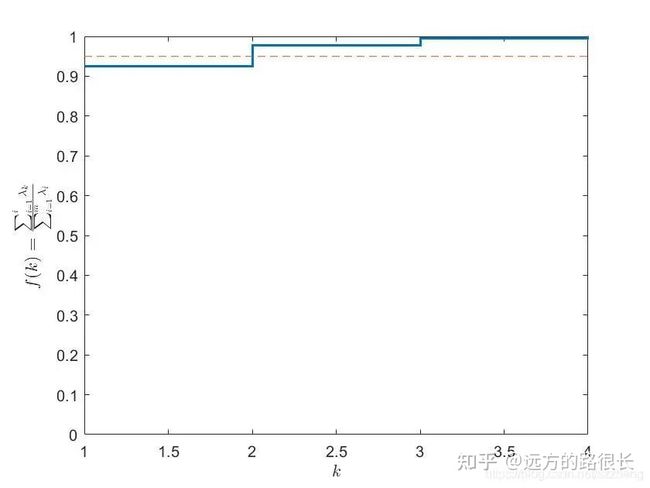
stairs(cumsum(ev)/sum(ev), 'LineWidth',1.5);
axis([1 4 0 1]);
xlabel('kk', 'Interpreter', 'latex');
ylabel('f(k)=∑ii=1λk∑mi=1λif(k)=∑i=1iλk∑i=1mλi',...
'Interpreter', 'latex');
hold on;
plot([1 4], [0.95 0.95], '--'); % 从图中可以看出,取r = 2即可
figure;
scatter(Tr(:,1), Tr(:,2), 130, categorical(species), '.');
colormap(winter);
xlabel('Principal Component 1');
ylabel('Principal Component 2');
SVD法:利用svd函数
[U, Sigma, V] = svd(X); % 可以检验,W和V完全相同(向量的正负号不影响)
Vr = V(:, 1:2); % 提取前两个主成分的特征向量
Tr = X * Vr; % 新坐标空间的数据点
% 画图部分同上,略
利用pca函数
pca的常用调用格式如下:
[loadings, scores] = pca(X, 'NumComponents', r);
其中:
[Wr, Tr, ev] = pca(X, 'NumComponents',2);
% 画图部分略
应用
聚类分析
例如,我们在电商平台浏览并购买商品时,平台就会收集你的年龄、性别、购买商品平均价格、购买频率、最初浏览商品直到最终购买之间的时间间隔等等大量、多维度的信息,然后进行降维,将你归于“大学生”“白领”“一家三口”等类别,然后定向为你推送促销商品的通知。