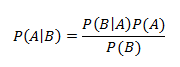李宏毅深度学习自用笔记(未完)
文章目录
-
- 1.机器学习是干什么的?
- 1.机器学习能够找到那些函数?
- 1.如何告诉机器我们希望找到什么函数?
- 1.机器如何找到我们想要的函数?
- 1.机器学习的三个步骤:
- 2.线性回归模型
- 2.梯度下降
- 2.如何选择模型、减小误差
- 2.欠拟合
- 2.过拟合
- 2.平滑
- 2.正则化
- 2.交叉验证
- 3.梯度下降再回顾
- 3.自适应学习率
- 3.Adagrad
- 4.分类模型
- 4.为什么不能把分类当成回归去做?
- 4.理想的替代方案
- 4.贝叶斯公式
- 4.全概率公式
- 4.似然函数
- 4.概率生成模型
- 4.Sigmoid函数
- 4分类模型之逻辑回归
- 4.逻辑回归与线性回归比较
- 4.为什么逻辑回归模型中不使用Square Error
- 4.判别模型VS生成模型
- 4.多分类
-
- Softmax
- 损失函数
- 梯度
- 4.逻辑回归的局限
- 4.特征变换
- 4.神经网络(Neural Network)
- 5.深度学习
-
- 深度学习的三个步骤
- 神经网络的结构
- 全连接前馈神经网络
- 一些网络
- 机器学习和深度学习的工作重点
- 关于深度学习的一些疑问
- 5.神经网络为什么要是深度的
- 5.神经网络中的反向传播算法
- 6.神经网络训练问题与解决方案
-
- 明确问题类型及其对应方法
- 处理神经网络在训练集上性能不好的情况的方法
- 处理神经网络在测试集上性能不好的情况的方法
- 一些性能优化方法的简介
- 6.神经网络精度低不一定是因为过拟合
- 6.梯度消失
- 6.ReLU等其他常用的激活函数
-
- ReLU(Rectified Linear Unit)
- Leaky ReLU
- Parametric ReLU
- Maxout
- 6.学习率调整方法
-
- RMSProp
- Momentum
- Adam
- Adam VS SGDM
- SWATS
- 尝试改进Adam
- 尝试改进SGDM
- 改进Momentum
- Early Stopping
- 6.如何提高神经网络的鲁棒性
-
- 正则化
- Dropout
- 6.On-line VS Off-line
- 7.CNN卷积神经网络
-
- **识别图像时的一些特点**
- CNN架构
- CNN架构作用探析
- **卷积(Convolution)**
- **最大池化(Max Pooling)**
- **Flatten**
- CNN到底学到了什么?
-
- 卷积层学到了什么?
- 全连接层学到了什么?
- 输出层学到了什么?
- 7.CNN应用案例
- 7.CNN应用案例
1.机器学习是干什么的?
机器学习是要让机器找到一个函数,类似于语音识别(输入语音输出文字)、图像分类(输入图片,输出类别)、AlphaGO下围棋(输入棋盘状态输出下一步落棋位置)这样的函数。
1.机器学习能够找到那些函数?
运用最多的是两大类函数:回归和分类。
回归(Regression):输出是一个连续的数值、标量。我的理解就是根据以往的数据对未知的一个预测。
应用:比如PM2.5的预测。
分类(Classification):输出是一个离散的值。
应用:二分类(Binary Classification),输出是0或1、Yes或No、正面或负面(情感分析)。
多分类(Multi-Category Classification),输出是[1,2,3,…,N],比如图像分类(猫?狗?还是其他的啥。)
事实上除了回归和分类还有一类,生成(Generation)。生成是指让机器学习如何创造,比如生成文本、图片等。
1.如何告诉机器我们希望找到什么函数?
怎么为机器提供学习资料呢?
着重介绍 有监督学习(Supervised Learning)和强化学习(Reinforcement Learning)。
首先,特征是指一个事物原有的属性,标签(Label)是指根据固有属性产生的认知或是结论。
有监督学习:“监督”即为“标签”,也就是说数据集中不仅包括特征还包括标签。有了标签,我们就可以评价一个函数的好坏,进而优化这个函数。使用Loss判断函数的好坏,Loss越小,函数越好。以机器学习下围棋为例,有监督学习函数的输入(数据特征)就是棋盘状态,函数的输出(数据标签)就是下一步落棋的位置。
Tips:Loss/评价指标是多样的、优化方法也是多样的。
强化学习:以机器学习下围棋为例,强化学习就是让机器和自己或和别人下棋,把输或赢的结果作为Reward,引导机器学习如何下棋。
如果它赢了,那么它就知道这一盘里有几步棋下的好,但不知道具体是哪几步;输了亦然。
**有监督学习和强化学习的比较:**有监督学习不仅把训练数据丢给计算机,还把分类的结果(数据标签)丢给计算机分析,这样机器在学习时不仅有训练数据,还有训练结果(标签)。训练结束后进行测试。==相当于把题目给了机器,还把参考答案给了机器。==理论上,强化学习不通过人类给出的标签去学习,可能学习出更强大的实力。
原始的AlphaGO是先通过有监督学习到一定程度,之后再用强化学习继续优化。新版本的AlphaGO则是完全通过强化学习实现的,且优于原始的AlphaGo。
无监督学习:只给机器提供数据特征,不提供数据标签。只给你题目自己练习,不给参考答案
1.机器如何找到我们想要的函数?
首先我们给定函数的形式以及范围,这就是模型,模型就是一个函数集。(比如假定我们要得到的函数是线性模型、神经网络等等。)
然后我们确定这个模型的各项参数,这就得到了函数。
找到更好的函数:使用梯度下降(Gradient Descent),找到更好的函数。
1.机器学习的三个步骤:
1.确定模型/函数集
2.确定如何评价函数的好坏
3.确定如何找到最好的函数
2.线性回归模型
**应用案例:**股票预测、自动驾驶预测方向盘转动角度、推荐系统预测某用户购买某商品的可能性。
线性回归模型(Linear Regression Model):
如 y = f ( x ) = w ⋅ x + b y=f(x)=w\cdot x+b y=f(x)=w⋅x+b
-
y y y是输出;
y ^ \hat y y^是真实值/标签(label)
-
w w w是权重(weight);
-
b b b是偏置(bias);
-
x x x是输入(input),也可叫做特征(feature)
数据集中一般包含多个object,每个object一般包含多个component。此时,上标是object的索引,下标是component的索引。
-
损失函数(Loss Function)
如果不考虑模型的好坏,衡量一个函数的好坏,其实是衡量模型参数的好坏。
以线性模型为例,就是衡量参数 w w w和 b b b的好坏。如下,把所有样本误差的平方和作为损失函数
L ( f ) = L ( w , b ) = ∑ n = 1 10 ( y ^ − ( b + w ⋅ x n ) ) 2 L(f)=L(w,b)=\sum_{n=1}^{10}(\hat y-(b+w\cdot x^n))^2 L(f)=L(w,b)=n=1∑10(y^−(b+w⋅xn))2
损失函数越大,则这个函数越差,与数据集中内容越不相符。
2.梯度下降
原理很简单。首先梯度下降的目的是优化损失函数的值,使其尽量小,也就是找到最好的模型参数(在数据集上拟合效果最好)。
下面举个例子,假设模型 f f f 中只有一个参数 w w w,损失函数为 L ( f ) = L ( w ) L(f)=L(w) L(f)=L(w),(若模型中有多个函数,按相同方法更新各个参数)
1.在损失函数上选择一个点。
2.计算该点损失函数 L ( f ) L(f) L(f)对该参数 w w w的导数(梯度)。显然,如果导数小于0则 L ( f ) L(f) L(f)会随着 w w w的增大而减小,反之亦然。
3.更新参数模型:
w 1 = w 0 − l r d L ( f ) d w ∣ w = w 0 w^1=w^0-lr\frac{dL(f)}{dw}|_{w=w^0} w1=w0−lrdwdL(f)∣w=w0
w w w的变化量取决于梯度和学习率(Learning Rate)的大小:梯度绝对值或学习率越大,则 w w w变化量越大。
4.重复第2步和第3步
经过多次参数更新/迭代(iteration),可以使损失函数的值达到局部最小(即局部最优,Local Optimal),但不一定是全局最优。
特别地,如果模型有多个参数则计算损失函数在各个参数方向上的偏导数。后面根据偏导数对应更新各参数。
2.如何选择模型、减小误差
首先,模型越复杂一般在训练集上的误差就越小。但是复杂的模型在测试集上的误差不一定小,因为模型过于复杂时,就很容易受到数据的影响,可能导致过拟合。
**误差(error)**来源于两个方面,一是Bias,二是Variance。权衡(trade-off)两者才能使总误差最小。
如果把机器学习得到的函数称作人工函数,把理想中的最佳函数称作“上帝函数”。那么Bias就是人工函数和上帝函数两者之间的差距。
而Variance则是人工函数的离散程度(相同模型在不同数据上拟合得到不同函数)。如图:
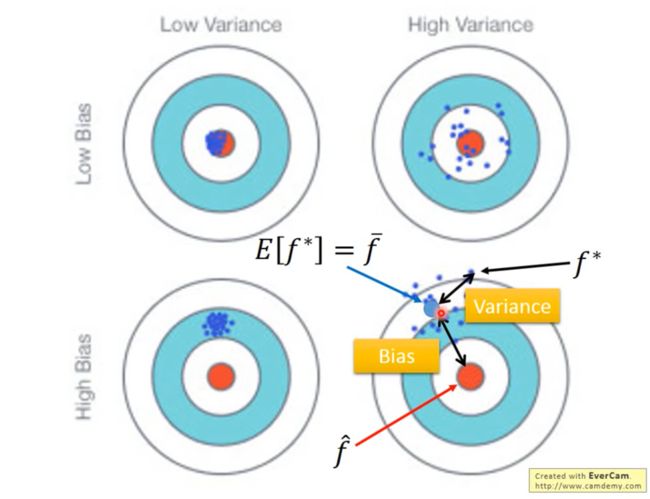
一般来说,模型越复杂,Bias越小,Variance越大。也就是说复杂的模型可能距离上帝函数很近,但是很松散。
如图,横轴是模型的最高次幂数(复杂程度),纵轴是误差大小:

直观的解释什么是Variance就是,相同模型在不同数据上拟合得到的不同函数,而这些函数之间的离散程度就是Variance。
如图:
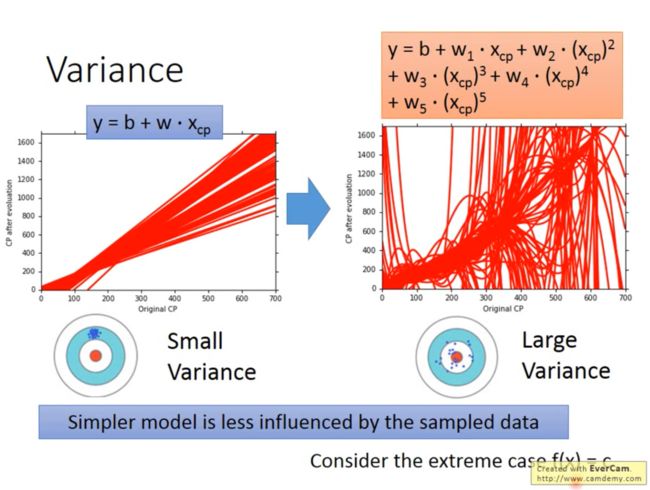
那么为何模型越复杂Variance越大呢?因为模型越简单就越不容易被数据影响,也就是对数据不敏感。也就会使得同一个模型在不同的数据条件下得到的函数依然很接近。反之模型过于复杂则会过于受数据影响。还有一个说法是,过于复杂的模型在测试集上能得到较好的效果是因为模型过于“讨好”训练集,所以对于不同的数据样本即测试集往往会表现出不好的效果。
直观的解释什么是Bias就是相同的模型在不同的数据上拟合得到不同的函数,这些函数的“期望”与“真理”的差距就是Bias。
那么为何模型越简单Bias越大呢?,因为模型就是个函数集(Function Set),模型越简单,则包含的函数就越少,包含上帝函数的概率就越小,甚至可能不保函上帝函数,在函数集很小的情况下,即使是其中最好的函数,还是与上帝函数相差很大。
如图:

2.欠拟合
如果模型在训练集上的误差就很大了,那就是欠拟合,一般是模型太简单。此时显然Bias是大的,由于模型较简单所以受数据影响较小,因此Variance较小。
**怎样应对Bias过大的情况呢?**这个时候需要更复杂的模型。(考虑添加更多维度的输入、把线性模型换成非线性模型等等)
2.过拟合
如果模型在训练集上的误差很小,在测试集上的误差很大,此为过拟合。此时Variance是大的,而Bias较小。
**怎样应对Variance较大的情况?**1.使用更复杂的数据集(很难做到) 2.使用更简单的模型(不是根本方法) 3.正则化
2.平滑
平滑是指输出受输入影响的程度。输出越受输入影响,则越不平滑。函数的参数越接近0则函数越平滑。
输入往往包含一些干扰/噪音(noise),当函数非常的不平滑时,输出会受这些干扰的影响很大。
但当函数过于平滑时,极端的想,输出完全不受输入影响,显然这也是不行的。
所以 ,我们追求适度的平滑。
2.正则化
如图所示,过于平滑的曲线在训练集上的表现都不行,在测试集上的表现更不用说,这是欠拟合。而非常不平滑的曲线,过于“迁就”训练集数据,几乎每一个训练集上的数据点都完美通过曲线,这种曲线在测试集上的表现往往很差,不具有很好的“预测”性能。我们希望一个适当平滑的曲线,如中间曲线所示,这个曲线在测试集上的表现性能最佳。
损失函数:
L ( f ) = L ( w , b ) = ∑ n = 1 10 ( y ^ − ( b + w ⋅ x n ) ) 2 L(f)=L(w,b)=\sum_{n=1}^{10}(\hat y-(b+w\cdot x^n))^2 L(f)=L(w,b)=n=1∑10(y^−(b+w⋅xn))2
拟合的过程就是让损失函数尽量地小,也就是让 b + w ⋅ x n b+w\cdot x^n b+w⋅xn 和 y ^ \hat y y^ 尽量相等。这能保证我们的模型在训练集上有很好的表现,但是并不一定能保证在测试集上同样有很好的表现,训练集上表现好测试集上表现差的情况就叫做过拟合。事实上,我们更重视模型在测试集上的表现。
如何让曲线平滑呢?应该让参数尽量接近0,特别是高次项参数尽量接近0,这样就会一定程度上降低输入数据对输出的影响。想想看,当参数很大时,输入数据一个微小的差距都会使输出结果呈现很大的差距,显然是不平滑的。 所以我们这样做:
用 L n e w = L o l d + λ ∑ ( w i ) 2 L_{new}=L_{old}+\lambda \sum(w_i)^2 Lnew=Lold+λ∑(wi)2 取代原有的损失函数。新的损失函数有什么好处呢?当我们想让损失函数的值足够的小不仅要考虑 L o l d L_{old} Lold足够接近0,还要兼顾 λ ∑ ( w i ) 2 \lambda \sum(w_i)^2 λ∑(wi)2 足够接近0。这就要求参数不能太大。其中 $\lambda $ 是一个常数,需要手动尝试选取最好的。
2.交叉验证
可以这样理解,训练一个模型我们需要一部分数据做训练集,一部分训练做测试集,这就是交叉验证。
具体来说,常用的交叉验证方法有这些:
The Validation Set Approach、LOOCV(Leave One Out Cross Validotion)、K折交叉验证(K-fold Cross Validation)
The Validation Set Approach:将数据集的一部分用作训练集,一部分用作测试集。
缺点:你需要找到合理的划分方法,并且你将只能把其中的一部分用作训练。
LOOCV(Leave One Out Cross Validotion):假设有N个数据,把其中的一个数据挑出来当成测试集,其余的N-1个数据作为训练集。每一次都挑选一个不同的数据做测试集,直到把这个过程重复N次。这样我们将得到N个模型与N个误差值,我们用这N个误差值的平均值来评估这个模型。
优点是几乎利用了所有的数据作为训练集,保证了模型的Bias更小。缺点是运算量很大。
K折交叉验证(K-fold Cross Validation):事实上是LOOCV方法的折中,把数据集分成K份,把其中的一份作为测试集,其他的K-1份作为训练集,把这个过程重复K次。这样我们将得到K个模型以及K个误差值,用K个误差值的平均数来评估这个模型。
K的选取是Bias和Variance的trade-off。一般选择10。
K越大,训练集就越大,Bias就越小。但是当K过于大时,Variance也会太大。
3.梯度下降再回顾
首先我们假设模型只有一个参数 w w w,也就是损失函数 L ( f ) = L ( w ) L(f)=L(w) L(f)=L(w),梯度下降算法如下。(如果有多个参数,同理)
1.初始化参数:选取一个点 w 0 w^0 w0,令 w = w 0 w=w^0 w=w0。
2.计算梯度: d L ( f ) d w ∣ w = w 0 \frac{dL(f)}{dw}|_{w=w^0} dwdL(f)∣w=w0
3.更新参数: w 1 = w 0 − l r d L ( f ) d w ∣ w = w 0 w^1=w^0-lr\frac{dL(f)}{dw}|_{w=w^0} w1=w0−lrdwdL(f)∣w=w0
4.重复第2步和第3步:经过多次参数更新/迭代,使损失函数的值达到局部最优。(但不一定是全局最优)
3.自适应学习率
(Adaptive Learning Rate)
在梯度下降过程中,学习率 l r lr lr是固定的,这不合理。因为,有时候学习率过大会导致loss不降反升,甚至跳过最小点;而如果学习率过低,则会导致整个梯度下降过程很慢。我们应该有个方法让每个参数都有各自的学习率。
基本思路是随着参数迭代更新的进行,学习率逐渐降低。比如说: η t = η t + 1 \eta^{t}=\frac{\eta}{\sqrt{t+1}} ηt=t+1η, t t t代表迭代次数,这个式子实现了随着迭代次数的增加学习率逐渐降低,但是还是太简陋。Adagrad是个很好的方法。
3.Adagrad
Adagrad (Adaptive Gradient Descent),自适应梯度下降。核心是每个参数都有不同的学习率。
Adagrad的梯度下降是这样更新参数的:
w t + 1 = w t − η ∑ i = 0 t ( g i ) 2 g t w^{t+1}=w^t-\frac{\eta}{\sqrt{\sum_{i=0}^t(g^i)^2}}g^t wt+1=wt−∑i=0t(gi)2ηgt
其中 η \eta η是初始学习率, g t g^t gt 是该点的梯度。
怎么得到这个式子的呢?
式子的模型是这样的: w t + 1 = w t − η t σ t g t w^{t+1}=w^t-\frac{\eta^t}{\sigma^t}g^t wt+1=wt−σtηtgt (式子1)
其中 η t = η t + 1 \eta^t=\frac{\eta}{\sqrt{t+1}} ηt=t+1η,也就是学习率基于时间变小。
而 σ t = 1 t + 1 ∑ i = 0 t ( g i ) 2 \sigma^t=\sqrt{\frac{1}{t+1}\sum_{i=0}^t(g^i)^2} σt=t+11∑i=0t(gi)2是前面所有梯度的均方根。(均方根:平方、平均、开方)
代入式子1,可以消掉 t + 1 t+1 t+1就得到 w t + 1 = w t − η ∑ i = 0 t ( g i ) 2 g t w^{t+1}=w^t-\frac{\eta}{\sqrt{\sum_{i=0}^t(g^i)^2}}g^t wt+1=wt−∑i=0t(gi)2ηgt
其中 g t g^t gt 是该点的梯度。
这样一来,随着迭代次数越来越多, t t t越来越大,学习率就越来越小。
4.分类模型
应用案例:
信用评分(芝麻分等):输入:收入、储蓄、职业、年龄、信用历史等。
输出:是否给你放款。
医疗诊断:输入:目前症状、年龄、性别、病史。
输出:哪种疾病。
手写文字识别:输入:文字图片
输出:是哪一个汉字
人脸识别:输入:面部图片
输出:是哪个人
4.为什么不能把分类当成回归去做?
假设我们去分类两个类别,类别1的标签是-1,类别2的标签是1,那么0就是分界线,小于0就是类别1,大于0就是类别2。由于回归模型会惩罚那些很极端的样本事实上,这类值在分类模型中代表着置信度很高,如果某些输出远远大于1,这时回归函数会被这些很极端的值“带偏”(如下图),就会导致一些分界线附近的值不准确。
假设有多个类别,类别1的标签是1,类别2的标签是2,类别3的标签是3。回归模型会认为存在3大于2之类的关系,这在分类中是说不通的。
4.理想的替代方案
模型:根据特征判断类别
输入:特征
输出:类别
损失函数: L ( f ) = ∑ n δ ( f ( x n ) ≠ y ^ n ) L(f)=\sum_n\delta(f(x^n)\neq\hat y^n) L(f)=∑nδ(f(xn)=y^n)
也就是预测错误的次数。
如何找到最好的函数:比如感知机(Perceptron)、支持向量机(SVM)
4.贝叶斯公式
P ( A ∩ B ) = P ( A ) P ( B ∣ A ) = P ( B ) P ( A ∣ B ) P(A\cap B)=P(A)P(B|A)=P(B)P(A|B) P(A∩B)=P(A)P(B∣A)=P(B)P(A∣B)
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) P(A|B)=\frac{P(B|A)P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)P(A)
贝叶斯公式是用来计算后验概率的。后验概率也就是已知某种结果,求解导致这种结果的第i种原因的可能性是多少。(有果推因)
举个例子:假设导致我们上班堵车的因素有2个,一个是天气另一个是交通事故。某一天遭遇堵车,我们计算由交通事故引起的概率有多大,这就叫做后验概率。(也叫条件概率)
Bayes公式_肖潇不吃洋芋的博客-CSDN博客_贝叶斯公式
先验概率、后验概率和似然函数的区别和联系_lfeifan的博客-CSDN博客_似然函数和后验概率
4.全概率公式
P ( B ) = ∑ i = 1 n P ( A i ) P ( B ∣ A i ) P(B)=\sum_{i=1}^nP(A_i)P(B|A_i) P(B)=∑i=1nP(Ai)P(B∣Ai)
如果事件 A 1 , A 2 . . . . . . A n A_1,A_2......A_n A1,A2......An构成一个完备事件组,都有正概率且彼此互斥。则对任意事件B,有如下公式(即全概率公式):
![]()
也就是: P ( B ) = ∑ i = 1 n P ( A i ) P ( B ∣ A i ) P(B)=\sum_{i=1}^nP(A_i)P(B|A_i) P(B)=∑i=1nP(Ai)P(B∣Ai)
其实就是把所有情况罗列出来:“ A 1 A_1 A1发生时B发生”、“ A 2 A_2 A2发生时B发生”、…、“ A n A_n An发生时B发生”,B的发生总会在其中之一,都加起来就得到了B发生的概率。
全概率公式_肖潇不吃洋芋的博客-CSDN博客_全概率公式
4.似然函数
似然性:“似然性”(likelihood)和“概率”(probability)意思相近,都是指某种事件发生的可能性。在统计学中,似然性”和“概率”又有明确的区分,概率用于在已知一些参数的情况下,预测接下来的观测所得到的结果,而似然性则是用于在已知某些观测所得到的结果时,对有关事物的性质的参数进行估计。
经常会有文章提到先验概率,后验概率及似然概率,他们的意思可以这么理解:
1)先验——根据若干年的统计(经验)或者气候(常识),某地方下雨的概率;
2)似然——下雨(果)的时候有乌云(因/证据/观察的数据)的概率,即已经有了果,对证据发生的可能性描述;
3)后验——根据天上有乌云(原因或者证据/观察数据),下雨(结果)的概率;
一般认为,在上述公式中,P(A),P(B)是先验概率,P(B|A)是似然概率,P(A|B) 是后验概率。
似然函数:
定义:给定输出x时,关于参数θ的似然函数L(θ|x)(在数值上)等于给定参数θ后变量X的概率:
![]()
其中,小x是指联合样本随机变量X取到的值。θ是指未知参数,属于参数空间。
p(x|θ)可以看作有两个变量的函数。
当θ设为常量,则你会得到一个关于x的概率函数(probability function),对于不同的样本点x,其出现概率是多少;
当x设为常量,你将得到关于θ的似然函数(likelihood function),对于不同的参数θ,出现x这个样本点的概率是多少。
例:
- 抛一枚匀质硬币,抛10次,6次正面向上的可能性多大? 这是概率。
- 抛一枚硬币,抛10次,结果是6次正面向上,且是匀质的可能性多大?这是似然,求参数。
注:匀质的可能性代表正面向上和反面向上是等可能的,均为0.5。
最大似然函数:
极大似然估计是指已知某个随机样本满足某种概率分布,利用结果反推出导致结果的参数值。
例:抛一枚硬币,抛10次,结果是6次正面朝上,最有可能导致这种结果的参数是多少?
注:某个参数为多少时,抛10次中,结果是6次正面朝上的概率最大。
最大似然法的步骤:
- 写出似然函数。
- 如果无法直接求导的话,对似然函数取对数。
- 求导数,令导数为0,得到似然方程。
- 解方程,得到参数结果。
为何使用对数似然函数?
求解一个函数的极大化往往需要求解该函数的关于未知参数的偏导数,但直接求导会使计算变得更为复杂。所以借助对数似然函数。因为对数函数是单调增函数,所以极大值点会相同。
注:概率值是小数,多个连乘的情况下,会导致结果接近于0,此时对似然函数取对数的负数,变成最小化对数似然函数。
最大似然法、似然函数及对数似然函数_YaoHa_的博客-CSDN博客
4.概率生成模型
理论与定义:
假设 x x x有两种类别 C 1 C_1 C1和 C 2 C_2 C2,而我们要分辨 x x x属于那种类别,我们可以计算 x x x分别属于两种类别的概率。这样就把分类问题转化为了概率计算问题。
1.通过贝叶斯公式我们可以知道 x x x属于类别 C 1 C_1 C1的概率为
P ( C 1 ∣ x ) = P ( x ∣ C 1 ) P ( C 1 ) P ( x ) = P ( x ∣ C 1 ) P ( C 1 ) P ( x ∣ C 1 ) P ( C 1 ) + P ( x ∣ C 2 ) P ( C 2 ) P(C_1|x)=\frac{P(x|C_1)P(C_1)}{P(x)}=\frac{P(x|C_1)P(C_1)}{P(x|C_1)P(C_1)+P(x|C_2)P(C_2)} P(C1∣x)=P(x)P(x∣C1)P(C1)=P(x∣C1)P(C1)+P(x∣C2)P(C2)P(x∣C1)P(C1),此时如果 P ( C 1 ∣ x ) > 0.5 P(C_1|x)>0.5 P(C1∣x)>0.5,则我们认为类别为 C 1 C_1 C1,否则类别为 C 2 C_2 C2。
2.所谓概率生成模型意思就是可以通过这个模型生成一个 x x x。
具体来说就是,我们可以通过 P ( x ) = P ( x ∣ C 1 ) P ( C 1 ) + P ( x ∣ C 2 ) P ( C 2 ) P(x)=P(x|C_1)P(C_1)+P(x|C_2)P(C_2) P(x)=P(x∣C1)P(C1)+P(x∣C2)P(C2)计算出 P ( x ) P(x) P(x),就可以知道 x x x的分布,进而生成 x x x。
如果想要计算出 P ( x ) P(x) P(x),就要根据训练集估计出 P ( C 1 ) P(C_1) P(C1)、 P ( x ∣ C 1 ) P(x|C_1) P(x∣C1)、 P ( C 2 ) P(C_2) P(C2)、 P ( x ∣ C 2 ) P(x|C_2) P(x∣C2)这四个值。
更直观一点地讲,每个类别就是一个多元正态分布,其中多元是因为每个样本有多个维度的特征。
3.可以根据数据集中属于两个类别的对象的数量计算 P ( C 1 ) P(C_1) P(C1)和 P ( C 2 ) P(C_2) P(C2)这两个先验概率(Prior Probability)。
如果有2个样本属于类别 C 1 C_1 C1,4个样本属于类别 C 2 C_2 C2,那 P ( C 1 ) = 1 3 P(C_1)=\frac{1}{3} P(C1)=31、 P ( C 2 ) = 2 3 P(C_2)=\frac{2}{3} P(C2)=32。
4.要计算后验概率(Posterior Probability) P ( x ∣ C 1 ) P(x|C_1) P(x∣C1)和 P ( x ∣ C 2 ) P(x|C_2) P(x∣C2),可以假设训练集中的各类别样本的特征分别是从某个多元正态分布(多元对应特征的多维)中取样得到的,或者说是假设训练集中各类别样本的特征分别符合某多元正态分布。
该正态分布的输入是一个样本的特征 x x x,输出为样本 x x x是从这个正态分布取样得到(或者说该样本属于某类别)的概率密度,然后通过积分就可以求得 P ( x ∣ C 1 ) P(x|C_1) P(x∣C1)和 P ( x ∣ C 2 ) P(x|C_2) P(x∣C2)。
5.正态分布公式为 f μ , Σ ( x ) = 1 ( 2 π ) D 2 1 ∣ Σ ∣ 1 2 e − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) f_{\mu,\Sigma}(x)=\frac{1}{(2\pi)^{\frac{D}{2}}}\frac{1}{|\Sigma|^{\frac{1}{2}}}e^{-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)} fμ,Σ(x)=(2π)2D1∣Σ∣211e−21(x−μ)TΣ−1(x−μ)。
正态分布有2个参数,即均值 μ \mu μ(代表正态分布的中心位置)和协方差矩阵(Covariance Matrix) Σ \Sigma Σ(代表正态分布的离散程度),计算出均值 μ \mu μ和协方差 Σ \Sigma Σ即可得到该正态分布。
公式中的 D D D为多维特征的维度。
6.实际上从任何一个正态分布中取样都有可能得到训练集中的特征,只是概率不同而已。通过极大似然估计(Maximum Likelihood Estimate,MLE),我们可以找到取样得到训练集特征的概率最大的那个正态分布,假设其均值和协方差矩阵为 μ ∗ \mu^* μ∗和 Σ ∗ \Sigma^* Σ∗。
-
根据某正态分布的均值 μ \mu μ和协方差 Σ \Sigma Σ,可以计算出从该正态分布取样得到训练集的概率。 L ( μ , Σ ) = f μ , Σ ( x 1 ) f μ , Σ ( x 2 ) … f μ , Σ ( x N ) L(\mu,\Sigma)=f_{\mu,\Sigma}(x^1)f_{\mu,\Sigma}(x^2)\dots f_{\mu,\Sigma}(x^N) L(μ,Σ)=fμ,Σ(x1)fμ,Σ(x2)…fμ,Σ(xN),这就是似然函数(Likelihood Function),其中 N N N是训练集中某个类别样本的数量。
-
μ ∗ , Σ ∗ = a r g m a x μ , Σ L ( μ , Σ ) \mu^*,\Sigma^*=arg\ max_{\mu,\Sigma}L(\mu,\Sigma) μ∗,Σ∗=arg maxμ,ΣL(μ,Σ)。
当然可以求导。
直觉: μ ∗ = 1 N ∑ i = 1 N x i \mu^*=\frac{1}{N}\sum_{i=1}^Nx^i μ∗=N1∑i=1Nxi, Σ ∗ = 1 N ∑ i = 1 N ( x i − μ ∗ ) ( x i − μ ∗ ) T \Sigma^*=\frac{1}{N}\sum_{i=1}^N(x^i-\mu^*)(x^i-\mu^*)T Σ∗=N1∑i=1N(xi−μ∗)(xi−μ∗)T。
协方差矩阵共享
每个类别的特征符合一个多元正态分布,每个多元正态分布也有不同的均值和协方差矩阵。让每个类别对应的多元正态分布共享一个协方差矩阵(各个协方差矩阵的加权平均和),公式为 Σ = N 1 N 1 + N 2 Σ 1 + N 2 N 1 + N 2 Σ 2 \Sigma=\frac{N_1}{N_1+N_2}\Sigma^1+\frac{N_2}{N_1+N_2}\Sigma^2 Σ=N1+N2N1Σ1+N1+N2N2Σ2,可以减少模型参数,缓解过拟合。
极大似然估计
-
定义
极大似然估计指已知某个随机样本满足某种概率分布,但是其中具体的参数不清楚,然后通过若干次试验,观察其结果,利用结果推出参数的大概值。一般说来,在一次试验中如果事件A发生了,则认为此时的参数值会使得 P ( A ∣ θ ) P(A|\theta) P(A∣θ)最大,极大似然估计法就是要这样估计出的参数值,使所选取的样本在被选的总体中出现的可能性为最大。
-
求极大似然函数估计值的一般步骤:
- 写出似然函数
- 对似然函数取对数,并整理。取对数的原因是对数比较简单计算,并且对数是单调递增函数,所以极大值点是不变的
- 求导数
- 解似然方程
-
当共享协方差矩阵时
此时似然函数是 L ( μ 1 , μ 2 , Σ ) = f μ 1 , Σ ( x 1 ) f μ 2 , Σ ( x 2 ) … f μ 1 , Σ ( x N 1 ) × f μ 2 , Σ ( x N 1 + 1 ) f μ 2 , Σ ( x N 1 + 2 ) … f μ 2 , Σ ( x N 1 + N 2 ) L(\mu^1,\mu^2,\Sigma)=f_{\mu^1,\Sigma}(x^1)f_{\mu^2,\Sigma}(x^2)\dots f_{\mu^1,\Sigma}(x^{N_1})\times f_{\mu^2,\Sigma}(x^{N_1+1})f_{\mu^2,\Sigma}(x^{N_1+2})\dots f_{\mu^2,\Sigma}(x^{N_1+N_2}) L(μ1,μ2,Σ)=fμ1,Σ(x1)fμ2,Σ(x2)…fμ1,Σ(xN1)×fμ2,Σ(xN1+1)fμ2,Σ(xN1+2)…fμ2,Σ(xN1+N2),其中 N 1 N_1 N1为训练集中类别 C 1 C_1 C1的样本数、 N 2 N_2 N2为训练集中类别 C 2 C_2 C2的样本数。
当只有两个类别、两个特征时,如果共享协方差矩阵,那最终得到的两个类别的分界线是直线(横纵轴是两个特征),这一点可以在下文解释。

-
除了正态分布,还可以用其它的概率模型。
比如对于二值特征,可以使用伯努利分布(Bernouli Distribution)。
-
朴素贝叶斯分类
如果假设样本各个维度的数据是互相独立的,那这就是朴素贝叶斯分类器(Naive Bayes Classfier)。
4.Sigmoid函数
由上面我们知道 P ( C 1 ∣ x ) = P ( x ∣ C 1 ) P ( C 1 ) P ( x ∣ C 1 ) P ( C 1 ) + P ( x ∣ C 2 ) P ( C 2 ) = 1 1 + P ( x ∣ C 2 ) P ( C 2 ) P ( x ∣ C 1 ) P ( C 1 ) P(C_1|x)=\frac{P(x|C_1)P(C_1)}{P(x|C_1)P(C_1)+P(x|C_2)P(C_2)}=\frac{1}{1+\frac{P(x|C_2)P(C_2)}{P(x|C_1)P(C_1)}} P(C1∣x)=P(x∣C1)P(C1)+P(x∣C2)P(C2)P(x∣C1)P(C1)=1+P(x∣C1)P(C1)P(x∣C2)P(C2)1,
令 z = l n P ( x ∣ C 1 ) P ( C 1 ) P ( x ∣ C 2 ) P ( C 2 ) z=ln\frac{P(x|C_1)P(C_1)}{P(x|C_2)P(C_2)} z=lnP(x∣C2)P(C2)P(x∣C1)P(C1),则 P ( C 1 ∣ x ) = P ( x ∣ C 1 ) P ( C 1 ) P ( x ∣ C 1 ) P ( C 1 ) + P ( x ∣ C 2 ) P ( C 2 ) = 1 1 + P ( x ∣ C 2 ) P ( C 2 ) P ( x ∣ C 1 ) P ( C 1 ) = 1 1 + e − z = σ ( z ) P(C_1|x)=\frac{P(x|C_1)P(C_1)}{P(x|C_1)P(C_1)+P(x|C_2)P(C_2)}=\frac{1}{1+\frac{P(x|C_2)P(C_2)}{P(x|C_1)P(C_1)}}=\frac{1}{1+e^{-z}}=\sigma(z) P(C1∣x)=P(x∣C1)P(C1)+P(x∣C2)P(C2)P(x∣C1)P(C1)=1+P(x∣C1)P(C1)P(x∣C2)P(C2)1=1+e−z1=σ(z),这就是Sigmoid函数。
如果共享协方差矩阵,经过运算可以得到 z = w T ⋅ x + b z=w^T\cdot x+b z=wT⋅x+b的形式,其中常量 w T = ( μ 1 − μ 2 ) T Σ − 1 w^T=(\mu^1-\mu^2)^T\Sigma^{-1} wT=(μ1−μ2)TΣ−1,
常量 b = − 1 2 ( μ 1 ) T ( Σ 1 ) − 1 μ 1 + 1 2 ( μ 2 ) T ( Σ 2 ) − 1 μ 2 + l n N 1 N 2 b=-\frac{1}{2}(\mu^1)^T(\Sigma^1)^{-1}\mu^1+\frac{1}{2}(\mu^2)^T(\Sigma^2)^{-1}\mu^2+ln\frac{N_1}{N_2} b=−21(μ1)T(Σ1)−1μ1+21(μ2)T(Σ2)−1μ2+lnN2N1,即形如 P ( C 1 ∣ x ) = σ ( w ⋅ x + b ) P(C_1|x)=\sigma(w\cdot x+b) P(C1∣x)=σ(w⋅x+b)。
我们最终得到了一个这么简单的一个式子,有一个问题是,我们假设了分布、用了一堆概率,为什么不能直接定义线性模型呢?该问题的答案在下一篇笔记。
4分类模型之逻辑回归
逻辑回归
假设训练集如下,有2个类别 C 1 C_1 C1和 C 2 C_2 C2,表格中的每列为一个样本。
例如,第一列表示样本 x 1 x^1 x1的类别为 C 1 C_1 C1,所以它的标签 y ^ 1 \hat y^1 y^1是1。
| x 1 x^1 x1 | x 2 x^2 x2 | x 3 x^3 x3 | … \dots … | x N x^N xN |
|---|---|---|---|---|
| C 1 C_1 C1 | C 1 C_1 C1 | C 2 C_2 C2 | … \dots … | C 1 C_1 C1 |
| y ^ 1 = 1 \hat y^1=1 y^1=1 | y ^ 2 = 1 \hat y^2=1 y^2=1 | y ^ 3 = 0 \hat y^3=0 y^3=0 | … \dots … | y ^ N = 1 \hat y^N=1 y^N=1 |
模型定义
在分类(Classification)一节中,我们 要找到一个模型 P w , b ( C 1 ∣ x ) P_{w,b}(C_1|x) Pw,b(C1∣x),如果 P w , b ( C 1 ∣ x ) ≥ 0.5 P_{w,b}(C_1|x)\geq0.5 Pw,b(C1∣x)≥0.5,则 x x x属于类别 C 1 C_1 C1,否则属于类别 C 2 C_2 C2。
可知 P w , b ( C 1 ∣ x ) = σ ( z ) P_{w,b}(C_1|x)=\sigma(z) Pw,b(C1∣x)=σ(z),其中 σ ( z ) = 1 1 + e − z \sigma(z)=\frac{1}{1+e^{-z}} σ(z)=1+e−z1(Sigmoid Function), z = w ⋅ x + b = ∑ i = 1 N w i x i + b z=w\cdot x+b=\sum_{i=1}^Nw_ix_i+b z=w⋅x+b=∑i=1Nwixi+b。
最终我们找到了模型 f w , b ( x ) = σ ( ∑ i = 1 N w i x i + b ) f_{w,b}(x)=\sigma(\sum_{i=1}^Nw_ix_i+b) fw,b(x)=σ(∑i=1Nwixi+b),这其实就是逻辑回归(Logistic Regression)。(逻辑回归是分类,不是回归)
评价模型好坏
损失函数:
从模型 f w , b ( x ) = P w , b ( C 1 ∣ x ) f_{w,b}(x)=P_{w,b}(C_1|x) fw,b(x)=Pw,b(C1∣x)中取样得到训练集的概率为: L ( w , b ) = f w , b ( x 1 ) f w , b ( x 2 ) ( 1 − f w , b ( x 3 ) ) … f w , b ( x N ) L(w,b)=f_{w,b}(x^1)f_{w,b}(x^2)(1-f_{w,b}(x^3))\dots f_{w,b}(x^N) L(w,b)=fw,b(x1)fw,b(x2)(1−fw,b(x3))…fw,b(xN)(似然函数)。
上述模型是咱们训练出来的模型,我们需要一个指标去评价他的好坏,用这种方法去评价:先选出一个分类里的类别,比如C1。而后根据训练集里数据的实际标签去一个个测试模型,比如X1的实际标签是C1,我们就用模型测试一下X1是C1的概率;X3的实际标签是C2,我们就用模型测试一下X3不是C1的概率(二分类)。把每一个数据的相关概率相乘(似然函数),便是该模型能够完整无误的得到训练集所有正确标签的概率。显然这个概率越接近1,这个模型就越好。
我们要求 w ∗ , b ∗ = a r g m a x w , b L ( w , b ) w^*,b^*=arg\ max_{w,b}L(w,b) w∗,b∗=arg maxw,bL(w,b)我们希望找到能使损失函数最大的w和b,等同于 w ∗ , b ∗ = a r g m i n w , b ( − l n L ( w , b ) ) w^*,b^*=arg\ min_{w,b}(-lnL(w,b)) w∗,b∗=arg minw,b(−lnL(w,b))取对数计算更简单,且单调性不变,加上负号等同于找最小(对数似然方程,Log-likelihood Equation)。
而 − l n L ( w , b ) = − l n f w , b ( x 1 ) − l n f w , b ( x 2 ) − l n ( 1 − f w , b ( x 3 ) ) … -lnL(w,b)=-lnf_{w,b}(x^1)-lnf_{w,b}(x^2)-ln(1-f_{w,b}(x^3))\dots −lnL(w,b)=−lnfw,b(x1)−lnfw,b(x2)−ln(1−fw,b(x3))…,其中 l n f w , b ( x n ) = y ^ n l n f w , b ( x n ) + ( 1 − y ^ n ) l n ( 1 − f ( x n ) ) lnf_{w,b}(x^n)=\hat y^nlnf_{w,b}(x^n)+(1-\hat y^n)ln(1-f(x^n)) lnfw,b(xn)=y^nlnfw,b(xn)+(1−y^n)ln(1−f(xn))其中\hat y^n:1 for class 1,0 for class 2,所以 − l n L ( w , b ) = ∑ n = 1 N − [ y ^ n l n f w , b ( x n ) + ( 1 − y ^ n ) l n ( 1 − f w , b ( x n ) ) ] -lnL(w,b)=\sum_{n=1}^N-[\hat y^nlnf_{w,b}(x^n)+(1-\hat y^n)ln(1-f_{w,b}(x^n))] −lnL(w,b)=∑n=1N−[y^nlnfw,b(xn)+(1−y^n)ln(1−fw,b(xn))],式中 n n n用来选择某个样本。
假设有两个伯努利分布 p p p和 q q q,在 p p p中有 p ( x = 1 ) = y ^ n , p ( x = 0 ) = 1 − y ^ n p(x=1)=\hat y^n,p(x=0)=1-\hat y^n p(x=1)=y^n,p(x=0)=1−y^n,在 q q q中有 q ( x = 1 ) = f ( x n ) , q ( x = 0 ) = 1 − f ( x n ) q(x=1)=f(x^n),q(x=0)=1-f(x^n) q(x=1)=f(xn),q(x=0)=1−f(xn),则 p p p和 q q q的交叉熵(Cross Entropy,代表两个分布有多接近,两个分布一模一样时交叉熵为0)为 H ( p , q ) = − ∑ x p ( x ) l n ( q ( x ) ) H(p,q)=-\sum_xp(x)ln(q(x)) H(p,q)=−∑xp(x)ln(q(x))。
所以损失函数 L ( f ) = ∑ n = 1 N C ( f ( x n ) , y ^ n ) L(f)=\sum_{n=1}^NC(f(x^n),\hat y^n) L(f)=∑n=1NC(f(xn),y^n),其中 C ( f ( x n ) , y ^ n ) = − [ y ^ n l n f w , b ( x n ) + ( 1 − y ^ n ) l n ( 1 − f w , b ( x n ) ) ] C(f(x^n),\hat y^n)=-[\hat y^nlnf_{w,b}(x^n)+(1-\hat y^n)ln(1-f_{w,b}(x^n))] C(f(xn),y^n)=−[y^nlnfw,b(xn)+(1−y^n)ln(1−fw,b(xn))],即损失函数为所有样本的 f ( x n ) f(x^n) f(xn)与 y ^ n \hat y^n y^n的交叉熵之和,式中 n n n用来选择某个样本。
梯度
− l n L ( w , b ) ∂ w i = ∑ n = 1 N − ( y ^ n − f w , b ( x n ) ) x i n \frac{-lnL(w,b)}{\partial w_i}=\sum_{n=1}^{N}-(\hat y^n-f_{w,b}(x^n))x_i^n ∂wi−lnL(w,b)=∑n=1N−(y^n−fw,b(xn))xin(推导过程省略,具体见李宏毅机器学习视频14分56秒),其中 i i i用来选择数据的某个维度, n n n用来选择某个样本, N N N为数据集中样本个数。
该式表明,预测值与label相差越大时,参数更新的步幅越大,这符合常理。
4.逻辑回归与线性回归比较

注释:step 2逻辑回归里评价模型的好坏是用Cross entropy: C ( f ( x n ) , y ^ n ) = − [ y ^ n l n f w , b ( x n ) + ( 1 − y ^ n ) l n ( 1 − f w , b ( x n ) ) ] C(f(x^n),\hat y^n)=-[\hat y^nlnf_{w,b}(x^n)+(1-\hat y^n)ln(1-f_{w,b}(x^n))] C(f(xn),y^n)=−[y^nlnfw,b(xn)+(1−y^n)ln(1−fw,b(xn))],即损失函数为所有样本的 f ( x n ) f(x^n) f(xn)与 y ^ n \hat y^n y^n的交叉熵之和,式中 n n n用来选择某个样本。
线性回归里的loss function是: L ( f ) = L ( w , b ) = ∑ n = 1 10 ( y ^ − ( b + w ⋅ x n ) ) 2 L(f)=L(w,b)=\sum_{n=1}^{10}(\hat y-(b+w\cdot x^n))^2 L(f)=L(w,b)=∑n=110(y^−(b+w⋅xn))2,也就是所有样本误差的平方和。
模型
逻辑回归模型比线性回归模型多了一个sigmoid函数;
逻辑回归输出是[0,1],而线性回归的输出是任意值。
损失函数
逻辑回归模型使用的训练集中label的值必须是0或1,而线性回归模型训练集中label的值是真实值。
图中线性回归损失函数中的 1 2 \frac{1}{2} 21是为了方便求导
这里有一个问题,为什么逻辑回归模型中不使用Square Error呢?这个问题的答案见下文
梯度
逻辑回归模型和线性回归模型的梯度公式一样
4.为什么逻辑回归模型中不使用Square Error

由上图可知,当label的值为1时,不管预测值是0还是1,梯度都为0,当label值为0时也是这样。
如下图所示,如果在逻辑回归中使用Square Error,当梯度接近0时,我们无法判断目前与最优解的距离,也就无法调节学习率;并且在大多数时候梯度都是接近0的,收敛速度会很慢。
距离目标很远的时候,cross entropy的微分值很大,可以快速的接近目标。
但是square error在距离目标很远的时候微分值依然很小,这样接近目标的过程会很缓慢
而且,在很接近目标的时候应该把学习率调低,但是square error你不知道你距离目标还有多远
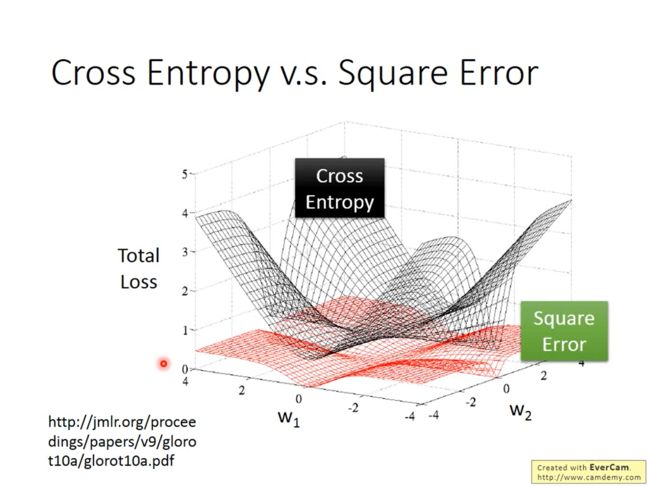
4.判别模型VS生成模型
形式对比
逻辑回归是一个判别模型(Discriminative Model),用正态分布描述后验概率(Posterior Probability)则是生成模型(Generative Model)。
如果生成模型中共用协方差矩阵,那两个模型/函数集其实是一样的,都是 P ( C 1 ∣ x ) = σ ( w ⋅ x + b ) P(C_1|x)=\sigma(w\cdot x+b) P(C1∣x)=σ(w⋅x+b)。
因为做了不同的假设,即使是使用同一个数据集、同一个模型,找到的函数是不一样的。
优劣对比
-
如果现在数据很少,当假设了概率分布之后,就可以需要更少的数据用于训练,受数据影响较小;而判别模型就只根据数据来学习,易受数据影响,需要更多数据。
-
当假设了概率分布之后,生成模型受数据影响较小,对噪声的鲁棒性更强。
-
对于生成模型来讲,先验的和基于类别的概率(Priors and class-dependent probabilities),即 P ( C 1 ) P(C_1) P(C1)和 P ( C 2 ) P(C_2) P(C2),可以从不同的来源估计得到。以语音识别为例,如果使用生成模型,可能并不需要声音的数据,网上的文本也可以用来估计某段文本出现的概率。
语音辨识是generative模型,peiors的probabilities是某句话被说出来的概率,预估这个概率并不需要有声音的data,只需要去网络上爬取很多的文字就可以计算出某段文字出现的机率,而class-dependent probabilities的部分才需要声音和文字。这样子的priors很精确
4.多分类
(Multi-class Classification)
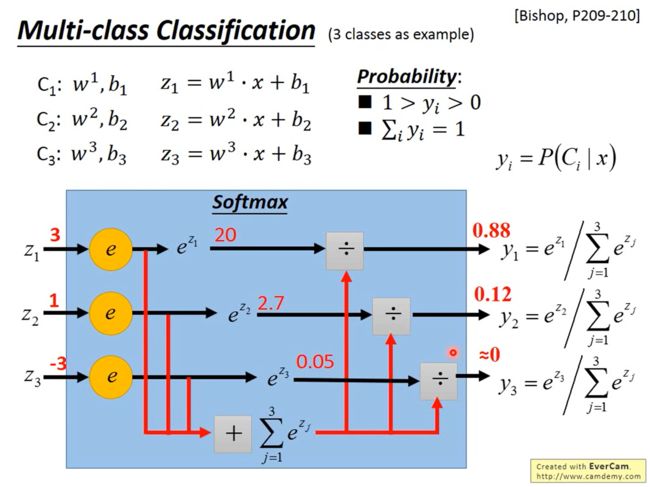
以3个类别 C 1 C_1 C1、 C 2 C_2 C2和 C 3 C_3 C3为例,分别对应参数 w 1 , b 1 w^1,b_1 w1,b1、 w 2 , b 2 w^2,b_2 w2,b2和 w 3 , b 3 w^3,b_3 w3,b3,即 z 1 = w 1 ⋅ x + b 1 z_1=w^1\cdot x+b_1 z1=w1⋅x+b1、 z 2 = w 2 ⋅ x + b 2 z_2=w^2\cdot x+b_2 z2=w2⋅x+b2和 z 3 = w 3 ⋅ x + b 3 z_3=w^3\cdot x+b_3 z3=w3⋅x+b3。

Z1、Z2、Z3可以是任何值,丢进softmax后output的值是正的,且是0到1,且总和等于1。
Softmax
softmax会使大的值更大,小的值更小
使用Softmax( y i = e z i ∑ j = 1 3 e z j y_i=\frac{e^{z_i}}{\sum_{j=1}^3e^{z_j}} yi=∑j=13ezjezi),使得 0 < y i < 1 0
Softmax公式中为什么要用 e e e?这是有原因/可解释的,可以看下PRML,也可以搜下最大熵。
最大熵(Maximum Entropy)其实也是一种分类器,和逻辑回归一样,只是从信息论的角度来看待。
损失函数
计算预测值 y y y和 y ^ \hat y y^的交叉熵, y y y和 y ^ \hat y y^都是一个向量,即 − ∑ i = 1 3 y ^ i l n y i -\sum_{i=1}^3\hat y^ilny^i −∑i=13y^ilnyi。
这时需要使用one-hot编码:如果 x ∈ C 1 x\in C_1 x∈C1,则 y = [ 1 0 0 ] y=\begin{bmatrix}1\\0\\0\end{bmatrix} y=⎣⎡100⎦⎤;如果 x ∈ C 2 x\in C_2 x∈C2,则 y = [ 0 1 0 ] y=\begin{bmatrix}0\\1\\0\end{bmatrix} y=⎣⎡010⎦⎤;如果 x ∈ C 3 x\in C_3 x∈C3,则 y = [ 0 0 1 ] y=\begin{bmatrix}0\\0\\1\end{bmatrix} y=⎣⎡001⎦⎤。
梯度
和逻辑回归的思路一样。
4.逻辑回归的局限
如下图所示,假如有2个类别,数据集中有4个样本,每个样本有2维特征,将这4个样本画在图上。
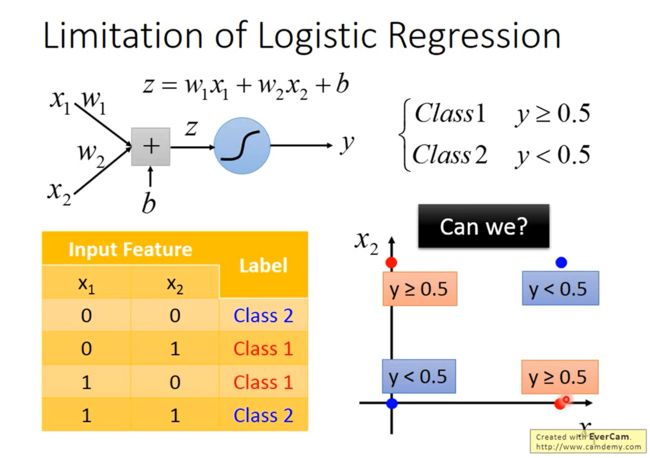
如下图所示,假如用逻辑回归做分类,即 y = σ ( z ) = σ ( w 1 x 1 + w 2 x 2 + b ) y=\sigma(z)=\sigma(w_1x_1+w_2x_2+b) y=σ(z)=σ(w1x1+w2x2+b),我们找不到一个可以把“蓝色”样本和“红色”样本间隔开的函数。
假如一定要用逻辑回归,那我们可以怎么办呢?我们可以尝试特征变换(Feature Transformation)。
事实上单个逻辑回归单元的作用是有限的
4.特征变换
(Feature Transformation)
在上面的例子中,我们并不能找到一个能将蓝色样本和红色样本间隔开的函数。
如下图所示,我们可以把原始的数据/特征转换到另外一个空间,在这个新的特征空间中,找到一个函数将“蓝色”样本和“红色”样本间隔开。
比如把原始的两维特征变换为与 [ 0 0 ] \begin{bmatrix}0\\0\end{bmatrix} [00]和 [ 1 1 ] \begin{bmatrix}1\\1\end{bmatrix} [11]的距离,在这个新的特征空间中,“蓝色”样本和“红色”样本是可分的。
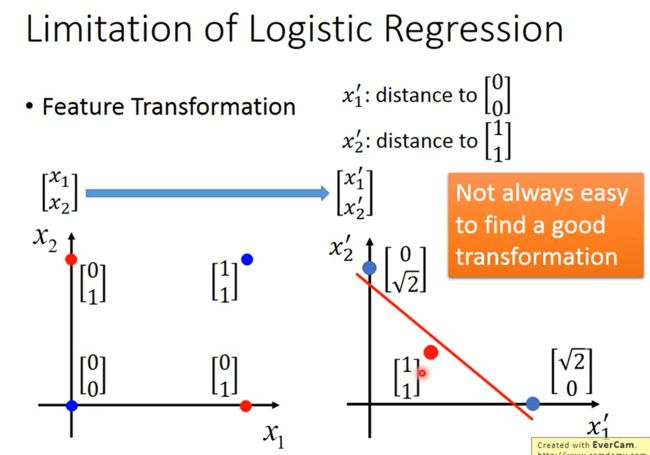
但有一个问题是,我们并不一定知道怎么进行特征变换。或者说我们想让机器自己学会特征变换,这可以通过级联逻辑回归模型实现,即把多个逻辑回归模型连接起来,如下图所示。
下图中有3个逻辑回归模型,根据颜色称它们为小蓝、小绿和小红。小蓝和小绿的作用是分别将原始的2维特征变换为新的特征 x 1 ′ x_1' x1′和 x 2 ′ x_2' x2′,小红的作用是在新的特征空间 [ x 1 ′ x 2 ′ ] \begin{bmatrix}x_1'\\x_2'\end{bmatrix} [x1′x2′]上将样本分类。
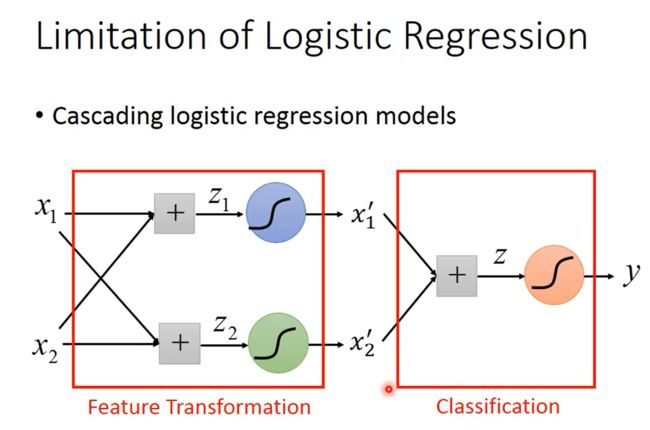
如下图所示,举一个例子。小蓝的功能是(下图左上角),离 ( 1 , 0 ) (1,0) (1,0)越远、离 ( 0 , 1 ) (0,1) (0,1)越近,则 x 1 ′ x_1' x1′越大;小蓝的功能是(下图左下角),离 ( 1 , 0 ) (1,0) (1,0)越远、离 ( 0 , 1 ) (0,1) (0,1)越近,则 x 2 ′ x_2' x2′越小。小蓝和小绿将特征映射到新的特征空间 [ x 1 ′ x 2 ′ ] \begin{bmatrix}x_1'\\x_2'\end{bmatrix} [x1′x2′]中,结果见下图右下角,然后小红就能找到一个函数将“蓝色”样本和“红色”样本间隔开。
4.神经网络(Neural Network)
假如把上例中的一个逻辑回归叫做神经元(Neuron),那我们就形成了一个神经网络。
5.深度学习
深度学习的三个步骤
和机器学习一样:
-
确定模型(Model)/函数集(Function Set),在深度学习中就是定义一个神经网络。
不同的连接会构成多样的网络结构。
-
确定如何评价函数的好坏
如果是多分类,那和Classification一章中一样,计算每个样本预测结果与Ground Truth的交叉熵,然后求和,即为Loss。
-
确定如何找到最好的函数
还是Gradient Descent。
神经网络模型对应的函数比较复杂,而反向传播算法(Backpropagation)是一个很有效的计算神经网络梯度的方法。
神经网络的结构
-
输入层(Input Layer)
实际上就是输入,并不是真正的“层”。
-
隐藏层(Hidden Layers)
输入层和输出层之间的层。Deep指有很多隐藏层,多少层才算Deep并没有统一标准。
可以看成特征提取器(Feature Extractor),作用是代替特征工程(Feature Engineering)。
-
输出层(Output Layer)
最后一层。
可以看成分类器
全连接前馈神经网络
即Fully Connected Feedforward Neural Network,FFN。
- 全连接是指每个神经元与上一层的所有神经元相连。
- 前馈神经网络(FNN,Feedforward Neural Network)是指各神经元分层排列,每个神经元只与前一层的神经元相连,接收前一层的输出,并输出给下一层,各层间没有反馈。
一些网络
其中Residual Net并不是一般的全连接前馈神经网络
| 网络结构 | 提出年份 | 层数 | ImageNet错误率 |
|---|---|---|---|
| AlexNet | 2012 | 8 | 16.4% |
| VGGNet | 2014 | 19 | 7.3% |
| GoogleNet | 2014 | 22 | 6.7% |
| Residual Net | 2015 | 152 | 3.57% |
机器学习和深度学习的工作重点
- 在机器学习中,人类需要手工做特征工程(Feature Engineering),人类需要思考如何提取特征。
- 有了深度学习以后,人类可以不做特征工程,但也遇到了新的问题:人类需要设计合适的网络结构。
这两个问题哪个更容易呢?可能后者更容易些,比如在图像识别、语音识别任务中,人类可能并不知道自己是如何识别图像和语音的,就无法通过符号主义进行特征工程。
关于深度学习的一些疑问
-
虽然深度学习的的准确度很高,但是它使用的参数更多,参数多、准确度高也是很正常的事,所以有什么特别之处呢?
-
只用一个神经元足够多的隐藏层,这个模型就包括了任意函数,那为什么不这么做而非要深度呢?为什么要是Deep而不是Fat呢?
-
如何设计神经网络的结构?
多少层?每一层有多少个神经元?
只能凭经验(实验结果)和直觉,当然可以让机器自己去找网络结构,即网络架构搜索(NAS,Network Architecture Search)。
-
必须用全连接前馈神经网络吗?
不是。比如卷积神经网络(Convolutional Neural Networks, CNN)。
下面一步步给出答案
5.神经网络为什么要是深度的
为什么是“深度”神经网络?
问题与答案
-
矮胖的神经网络和高瘦的神经网络,假设它们参数量相同,哪一个更好呢?
2011年有一个实验,证明在参数量相当的情况下,高瘦的神经网络(即深度神经网络)的准确度更高,因为深度可以实现模块化。
-
只用一个神经元足够多的隐藏层,这个模型就包括了任意函数,那为什么不这么做呢?
这样确实可以包括任意函数,但实现的效率不高。
相关网址http://neuralnetworksanddeeplearning.com/chap4.html,也可以通过谷歌等找找其它答案。
“深度”的好处
-
模块化(Modularization)
-
就像写程序一样,我们不能把所有代码写在main函数里,而需要通过定义函数等方式将程序模块化。
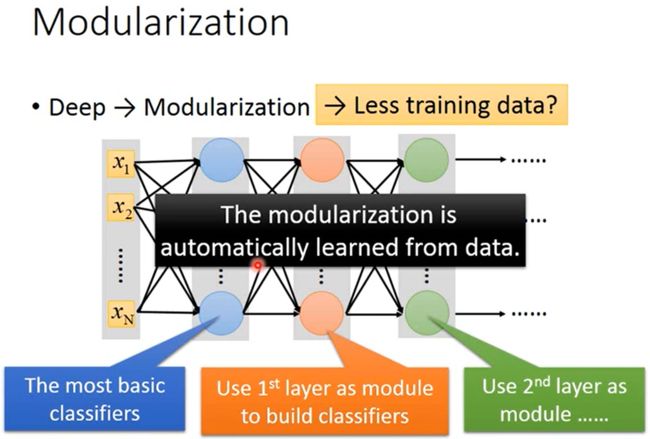
如下图所示,假如要做一个图片的四分类,两个维度分别是头发长短和性别,如果使用矮胖的神经网络会遇到一个问题,就是短头发的女生样本和长头发的男生样本会比较少,那这两个类别的分类器就会比较差。

如下图所示,我们可以先定义各属性的分类器(Classifiers for the attributes),即先定义性别和头发长短的分类器,然后再做四分类。这样第一层分类器就不会遇到样本少的问题,第二层的分类器也容易训练,整体上也需要更少的训练集。
-
在深度神经网络中,每层网络都可以作为下一层网络使用的一个模块,并且这个模块化是通过机器学习自动得到的。
常有“人工智能=机器学习+大数据”的说法,但实际上“深度”使得需要的数据更少,如果数据集无限大,根本就不需要机器学习,只要去数据库里拿就好了。深度学习也并不是通过大量参数暴力拟合出一个模型,反而是在通过模块化有效利用数据。
这里只是一个图像分类的例子,“深度”产生的模块化在语音识别任务中也有体现,与逻辑电路也有相似的问题和结论,具体可以看李宏毅视频。
-
-
端到端学习(End-to-end Learning)
深度神经网络模型就像是把一个个函数串接在一起,每个函数负责某个功能,每个函数负责什么功能是通过机器学习根据数据自动确定的。李宏毅视频中有讲这一点在语音识别、CV任务中的体现。
-
处理复杂任务
有时类似的输入要输出差别很大的结果,比如白色的狗和北极熊看起来差不多,但分类结果非常不同;有时差别很大的输入要输出相同的结果,比如火车正面和侧面的图片都应该被分类成火车。
只有一个隐藏层的网络是无法处理这种任务的。李宏毅视频中有讲这一点在语音识别、CV任务中的体现。
-
其它
Do deep nets really need to be deep?
李宏毅视频里也还有很多关于“深度”的探讨。
5.神经网络中的反向传播算法
链式法则(Chain Rule)
- z = h ( y ) , y = g ( x ) → d z d x = d z d y d y d x z=h(y),y=g(x)\to\frac{dz}{dx}=\frac{dz}{dy}\frac{dy}{dx} z=h(y),y=g(x)→dxdz=dydzdxdy
- z = k ( x , y ) , x = g ( s ) , y = h ( s ) → d z d s = d z d x d x d s + d z d y d y d s z=k(x,y),x=g(s),y=h(s)\to\frac{dz}{ds}=\frac{dz}{dx}\frac{dx}{ds}+\frac{dz}{dy}\frac{dy}{ds} z=k(x,y),x=g(s),y=h(s)→dsdz=dxdzdsdx+dydzdsdy
反向传播算法(Backpropagation)
变量定义
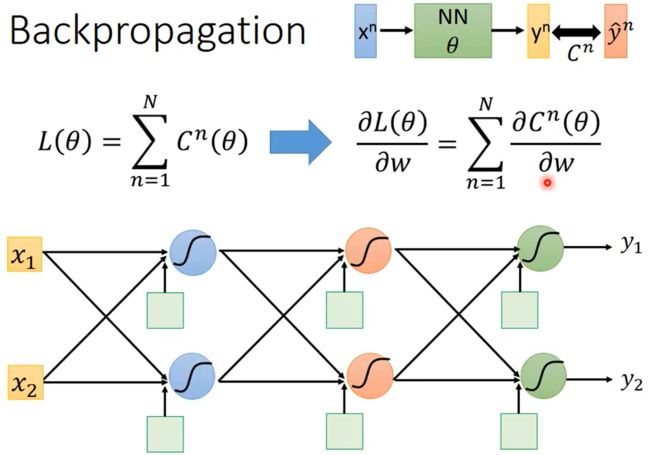
如下图所示,设神经网络的输入为 x n x^n xn,该输入对应的label是 y ^ n \hat y^n y^n,神经网络的参数是 θ \theta θ,神经网络的输出是 y n y^n yn。
整个神经网络的Loss为 L ( θ ) = ∑ n = 1 N C n ( θ ) L(\theta)=\sum_{n=1}^{N}C^n(\theta) L(θ)=∑n=1NCn(θ)。假设 θ \theta θ中有一个参数 w w w,那 ∂ L ( θ ) ∂ w = ∑ n = 1 N ∂ C n ( θ ) ∂ w \frac{\partial L(\theta)}{\partial w}=\sum^N_{n=1}\frac{\partial C^n(\theta)}{\partial w} ∂w∂L(θ)=∑n=1N∂w∂Cn(θ)。
一个神经元的情况
如下图所示, z = x 1 w 1 + x 2 w x + b z=x_1w_1+x_2w_x+b z=x1w1+x2wx+b,根据链式法则可知 ∂ C ∂ w = ∂ z ∂ w ∂ C ∂ z \frac{\partial C}{\partial w}=\frac{\partial z}{\partial w}\frac{\partial C}{\partial z} ∂w∂C=∂w∂z∂z∂C,其中为所有参数 w w w计算 ∂ z ∂ w \frac{\partial z}{\partial w} ∂w∂z是Forward Pass、为所有激活函数的输入 z z z计算 ∂ C ∂ z \frac{\partial C}{\partial z} ∂z∂C是Backward Pass。
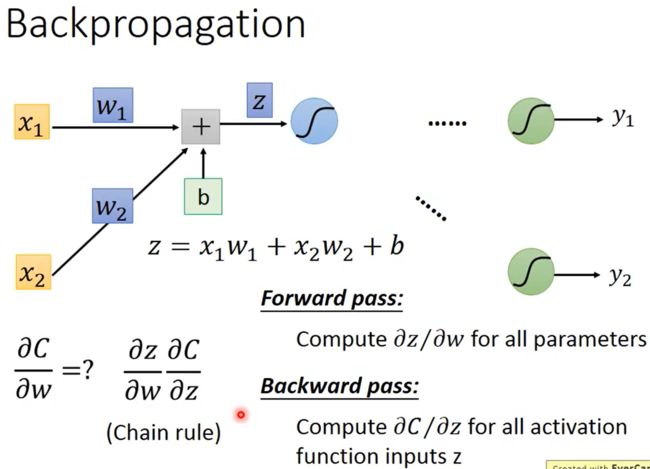
Forward Pass
Forward Pass是为所有参数 w w w计算 ∂ z ∂ w \frac{\partial z}{\partial w} ∂w∂z,它的方向是从前往后算的,所以叫Forward Pass。
以一个神经元为例,因为 z = x 1 w 1 + x 2 w x + b z=x_1w_1+x_2w_x+b z=x1w1+x2wx+b,所以 ∂ z ∂ w 1 = x 1 , ∂ z ∂ w 2 = x 2 \frac{\partial z}{\partial w_1}=x_1,\frac{\partial z}{\partial w_2}=x_2 ∂w1∂z=x1,∂w2∂z=x2,如下图所示。

规律是:该权重乘以的那个输入的值。所以当有多个神经元时,如下图所示。

Backward Pass
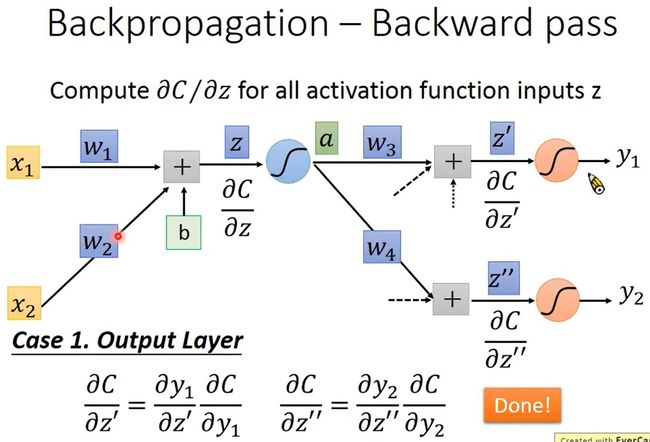
Backward Pass是为所有激活函数的输入 z z z计算 ∂ C ∂ z \frac{\partial C}{\partial z} ∂z∂C,它的方向是从后往前算的,要先算出输出层的 ∂ C ∂ z \frac{\partial C}{\partial z} ∂z∂C,再往前计算其它神经元的 ∂ C ∂ z \frac{\partial C}{\partial z} ∂z∂C,所以叫Backward Pass。
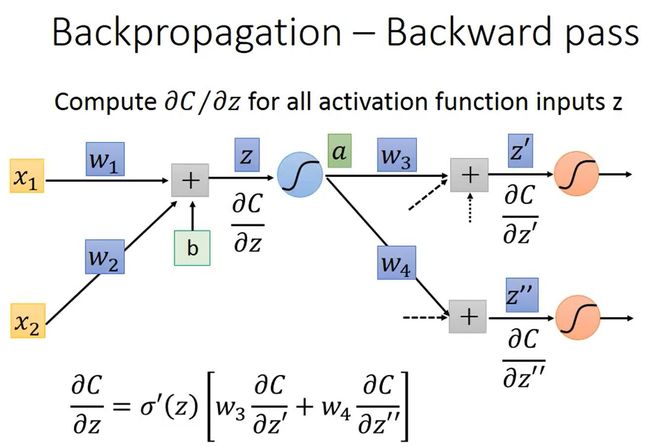
如上图所示,令 a = σ ( z ) a=\sigma(z) a=σ(z)就是z经过sigmoid之后得到a,根据链式法则,可知 ∂ C ∂ z = ∂ a ∂ z ∂ C ∂ a \frac{\partial C}{\partial z}=\frac{\partial a}{\partial z}\frac{\partial C}{\partial a} ∂z∂C=∂z∂a∂a∂C,其中 ∂ a ∂ z = σ ′ ( z ) \frac{\partial a}{\partial z}=\sigma'(z) ∂z∂a=σ′(z)
==就是sigmoid方程的微分(如下图)==是一个常数。因为在Forward Pass时 z z z的值就已经确定了,而 ∂ C ∂ a = ∂ z ′ ∂ a ∂ C ∂ z ′ + ∂ z ′ ′ ∂ a ∂ C ∂ z ′ ′ = w 3 ∂ C ∂ z ′ + w 4 ∂ C ∂ z ′ ′ \frac{\partial C}{\partial a}=\frac{\partial z'}{\partial a}\frac{\partial C}{\partial z'}+\frac{\partial z''}{\partial a}\frac{\partial C}{\partial z''}=w_3\frac{\partial C}{\partial z'}+w_4\frac{\partial C}{\partial z''} ∂a∂C=∂a∂z′∂z′∂C+∂a∂z′′∂z′′∂C=w3∂z′∂C+w4∂z′′∂C,所以 ∂ C ∂ z = σ ′ ( z ) [ w 3 ∂ C ∂ z ′ + w 4 ∂ C ∂ z ′ ′ ] \frac{\partial C}{\partial z}=\sigma'(z)[w_3\frac{\partial C}{\partial z'}+w_4\frac{\partial C}{\partial z''}] ∂z∂C=σ′(z)[w3∂z′∂C+w4∂z′′∂C]。
对于式子 ∂ C ∂ z = σ ′ ( z ) [ w 3 ∂ C ∂ z ′ + w 4 ∂ C ∂ z ′ ′ ] \frac{\partial C}{\partial z}=\sigma'(z)[w_3\frac{\partial C}{\partial z'}+w_4\frac{\partial C}{\partial z''}] ∂z∂C=σ′(z)[w3∂z′∂C+w4∂z′′∂C],我们可以发现两点:
-
∂ C ∂ z \frac{\partial C}{\partial z} ∂z∂C的计算式是递归的,因为在计算 ∂ C ∂ z \frac{\partial C}{\partial z} ∂z∂C的时候需要计算 ∂ C ∂ z ′ \frac{\partial C}{\partial z'} ∂z′∂C和 ∂ C ∂ z ′ ′ \frac{\partial C}{\partial z''} ∂z′′∂C。
如下图所示,输出层的 ∂ C ∂ z ′ \frac{\partial C}{\partial z'} ∂z′∂C和 ∂ C ∂ z ′ ′ \frac{\partial C}{\partial z''} ∂z′′∂C是容易计算的。
-
∂ C ∂ z \frac{\partial C}{\partial z} ∂z∂C的计算式 ∂ C ∂ z = σ ′ ( z ) [ w 3 ∂ C ∂ z ′ + w 4 ∂ C ∂ z ′ ′ ] \frac{\partial C}{\partial z}=\sigma'(z)[w_3\frac{\partial C}{\partial z'}+w_4\frac{\partial C}{\partial z''}] ∂z∂C=σ′(z)[w3∂z′∂C+w4∂z′′∂C]是一个神经元的形式
如下图所示,只不过没有嵌套sigmoid函数而是乘以一个常数 σ ′ ( z ) \sigma'(z) σ′(z),每个 ∂ C ∂ z \frac{\partial C}{\partial z} ∂z∂C都是一个神经元的形式,所以可以通过神经网络计算 ∂ C ∂ z \frac{\partial C}{\partial z} ∂z∂C。

总结
- 通过Forward Pass,为所有参数 w w w计算 ∂ z ∂ w \frac{\partial z}{\partial w} ∂w∂z;
- 通过Backward Pass,为所有激活函数的输入 z z z计算 ∂ C ∂ z \frac{\partial C}{\partial z} ∂z∂C;
- 最后 ∂ C ∂ w = ∂ C ∂ z ∂ z ∂ w \frac{\partial C}{\partial w}=\frac{\partial C}{\partial z}\frac{\partial z}{\partial w} ∂w∂C=∂z∂C∂w∂z,也就求出了梯度。
6.神经网络训练问题与解决方案
明确问题类型及其对应方法
在深度学习中,一般有两种问题:
- 在训练集上性能不好
- 在测试集上性能不好。
当一个方法被提出时,它往往是针对这两个问题其中之一的,比如dropout方法是用来处理在测试集上性能不好的情况。
处理神经网络在训练集上性能不好的情况的方法
-
修改神经网络架构,比如换成更好的激活函数
sigmoid函数会导致梯度消失,可以换成ReLU、Leaky ReLU、Parametric ReLU、Maxout
-
调整学习率
比如RMSProp、Momentum、Adam
处理神经网络在测试集上性能不好的情况的方法
-
Early Stopping、Regularization,这两个是比较传统的方法,不只适用于深度学习
-
Dropout,比较有深度学习的特色
一些性能优化方法的简介
下面3点都是在增加模型的随机性,鼓励模型做更多的exploration。
-
Shuffling
输入数据的顺序不要固定,mini-batch每次要重新生成
-
Dropout
鼓励每个神经元都学到东西,也可以广义地理解为增加随机性
-
Gradient noise
2015年提出,计算完梯度后,加上Gaussian noise。
随着迭代次数增加,noise应该逐渐变小。
下面3点是关于学习率调整的技巧
-
warm up
开始时学习率较小,等稳定之后学习率变大
-
Curriculum learning
2009年提出,先使用简单的数据训练模型(一方面此时模型比较弱,另一方面在clean data中更容易提取到核心特征),然后再用难的数据训练模型。
这样可以提高模型的鲁棒性。
-
Fine-tuning
下面3点是关于数据预处理的技巧,避免模型学习到太极端的参数
-
Normalization
有Batch Normalization、Instance Normalization、Group Normalization、Layer Normalization、Positional Normalization
-
Regularization
6.神经网络精度低不一定是因为过拟合
-
相比于决策树等方法,神经网络更不容易过拟合。
K近邻、决策树等方法在训练集上更容易得到100%等很高的正确率,神经网络一般不能,训练神经网络首先遇到的问题一般是在训练集上的精度不高。
-
不要总是把精度低归咎于过拟合
如果模型在训练集上精度高,对于K近邻、决策树等方法我们可以直接判断为过拟合,但对于神经网络来说我们还需要检查神经网络在测试集上的精度。如果神经网络在训练集上精度高但在测试集上精度低,这才说明神经网络过拟合了。
如果56层的神经网络和20层的神经网络相比,56层网络在测试集上的精度低于20层网络,这还不能判断为56层网络包含了过多参数导致过拟合。一般来讲,56层网络优于20层网络,但如果我们发现56层网络在训练集上的精度本来就低于20层网络,那原因可能有很多而非过拟合,比如56层网络没训练好导致一个不好的局部最优、虽然56层网络的参数多但结构有问题等等。
感兴趣可以看看ResNet论文Deep Residual Learning for Image Recognition,这篇论文可能与该问题有关。
6.梯度消失
定义:1980年代常用的激活函数是sigmoid函数。在使用sigmoid函数时会发现随着神经网络层数的增加,识别准确率逐渐下降,这个现象的原因并不是过拟合(原因见上文),而是梯度消失。

如上图所示,当神经网络层数很多时,靠近输入层的参数梯度很小,靠近输出层的参数梯度很大;当学习率一样时,就会导致靠近输入层的参数更新很慢,靠近输出层的参数更新较快。进而,当输出层的参数已经更新到接近收敛时,输入层的参数几乎还是随机的状态。
原因:我们尝试解释一下上述的原因是什么。为什么靠近输入层的参数梯度小、靠近输出层的参数梯度大呢?梯度事实上就是相关的变化率。根据反向传播算法公式: ∂ C ∂ z = ∂ a ∂ z ∂ C ∂ a \frac{\partial C}{\partial z}=\frac{\partial a}{\partial z}\frac{\partial C}{\partial a} ∂z∂C=∂z∂a∂a∂C,其中 ∂ a ∂ z = σ ′ ( z ) \frac{\partial a}{\partial z}=\sigma'(z) ∂z∂a=σ′(z),是sigmoid方程的微分,是一个常数,且范围是0~0.25。可以看到这是一个小于1的数,当计算梯度时每经过一层就有一个sigmoid方程就要乘以一个该微分,就越小。由于反向传播算法是从输出层开始的,因此越接近输入层梯度就越小。
我们也可以用一种直观的方式去解释。直观上,sigmoid方程的输入范围是无穷的,输出范围是[0,1]。因此sigmoid方程里输入变化导致的输出变化是比较小的。所谓的梯度是指某一层的参数对最终输出的变化率,sigmoid方程一层层的叠起来,当距离最终输出越远时要经过的sigmoid方程是越多的,该层输入变化幅度对最终输出变化幅度的影响显然是被削弱的很严重的。简单地说,在距离最终输出“超级远”的地方输入有一个很大的变化,经过很多层的sigmoid方程削弱后最终输出几乎感受不到你的这个变化。
这种靠近输入层梯度很小的情况会导致靠近输入层的参数更新的非常缓慢,可能靠近输出层的参数已经更新到几乎收敛不变时(最佳位置附近),靠近输入层的参数还距离最佳位置相去甚远,几乎处于随机的状态。
如以上所说,这样的模型(靠近输入层的参数可能还处于随机的状态)性能不好是可以预见的。而根据以上分析在使用sigmoid方程的模型里,显然当神经网络层数越多时,这种情况就越明显。我们很容易以为这是过拟合,现在我们知道这其实是梯度消失导致的。
解决方法:
Hinton提出无监督逐层训练方法以解决这个问题,其基本思想是每次训练一层隐节点。
后来Hinton等人提出修改激活函数,比如换成ReLU。
6.ReLU等其他常用的激活函数
ReLU(Rectified Linear Unit)
定义:当输入小于等于0时,输出为0;当输入大于0时,输出等于输入。如图:
优点:
相比于sigmoid函数,它有以下优点:
- 运算更快
- 更符合生物学
- 等同于无穷多个bias不同的sigmoid函数叠加起来
- 最重要的,可以解决梯度消失问题。
怎样解决sigmoid方程里梯度消失的问题的呢?
当输入小于0时,等同于没有该“神经元”。当输入大于0时,输出等于输入,微分为1。就解决了sigmoid方程里削弱输入变化对输出变化的影响问题。
此时有个问题,RuLU函数会导致整个神经网络变成线性的吗?
先给出结论,**不会。**我们会觉得RuLU将导致神经网络变成线性的原因是RuLU这个激活函数有效的部分都是线性的。但事实上,当输入改变很小,不改变激活函数的Operation Region(操作区域)时确实是线性的。但是当输入改变很大,改变了激活函数的Operation Region时,整个神经网络就是非线性的。(os:事实上,我并未完全理解这一点,但是需要记住这个事实,即使用RuLU函数的神经网络依然是非线性的。)
Leaky ReLU
当输入小于等于0时,输出为输入的0.01倍;当输入大于0时,输出等于输入。
这样做的原因是当输入小于0的时候我们依然可以求微分,便于更新参数。如图:
Parametric ReLU
当输入小于等于0时,输出为输入的 α \alpha α倍;当输入大于0时,输出等于输入。
其中 α \alpha α是通过梯度下降学习到的参数。如图:
Maxout
定义
通过学习得到一个激活函数,人为调整将每层输出的多个值分组,然后输出每组值中的最大值。(跟maxpooling一模一样)
具体是怎么实现的呢?下面详细介绍:
把输入连接上不同的函数,人为的将不同函数的输出分组,只保留输出最大的函数,将这一层的输出作为下一层的输入继续之前的操作。
事实上RuLU是Maxout的一个特例。如下图:
根据权重不同,就会有不同的激活函数。如下图:
一组中分多少个函数会决定你的激活函数分成几段。如下图:
那要怎么去训练这样一个模型呢?
事实上我们只需要去关心输出最大值的那个函数,当成一个“瘦长”的神经网络去train就行了。如下图:
那么又出现一个问题,如下图这些输出较小值函数的权值是不是就会没被train到?
事实上不会,每一笔输入的data所得到最大值的那个函数是不同的,我们的data很多,所以权值都有很大可能被train到。
6.学习率调整方法
RMSProp
先交代一下,RMSProp其实就是给我们提供了一种思想,就是当我们在更新参数的时候不仅考虑当前梯度,还考虑以前的梯度。
-
背景
RMSProp是Adagrad的升级版,是2013年Hinton在一次录制课上提出的。
在训练神经网络时,损失函数不一定是凸函数(局部最小值即为全局最小值),可能是各种各样的函数,有时需要较大的学习率,有时需要较小的学习率,而Adagrad并不能实现这种效果,因此产生了RMSProp。
-
定义
w t + 1 = w t − η σ t g t σ 0 = g 0 , σ t = α ( σ t − 1 ) 2 + ( 1 − α ) ( g t ) 2 w^{t+1}=w^t-\frac{\eta}{\sigma^t}g^t\\ \sigma^0=g^0,\sigma^t=\sqrt{\alpha(\sigma^{t-1})^2+(1-\alpha)(g^t)^2} wt+1=wt−σtηgtσ0=g0,σt=α(σt−1)2+(1−α)(gt)2
其中 w w w是某点参数; η \eta η是学习率; g g g是梯度; α \alpha α是一个手动调整的值,根据公式,显然它代表旧的梯度的重要性,值越小则代表旧的梯度越不重要,新的梯度越重要。反之亦然。如下图所示就是RMSProp的作用过程: -
神经网络中很难找到最优的参数吗?
面临的问题有plateau、saddle point和local minima。
英文 中文 梯度 plateau 停滞期 ∂ L ∂ w ≈ 0 \frac{\partial L}{\partial w}\approx0 ∂w∂L≈0 saddle point 鞍点 ∂ L ∂ w = 0 \frac{\partial L}{\partial w}=0 ∂w∂L=0 local minima 局部最小值 ∂ L ∂ w = 0 \frac{\partial L}{\partial w}=0 ∂w∂L=0 2007年有人指出神经网络的error surface是很平滑的,没有很多局部最优。
假设有1000个参数,一个参数处于局部最优的概率是 p p p,则整个神经网络处于局部最优的概率是 p 1000 p^{1000} p1000,这个概率是很小的。
Momentum
1986年提出
-
如何处理停滞期、鞍点、局部最小值等问题?
考虑现实世界中物体具有惯性、动量(Momentum)的特点,尽可能避免“小球”陷入error surface上的这几种位置。
-
定义
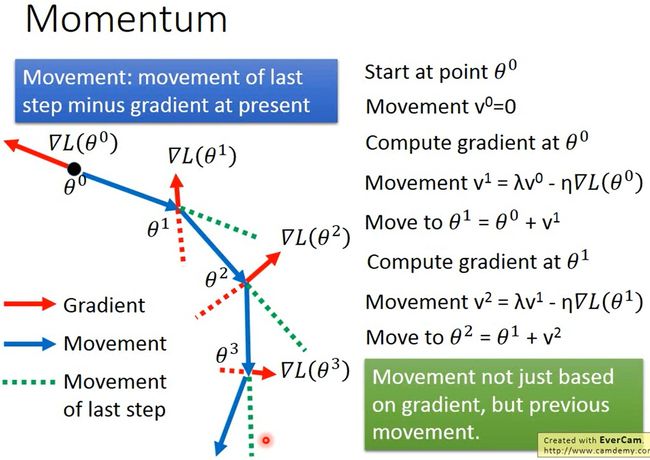
如下图所示,不仅考虑当前的梯度,还考虑上一次的移动方向: v t = λ v t − 1 − η g t , v 0 = 0 v^t=\lambda v^{t-1}-\eta g^t,v^0=0 vt=λvt−1−ηgt,v0=0,
其中上标 t t t是迭代次数; v v v指移动方向(movement),类似于物理中的速度; g g g是梯度(gradient); λ \lambda λ用来控制惯性的重要性,值越大代表惯性越重要; η \eta η是学习率。
对于某一步更新参数的时候,之前所有的梯度都会都会产生影响,只是越早的梯度影响会越小。
Adam
Adam = RMSProp + Momentum + Bias Correction ,2015年提出
Adam VS SGDM
目前常用的就是Adam和SGDM。
Adam训练速度快,large generalization gap(在训练集和验证集上的性能差异大),但不稳定;SGDM更稳定,little generalization gap,更加converge(收敛)。
| 领域 | 技术/模型 | 优化器 |
|---|---|---|
| Q&A、文意理解、文章生成 | BERT | Adam |
| BERT的Backbone、翻译 | Transformer | Adam |
| 语音生成 | Tacotron | Adam |
| 目标检测 | YOLO | SGDM |
| 目标检测 | Mask R-CNN | SGDM |
| 图片分类 | ResNet | SGDM |
| 图片生成 | Big-GAN | Adam |
| 元学习 | MAML | Adam |
SGDM适用于计算机视觉,Adam适用于NLP、Speech Synthesis、GAN、Reinforcement Learning。
SWATS
2017年提出,尝试把Adam和SGDM结合,其实就是前一段时间用Adam,后一段时间用SGDM,但在切换时需要解决一些问题。
尝试改进Adam
-
AMSGrad
-
Adam的问题
Non-informative gradients contribute more than informative gradients.
在Adam中,之前所有的梯度都会对第 t t t步的movement产生影响。然而较早阶段(比如第1、2步)的梯度信息是相对无效的,较晚阶段(比如 t − 1 t-1 t−1、 t − 2 t-2 t−2步)的梯度信息是相对有效的。在Adam中,可能发生较早阶段梯度相对于较晚阶段梯度比重更大的问题。
-
提出AMSGrad
2018年提出
-
-
AdaBound
2019年提出,目的也是改进Adam。
-
Adam需要warm up吗?需要
warm up:开始时学习率小,后面学习率大。
因为实验结果说明在刚开始的几次(大概是10次)迭代中,参数值的分布比较散乱(distort),因此梯度值就比较散乱,导致梯度下降不稳定。
-
RAdam
2020年提出
-
Lookahead
2019年提出,像一个wrapper一样套在优化器外面,适用于Adam、SGDM等任何优化器。
迭代几次后会回头检查一下。
-
Nadam
2016年提出,把NAG的概念应用到Adam上。
-
AdamW
2017年提出,这个优化器还是有重要应用的(训练出了某个BERT模型)。
尝试改进SGDM
-
LR range test
2017年提出
-
Cyclical LR
2017年提出
-
SGDR
2017年提出,模拟Cosine但并不是Cosine
-
One-cycle LR
2017年提出,warm-up+annealing+fine-tuning
-
SGDW
2017年提出,
改进Momentum
-
背景
如果梯度指出要停下来,但动量说要继续走,这样可能导致坏的结果。
-
NAG(Nesterov accelerated gradient)
1983年提出,会预测下一步。
Early Stopping
如果学习率调整得较好,随着迭代次数增加,神经网络在训练集上的loss会越来越小,但因为验证集(Validation set)==事实上这里的验证集也是用于训练的,跟“训练集”不同的是验证集没有在模型里选练过。验证集一般就是从训练集里切片出来的一部分数据,他不参与模型训练,而只用于验证模型对未训练过的数据的性能。==和训练集不完全一样,所以神经网络在验证集上的loss可能不降反升,所以我们应该在神经网络在验证集上loss最小时停止训练。
Keras文档中就有关于Early stopping的说明。
6.如何提高神经网络的鲁棒性
正则化
正则化(Regularization)就是重新定义损失函数,新的损失函数为原损失函数与正则项(Regularization term)的求和。
在做正则化时,一般不考虑参数中的bias,因为正则化的目的是使函数更平滑,而函数中的bias与函数的平滑程度通常是无关的。
-
L2正则化
L ′ ( θ ) = L ( θ ) + λ 1 2 ∣ ∣ θ ∣ ∣ 2 L'(\theta)=L(\theta)+\lambda\frac{1}{2}\vert\vert\theta\vert\vert_2 L′(θ)=L(θ)+λ21∣∣θ∣∣2
新的损失函数就是原损失函数加上一个正则项。 L ( θ ) L(\theta) L(θ)是原损失函数, λ 1 2 ∣ ∣ θ ∣ ∣ 2 \lambda\frac{1}{2}\vert\vert\theta\vert\vert_2 λ21∣∣θ∣∣2是正则项。这里的1/2是为了下面的微分方便
其中 θ = { w 1 , w 2 , … } \theta=\{w_1,w_2,\dots\} θ={w1,w2,…}, ∣ ∣ θ ∣ ∣ 2 = ( w 1 ) 2 + ( w 2 ) 2 + … \vert\vert\theta\vert\vert_2=(w_1)^2+(w_2)^2+\dots ∣∣θ∣∣2=(w1)2+(w2)2+…想要使新的损失函数最小,就要求原损失函数项接近0,也就是力求在训练集上使模型输出与标签接近;正则项接近0就要求各个参数也要接近0。
此时新的损失函数的梯度为KaTeX parse error: Undefined control sequence: \part at position 7: \frac{\̲p̲a̲r̲t̲ ̲L'}{\part w}=\f…,
更新参数为KaTeX parse error: Undefined control sequence: \part at position 26: … w^t-\eta\frac{\̲p̲a̲r̲t̲ ̲L'}{\part w}=w^…,由于 η \eta η的值一般会设的很小且 λ \lambda λ的值也会设的很小,所以 1 − η λ 1-\eta\lambda 1−ηλ在一次次Update的过程中会逐渐接近1但小于1,每次参数更新时都会乘以它,最终使参数接近于0,但最后都不会变成0,因为还要减去KaTeX parse error: Undefined control sequence: \part at position 11: \eta\frac{\̲p̲a̲r̲t̲ ̲L}{\part w},最后达到平衡。
因为每次迭代参数都会变小,这一点称作weight decay(权重衰减)。
-
正则化在深度学习中有用,但没有像其在SVM中那么重要
如果用0初始化神经网络,训练神经网络时参数会逐渐远离0,通过early stopping就可以使参数尽量接近于0,这时和正则化的效果是一样的。
-
L1正则化
L ′ ( θ ) = L ( θ ) + λ 1 2 ∣ ∣ θ ∣ ∣ 1 L'(\theta)=L(\theta)+\lambda\frac{1}{2}\vert\vert\theta\vert\vert_1 L′(θ)=L(θ)+λ21∣∣θ∣∣1,其中 θ = { w 1 , w 2 , … } \theta=\{w_1,w_2,\dots\} θ={w1,w2,…}, ∣ ∣ θ ∣ ∣ 1 = ∣ w 1 ∣ + ∣ w 2 ∣ + … \vert\vert\theta\vert\vert_1=\vert w_1\vert+\vert w_ 2\vert+\dots ∣∣θ∣∣1=∣w1∣+∣w2∣+…。
此时新的损失函数的梯度为KaTeX parse error: Undefined control sequence: \part at position 7: \frac{\̲p̲a̲r̲t̲ ̲L'}{\part w}=\f…, s g n ( w ) sgn(w) sgn(w)是符号函数,代表绝对值虽然不能微分,但在Tensorflow、Keras的实际操作中都是可行的(小于0时微分为-1,大于0时微分为1,等于0时可能随便取个值?)
更新参数为KaTeX parse error: Undefined control sequence: \part at position 26: … w^t-\eta\frac{\̲p̲a̲r̲t̲ ̲L'}{\part w}=w^…,每次参数更新时都会减去一个值,或加上一个值 η λ s g n ( w t ) \eta\lambda sgn(w^t) ηλsgn(wt),这会导致最终既有较大的参数值又有较小的参数值,不像L2正则化(总是乘以一个小于1接近1)形成的都比较接近于0。
Dropout
用一定几率去删除输入层和隐藏层中的神经元,不删除输出层的神经元
-
在训练神经网络时
每个神经元被删除的概率是 p p p,每次更新参数前取样得到需要删除的神经元。
删除神经元后神经网络的结构就改变了,之后用这个新的神经网络进行训练。
对于每个mini-batch,重新取样得到需要删除的神经元。
这样训练出的模型可能会在测试集上取得好的效果,但是如果在训练集上的效果就不好还使用Dropout,很可能会更差 -
在测试神经网络时
不进行dropout、恢复使用所有的神经元,并且所有参数要乘以 1 − p 1-p 1−p,然后进行测试。
-
直观原因(Intuitive Reason)
如下图所示,神经网络中的神经元之间是团队合作关系,合作形式(激活函数)是 z = w 1 x 1 + w 2 x 2 z=w_1x_1+w_2x_2 z=w1x1+w2x2,团队中有人比较强(A),有人比较菜(B)。
在训练神经网络使用Dropout时,就相当于是让A的作用更大,让B的作用更小,但此时的目标和不使用Dropout时目标一样。
在实际中B并不是毫无用处所以还要使用B,这时因为A是被加强过的所以A和B的整体效果会超过原先目标,所以所有参数需要乘以 1 − p 1-p 1−p消除“加强”的影响(乘以与线性的激活函数是相对应的)。

-
正式理由
其实有很多种理由,这里讲李宏毅老师较为接受的一种:Dropout是一种终极的集成(ensemble)的方法。
-
Ensemble(集成学习)
复杂模型的误差一般是Bias较小,Variance较大,如果我们有多个这样的复杂模型并将平均起来,最终整体Bias和Variance就会很小。
所以我们可以把训练集分成多份,用它们分别训练出不同结构 的子模型,然后测试时用这多个子模型得到多个结果,再把多个结果取平均值。
随机森林就应用了Ensemble的思想。
-
Dropout
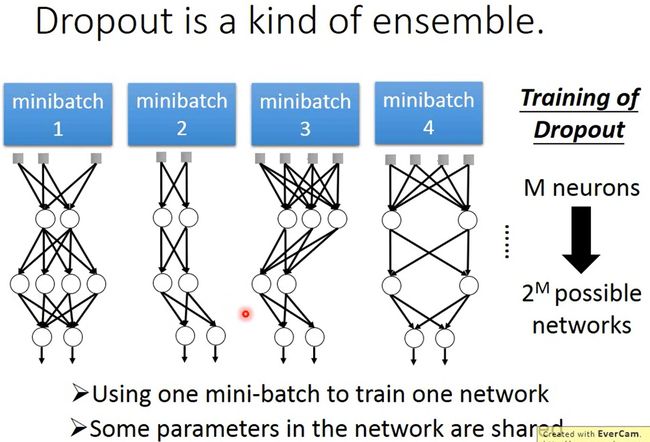
如上图所示,在Dropout中,每个mini-batch就可以训练出一个子模型,最终把这些子模型合并起来(在Dropout中就是使用全部的参数)。模型中的有些参数是共享的,也就是说一个参数可以用多个mini-batch来训练。
在测试模型时,取出每个模型然后计算结果再取平均值,这样运算量就太大了,所以通过将权重乘以 1 − p 1-p 1−p来实现平均。
为什么是乘以1-p呢?如下图所示,当激活函数是线性的时候,比如 z = w 1 x 1 + w 2 x 2 z=w_1x_1+w_2x_2 z=w1x1+w2x2,这时有2个参数 w 1 , w 2 w_1,w_2 w1,w2,通过Dropout训练模型时可能有 2 2 = 4 2^2=4 22=4个子模型,这4个子模型合并(相加)的结果 z ‘ = 2 w 1 x 1 + 2 w 2 x 2 z‘=2w_1x_1+2w_2x_2 z‘=2w1x1+2w2x2是正确结果的2倍,这时我们可以发现直接把所有参数(2个参数 w 1 , w 2 w_1,w_2 w1,w2)乘以 1 2 \frac{1}{2} 21就得到了正确结果。
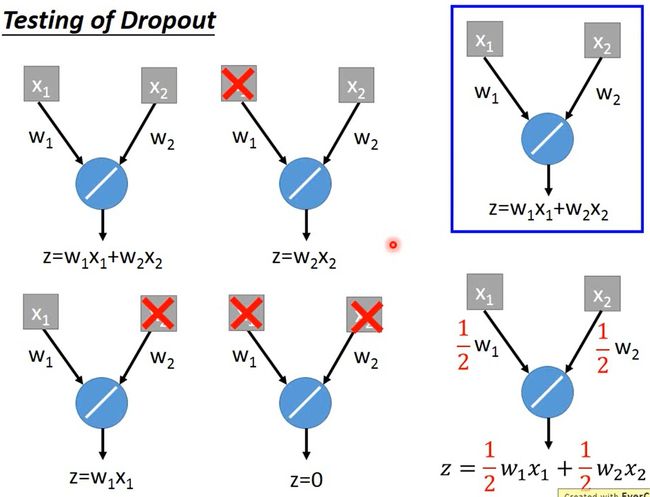
当然了,这个例子只是一个简单的线性的例子,乘以某个值这个操作是和线性函数这个前提对应的。
现实情况下神经网络不一定是线性的,所以确实不能按照完美的理论推导出Dropout是可行的,但在实验中Dropout确实有好的效果。那如果模型很接近线性模型的话,比如说用ReLU、Maxout,Dropout确实会很有效。
-
6.On-line VS Off-line
-
变量说明(Some Notations)
- x t x_t xt:第 t t t步时的输入。
- y t y_t yt:第 t t t步时模型根据 x t x_t xt和 θ t \theta_t θt计算出的结果。如果是分类,则是一个概率向量;如果是图片生成,则是一张图片。
- y ^ t \hat y_t y^t:第 t t t步时输入 x t x_t xt对应的标签/ground truth。
- θ t \theta_t θt:第 t t t步时模型的参数。
- ∇ L ( θ t ) \nabla L(\theta_t) ∇L(θt)、 g t g_t gt:模型参数为 θ t \theta_t θt时的梯度,用来计算 θ t + 1 \theta_{t+1} θt+1。
- m t + 1 m_{t+1} mt+1:从第0步到第 t t t步汇集的动量(momentum),用来计算 θ t + 1 \theta_{t+1} θt+1。
-
On-line:在第 t t t步时只能取得一对 ( x t , y ^ t ) (x_t,\hat y_t) (xt,y^t)。
-
Off-line:在第 t t t步时可以取得所有的输入 x x x及其对应的标签 y ^ \hat y y^,即在第 t t t步时计算出的 L ( θ t ) L(\theta_t) L(θt)是完整的,它只取决于 θ t \theta_t θt和整个输入 x x x,而非 x t x_t xt。
7.CNN卷积神经网络
卷积神经网络(CNN)通常被用于做图像处理。相较于其他的神经网络,CNN的优势在哪里呢?
FNN(全连接前馈神经网络)用于图像处理的缺点:
1.需要很多的参数:
假设有一张尺寸100×100的图片,输入层将会有100×100×3=30k(三原色)个像素,假设第一个隐藏层有1k个神经元,每个神经元都有这30k个参数,那么一层将会有30M个参数。这个数字已相当大。2.FNN中每一个神经元就是一个分类器,这没必要:
该架构的逻辑类似于第一个隐藏层作为最基础的pattern分类器,第二个隐藏层基于第一层做更复杂的pattern分类,以此类推。举个例子就是,第一层分类形状,第二层在形状的基础上分类材质,第三层在前两层的基础上识别具体是什么东西。
事实上,这种识别图像的方式并不符合人类的朴素认识。
识别图像时的一些特点
特点一:Some patterns are much smaller than the whole image.(有些图案比整张图片要小得多)
当在识别一张图片上的图案时,一个神经元并不需要识别一整张图片。比如当我们要去识别一张图片上的鸟,某个神经元可以把焦点放在鸟喙上,而不是每个神经元都要把一整张图片的像素都识别一遍。
特点二:The same patterns appear in different regions.(同样的图案可能出现在不同的区域)
类似于说一张图片的不同位置都出现了鸟喙,或者说有两张图片,一张图片的鸟喙出现在图片左上方,另一张图片的鸟喙出现在图片的中间,对于识别不同区域中相同的pattern的分类器我们需要分别训练他们的参数吗?不需要。我们应该让这类具有相同功能的分类器共享同一组参数。
**特点三:**Subsampling the pixels will not change the object.(对像素进行子采样不会改变对象)
CNN架构
2014年在ECCV上提出,针对上述的图片的3个性质,确定了CNN的架构如下:
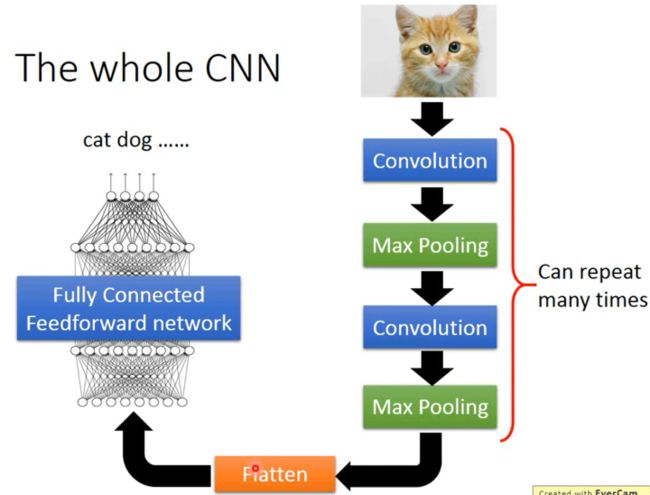
如上图所示,图片经过卷积层然后进行最大池化(max pooling),这个步骤可以进行多次;然后将数据展开(Flatten),然后将数据传进全连接前馈网络(FNN)得到最后的图片分类结果。
CNN架构作用探析
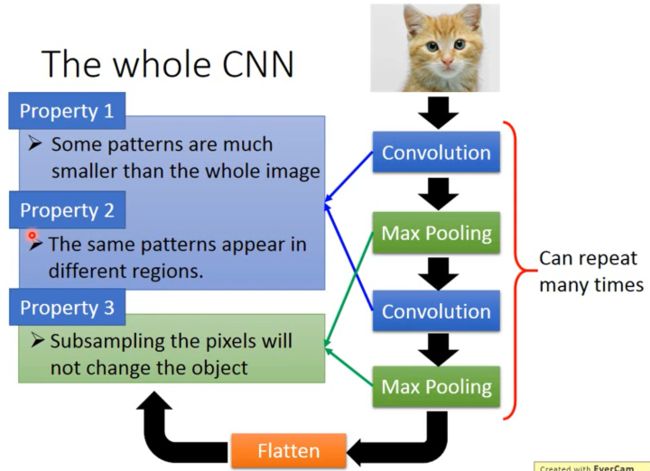
如上图所示,卷积是针对了图片的性质1和性质2,最大池化是针对了图片的性质3。
卷积(Convolution)
卷积核(kernel)和过滤器(filter)的区别_Medlen的博客-CSDN博客
深度学习笔记(3)——kernel(内核)与filter(滤波器)_江清月近人。的博客-CSDN博客
深度学习原理1——卷积计算原理(卷积核kernels、滤波器filters)_晓码bigdata的博客-CSDN博客_卷积核计算
卷积核、过滤器、通道等概念看博客去理解。
首先,卷积核(kernel)是二维的,具有长和宽,它用来对二维的输入进行扫描。
过滤器(Filter)是三维的,具有长、宽、高,它是卷积核的堆叠,堆叠的层数就是过滤器的高。
举个例子。在一个黑白图像的识别里,由于只有一层卷积核所以过滤器的“高”这个维度只有1,看起来就是二维的,此时卷积核和过滤器是相同的。
而在一个彩色图片(RGB)的识别里,有三层卷积核,所以过滤器“高”这个维度是3。
黑白图像识别为例:
如图假设我们去识别一张黑白(一个像素只有两个值)的6×6的图片。一个识别模块就是一个Filter,他是一个3×3的矩阵(Matrix),显然是一个比图片小的矩阵。事实上一个输入的每个像素只有两个值所表达的意思就是,当值是1此点为黑,当值是0此点为白。

以Filter1为例。我们用Filter1从左上角开始依次扫描整张图片(每次扫描移动的距离自己去定,本例中的stride设为1),扫描到的部分就做内积。如第一张图所示我们开始做内积,如第二张图所示扫描完整张图片,形成一个4×4的扫描结果。
事实上我们分析Filter1的作用,Filter1的主对角线元素都是1,其余都为-1,它的作用就是识别主对角线都为某种颜色的pattern,如图识别结果中左上和左下出现了最大的值,说明这两个地方出现了我们要识别的pattern。
Filter2做同样的事情,又得到一个4×4的矩阵。每一个Filter都做同样的事我们就得到很多4×4的矩阵,形成Feature Map(特征图)。
彩色图片识别为例:
如图所示,一个彩色图片(RGB)的输入有三层,称为有三个通道,逻辑是如果某层代表红®这个颜色,那么某个点是1则有红色像素,是0则没有红色像素。而此时一个Filter有三层卷积核。一个Filter(过滤器)直接与三层输入做内积,同时考虑三层通道,而不是把RGB分别考虑。
事实上卷积就是去除了某些权重的全连接网络。我们去尝试解释这件事。
我们把6×6的矩阵输入拉直成一个36个值的输入,36个值输入到一个隐藏层里,每个Filter的扫描操作相当于一个神经元(neural)只对其中的某些输入做处理,那么我们就把其他输入的权重设为0或者理解成不连接这些输入。如图所示我们只连接36个输入中的9个,并得到输出3。这样我们将使用到更少的参数。
Filter的移动扫描在神经网络里体现为另一个神经元(neural)只连接另外的9个输入,并对其做处理,并且这里的神经元参数和之前的共享。这样使用的参数在更上的基础上将再少点。
怎么去做Gradient呢?别管了,交给tool kit。
最大池化(Max Pooling)
我们把卷积得到的矩阵进行分组,如图每4个一组。最大池化是一种下采样(Subsample),下采样可以取最大值也可以取平均值。==我也不知道为何,没深究。==这里我们取最大值。
![image-20221121111045472]()
这就做完了一次Max Pooling。做完一次卷积(convolution)和最大池化(Max Pooling)在这个例子里就使得一个之前6×6的image变成了一个2×2的image。而2×2的image的每个pixel的深度是2。这个深度(channel)是多少取决于Filter有多少。
每做完一次卷积+最大池化就使得一个较大的图片变成一个较小的图片。我们可以继续把这个较小的图片再做一次卷积+最大池化。做到我们不想做为止。
这里我们可以思考一个问题,假设第一次卷积+最大池化我们有25个Filter,那么我们将得到25个特征图,再做一次有25个Filter的卷积+最大池化,是不是会得到25×25=625个特征图呢?答案是不会,依然只是会得到25个特征图。因为第一次卷积+最大池化的25个Filter得到的是一个25层通道(channel)的Image,我们在第二次的卷积+最大池化的过程中的Filter会考虑它的深度(25),就像我们在RGB辨识中做的那样。而不是每个通道单独考虑。这也就意味着一次卷积+最大池化中的Filter有多少,输出的就有多少,只是深度增加。
Flatten
这一步很简单。我们只需要把经过一些列卷积+最大值化所得到的特征图展开排列,然后作为输入丢进FNN里就行。
CNN到底学到了什么?
卷积层学到了什么?
对于第一层卷积层事实上我们很容易看出来每一个Filter在做些什么。因为其处理的输入就是原图片,filter要去处理的东西就是原图片的pixel,我们可以结合filter的参数去观察它的功能。就如同黑白图片辨识那个例子一样,对于一个3×3且主对角线参数是1的filter来说它的功能很可能就是识别主对角线为某种颜色的pattern。
但是对于第二层卷积层我们很难直观的辨识出每个filter的功能。原因在于filter要处理的输入不是pixel,而是上一次卷积+最大池化的输出,这就导致我们即使知道filter的参数,我们依然不知道它在做什么。如下图,第二层一个3×3的filter所识别的是原图片3×3的范围内的东西吗?不是。因为经过一次卷积+最大池化后的结果(也就是第二次卷积+最大池化的输入)中3×3的范围蕴含的信息不仅限于原图片3×3的范围。
那我们如何知道第二层卷积层学到了什么,或者说它在做些什么呢?如下图,第二层卷积层有50个3×3的filter,每一个filter的输出为一个11×11的矩阵(matrix),那么将有50个11×11的矩阵。对于每一个filter的11×11输出矩阵我们定义一个值叫做Degree of the activation of the k-th filter,意思是第k个filter被激活的程度,这里用激活度去称呼这个值。很容易理解的一点是filter是具有检测图片某种特征的功能,当输入的图片具有的这种功能越明显时,filter就会越被激活。衡量激活度的式子是: a k = ∑ i = 1 11 ∑ j = 1 11 a i j k a^k=\sum_{i=1}^{11}\sum_{j=1}^{11}a^k_{ij} ak=∑i=111∑j=111aijk ,代表说第k个filter输出的11×11矩阵的121个元素的累加值。累加值越大,则该filter越被激活。我们定义 x ∗ x^* x∗是使 a k a^k ak最大的那个输入图片, x ∗ = a r g m a x a k x^*=arg max a^k x∗=argmaxak。我们可以通过gradient ascent去寻找 x ∗ x^* x∗。并未深究gradient ascent是怎么实现的
如下图所示是12个filter的最大激活度输入,我们根据这些输入图片可以猜测这些filter的功能。比如说右下角的那张输入代表的filter或许是用来辨识“长长的往左下角斜的斜线”的pattern。对于flatten学到了什么,或者说想知道flatten里某个neural的功能是什么,我们可以如法炮制上面的方法。
全连接层学到了什么?
如下图,对于flatten里的某个neural我们寻找能使其输出 a j a_j aj最大的那个输入图片 x ∗ x^* x∗,根据这个 x ∗ x^* x∗pattern的特征去猜测这个neural的功能。和卷积层中不同的是全连接层里神经元学习到的是较大尺寸的pattern。
输出层学到了什么?
如下图所示,我们用同样的方法可以得到使输出层最大“激活”的 x ∗ x^* x∗。但令人疑惑的是这些对应着“0、1、2、3、4、5、6、7、8”的图片跟人类理解中的这些数字相去甚远。但这些图片在模型看来确实就是“0~8”,且激活度还相当高。事实上有相当多的例子表明机器学习到的内容和人类理解的内容是不同的。但是我们可以在寻找最大输入时通过对输入进行一些限制来找到“人类理解中的图片”。
在该数字图片识别实例中,背景色是黑色,像素是白色。
一般来说一个数字图片应该是组成数字图案的像素占整个图片的比例很小,大部分应该是非像素的背景。因此能够想到的一个限制就是整张图片像素部分应该很小或者说尽量接近于0。所以我们把最大激活度的式子做一个L1正则化的操作。
即 x ∗ = a r g M A X ( y i − ∑ i , j ∣ x i j ∣ ) x^*=argMAX(y^i-\sum_{i,j}|x_{ij}|) x∗=argMAX(yi−∑i,j∣xij∣) , x i j x_{ij} xij就是图片中的pixel,我们想让图片中的pixel最少。如下图所示,正则化之后的最大激活度图片似乎具有了一定的人类辨识度。当然还有更好的方法,更好的限制去找人类更容易理解的输入。。。
7.CNN应用案例
Deep Dream
Deep Dream的功能是让机器把它在某一层中所看到的图片 x x x的内容加到图片 x x x上。
把一张image输入进某个CNN模型,把某个隐藏层的输出(卷积+池化阶段或者全链接阶段都行)拿出来,这个输出是一个向量。我们使向量里的负值更负、正值更正。也就得到了一个特征被放大的新向量。我们把这个新向量作为目标用梯度下降的方法找到一个image,使这个image在同一个隐藏层的输出符合上面的新向量。这么做就是让CNN夸大化它看到的东西。
Deep Style
Deep Style的功能是机器抽取一张图片 x x x的内容,抽取另一张图片 y y y的风格,生成一张新的图片 z z z,使 z z z兼具 x x x的内容和 y y y的风格。类似滤镜。
A Neural Algorithm of Artistic Style这篇文章详细说了Deep Style的过程。
简单点说:
第一步:把图片 x x x丢进CNN,得到filter的output,这就是 x x x的内容(content)。
第二步:把图片 y y y丢进CNN,得到filter的output,但是我们不关注
来确实就是“0~8”,且激活度还相当高。事实上有相当多的例子表明机器学习到的内容和人类理解的内容是不同的。但是我们可以在寻找最大输入时通过对输入进行一些限制来找到“人类理解中的图片”。
在该数字图片识别实例中,背景色是黑色,像素是白色。
一般来说一个数字图片应该是组成数字图案的像素占整个图片的比例很小,大部分应该是非像素的背景。因此能够想到的一个限制就是整张图片像素部分应该很小或者说尽量接近于0。所以我们把最大激活度的式子做一个L1正则化的操作。
即 x ∗ = a r g M A X ( y i − ∑ i , j ∣ x i j ∣ ) x^*=argMAX(y^i-\sum_{i,j}|x_{ij}|) x∗=argMAX(yi−∑i,j∣xij∣) , x i j x_{ij} xij就是图片中的pixel,我们想让图片中的pixel最少。如下图所示,正则化之后的最大激活度图片似乎具有了一定的人类辨识度。当然还有更好的方法,更好的限制去找人类更容易理解的输入。。。
7.CNN应用案例
Deep Dream
Deep Dream的功能是让机器把它在某一层中所看到的图片 x x x的内容加到图片 x x x上。
把一张image输入进某个CNN模型,把某个隐藏层的输出(卷积+池化阶段或者全链接阶段都行)拿出来,这个输出是一个向量。我们使向量里的负值更负、正值更正。也就得到了一个特征被放大的新向量。我们把这个新向量作为目标用梯度下降的方法找到一个image,使这个image在同一个隐藏层的输出符合上面的新向量。这么做就是让CNN夸大化它看到的东西。
Deep Style
Deep Style的功能是机器抽取一张图片 x x x的内容,抽取另一张图片 y y y的风格,生成一张新的图片 z z z,使 z z z兼具 x x x的内容和 y y y的风格。类似滤镜。
A Neural Algorithm of Artistic Style这篇文章详细说了Deep Style的过程。
简单点说:
第一步:把图片 x x x丢进CNN,得到filter的output,这就是 x x x的内容(content)。
第二步:把图片 y y y丢进CNN,得到filter的output,但是我们不关注