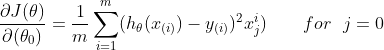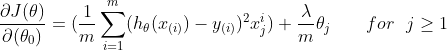吴恩达机器学习课后作业Python实现(三)：多类分类与前馈神经网络
目录
多类分类
数据集
数据可视化
正则化逻辑回归
正则化代价函数
正则化梯度
One-vs-all分类
One-vs-all预测
前馈神经网络
模型表示
模型搭建
前馈传播与预测
参考文章
多类分类
在本练习中，您将使用逻辑回归和神经网络来识别手写数字(从0到9)。自动手写数字识别在今天被广泛使用——从识别信封上的邮政编码(邮政编码)到识别银行支票上写的金额。这个练习将向您展示如何将您所学到的方法用于这个分类任务。
在练习的第一部分中，将扩展之前的逻辑回归实现，并将其应用于one-vs-all分类。
数据集
本次练习中的数据集包含了5000个手写数字存在mat格式的文件里，为Matlab的格式，因此需要使用SciPy.io的loadmat函数。
先导入练习要用的包
import numpy as np
import matplotlib.pyplot as plt
from scipy.io import loadmat # 读入matlab格式的文件
from scipy.optimize import minimize
from sklearn.metrics import classification_report # 这个包是评价报告接着加载数据，其中包含5000个训练示例，每个训练示例为20×20的数字灰度图，每个像素都有一个浮点数表示，其中20×20被转为1×400，每个训练示例为数据矩阵X的一行，每一行都是一个手写数字图像的训练示例。
训练集第二部分为5000维的向量y，它包含训练集的标签，需要注意的是由于这里是mat格式的文件，在Matlab中没有零索引，所以数字0被标记为10，而1到9按照自然顺序被标记为1到9
# 加载数据集
path = r'E:\Code\ML\ml_learning\ex3-neural network\ex3data1.mat'
data = loadmat(path)
X = data['X'] # (5000,400)
y = data['y'] # (5000,1)
数据可视化
由于数据太多，所以随机选取100张进行显示。
def plot_100_image(X):
"""
随机画100个数字
"""
# 抽100个索引
sample_idx = np.random.choice(np.arange(X.shape[0]), 100)
sample_images = X[sample_idx, :]
fig, ax_array = plt.subplots(nrows=10, ncols=10, sharey=True, sharex=True, figsize=(8, 8))
for row in range(10):
for column in range(10):
# 这里需要将数据变成20×20，且转置否则显示的图像是歪的
ax_array[row, column].matshow(sample_images[10 * row + column].reshape((20, 20)).T,
cmap='gray_r')
plt.xticks([])# 不显示刻度
plt.yticks([])
plt.show()
正则化逻辑回归
在这一部分将使用多个逻辑回归模型从而构成一个多类分类器，由于有10个数字，因此需要训练10个独立的逻辑回归分类器。在这里就不展示非正则化的逻辑回归，而直接写正则化下的公式
正则化代价函数
Sigmoid函数公式就不予展示了，正则化逻辑回归的代价函数定义如下
![J(\theta)=\frac{1}{m}\sum_{i=1}^{m}[-y^{(i)}log(h_{\theta}(x^{(i)}))-(1-y^{(i)})log(1-h_{\theta}(x^{(i)}))]+\frac{\lambda}{2m}\sum_{j=1}^{n}\theta_{j}^{2}](http://img.e-com-net.com/image/info8/3ead8a7aeeea44a18dd99e08fbaabfad.gif)
正则化梯度
需要注意θ0不需要被正则化，注意矩阵运算时的维度问题
def sigmoid(z):
return 1 / (1 + np.exp(-z))
# 正则化代价函数
def costReg(theta, X, y, learningRate):
theta = np.matrix(theta) # (1,401)
X = np.matrix(X) # (5000,401)
y = np.matrix(y) # (5000,1)
part1 = y.T * np.log(sigmoid(X * theta.T))
part2 = (1 - y.T) * np.log(1 - sigmoid(X * theta.T))
part3 = (learningRate / (2 * len(X))) * theta * theta.T
return float(-(part1 + part2) / len(X) + part3)
# 计算梯度
def gradientReg(theta, X, y, learnRate):
# 先转成矩阵才运算
theta = np.matrix(theta) # (1,401)
X = np.matrix(X) # (5000,401)
y = np.matrix(y) # (5000,1)
reg = (learnRate / len(X)) * theta
# θ0不被正则化
reg[0, 0] = 0
gradient = (X.T * (sigmoid(X * theta.T) - y)) / len(X)
return gradient + reg.T
One-vs-all分类
这一部分实现训练10个正则化逻辑回归分类器来实现手写数字识别，每个分类器对应一个分类。
def one_vs_all(X, y, num_labels, learningRate):
rows = X.shape[0] # 行5000
params = X.shape[1] # 列400
# 用于存放全部分类器的模型参数
all_theta = np.zeros((num_labels, params + 1)) # (10,401)
# 添加x0 = 1
X = np.insert(X, 0, values=np.ones(rows), axis=1)
# 通过循环训练分类器
for i in range(1, num_labels + 1):
theta = np.zeros(params + 1) # (401, )
# 1代表属于当前该类，0代表不属于该类
y_i = np.array([1 if label == i else 0 for label in y]) # (1, 400)
y_i = np.reshape(y_i, (rows, 1))# (400,1)
# 使用优化算法进行模型参数求解
fmin = minimize(fun=costReg, x0=theta, args=(X, y_i, learningRate), method='TNC', jac=gradientReg)
# 保存每一个分类器的模型参数
all_theta[i - 1, :] = fmin.x
return all_thetaOne-vs-all预测
训练完分类器后，可以使用它来预测给定图像中包含的数字。对于每个输入，应该使用经过训练的逻辑回归分类器计算它属于每个类的“概率”。您的一对所有预测函数将选择相应的逻辑回归分类器输出最高概率的类，并返回类标签(1,2，…，或K)作为输入示例的预测。
def predict_all(X, all_theta):
rows = X.shape[0] # 5000
params = X.shape[1] # 400
num_labels = all_theta.shape[0] # 10
X = np.insert(X, 0, values=np.ones(rows), axis=1)
X = np.matrix(X) # (5000,401)
all_theta = np.matrix(all_theta) # (10,401)
h = sigmoid(X * all_theta.T) # (5000, 10)
# 获得最大值的索引
h_argmax = np.argmax(h, axis=1) # (5000,1)
h_argmax = h_argmax + 1
return h_argmax 这里的h共5000行，10列，每行代表一个样本，每列是预测对应数字的概率。我们取概率最大对应的索引加1就是我们分类器最终预测出来的类别。返回的h_argmax是一个array，包含5000个样本对应的预测值。
all_theta = one_vs_all(X, y, 10, 1)
y_pred = predict_all(X, all_theta)
print(classification_report(data['y'], y_pred))然后利用classification_report对预测做评价，可以得知通过多个逻辑回归分类器得出的识别准确率为94%
precision recall f1-score support
1 0.95 0.99 0.97 500
2 0.95 0.92 0.93 500
3 0.95 0.91 0.93 500
4 0.95 0.95 0.95 500
5 0.92 0.92 0.92 500
6 0.97 0.98 0.97 500
7 0.95 0.95 0.95 500
8 0.93 0.92 0.92 500
9 0.92 0.92 0.92 500
10 0.97 0.99 0.98 500
accuracy 0.94 5000
macro avg 0.94 0.94 0.94 5000
weighted avg 0.94 0.94 0.94 5000
前馈神经网络
在前一部分实现了多类逻辑回归识别手写数字，然后，逻辑回归并不能形成更复杂的假设，在这一部分，将搭建一个前馈神经网络对相同的数据集实现识别手写数字，神经网络可以实现非常复杂的非线性模型，在这部分我们将利用已经训练好的权重进行预测
模型表示
神经网络如图上所示，它包含3层---输入层，隐含层，输出层。
模型搭建
"""加载数据集与模型参数"""
path1 = r'E:\Code\ML\ml_learning\ex3-neural network\ex3weights.mat'
weight = loadmat(path1)
theta1,theta2 = weight['Theta1'],weight["Theta2"]
# ((25, 401), (10, 26))
"""模型搭建"""
X2 = np.matrix(np.insert(data['X'], 0, values=np.ones(X.shape[0]), axis=1))
y2 = np.matrix(y)
# ((5000, 401), (5000, 1))
a1 = X2 # (5000,401)
z2 = a1 *theta1.T # (5000,25)
a2 = sigmoid(z2) # (5000,25)
a2 = np.insert(a2,0,values = np.ones(a2.shape[0]),axis = 1) # (5000,26)
z3 = a2*theta2.T # (5000, 10) theta2(10,26)
a3 = sigmoid(z3)
前馈传播与预测
"""预测"""
y_pred2 = np.argmax(a3,axis=1) + 1
print(classification_report(y2, y_pred)) precision recall f1-score support
1 0.95 0.99 0.97 500
2 0.95 0.92 0.93 500
3 0.95 0.91 0.93 500
4 0.95 0.95 0.95 500
5 0.92 0.92 0.92 500
6 0.97 0.98 0.97 500
7 0.95 0.95 0.95 500
8 0.93 0.92 0.92 500
9 0.92 0.92 0.92 500
10 0.97 0.99 0.98 500
accuracy 0.94 5000
macro avg 0.94 0.94 0.94 5000
weighted avg 0.94 0.94 0.94 5000
参考文章
https://blog.csdn.net/Cowry5/article/details/80367832