吴恩达机器学习作业Python实现(七)：K-means和PCA

目录

1 K-means聚类 

1.1 K-means实现

1.1.1 找到最近的质心

1.1.2 计算质心

1.2 在示例数据集使用K-means算法

1.3 随机初始化

1.4 图像压缩

2 PCA

2.1 示例数据集

2.2 实现PCA

2.3  PCA降维

2.3.1 将数据投影在主成分上

2.3.2 重构数据

2.3.3 可视化

2.4 人脸数据集

2.4.1 对人脸图像使用PCA

2.4.2 降维

参考文章

---

1 K-means聚类

        在本练习中，您将会使用K-means算法实现并用于图像压缩，首先从一个2D数据集开始，帮助你对K-means算法的工作原理建立直观认识，之后再运用到图像压缩上，方法是减少图像中出现的颜色的数量，只保留图像中最常见的颜色。

1.1 K-means实现

        K-means算法是一种将相似的数据自动聚类的方法，具体来说，给你一个训练集，并希望将数据分组为几个内聚的簇，其背后是一个迭代的过程，从猜测初始的质心开始，然后通过反复将样例分配到它们最近的质心来改进这个猜测，然后根据分配重新计算质心。

        算法的内循环重复执行两个步骤

• 将每个训练样本x(i)分配到最近的质心
• 使用分配给它的点重新计算每个质心的平均值

        算法总是收敛域质心的某个最终均值集，需要注意的是收敛的解决方案并非理想的，它取决于质心的初始位置，因此在实际中，往往先让算法以不同的初始质心运行几次，在不同解中选择代价函数值最小的那个。

1.1.1 找到最近的质心

        在算法的聚类分配阶段，在给定质心的当前位置下，算法将每个训练样本x(i)分配到最近的簇中心，判断最近的标准采用以下公式

 表示离样本  最近的簇中心点的索引， 是第j个簇中心点的坐标值

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.io import loadmat
from skimage import io

def findClosestCentroids(X, centroids):
    """
    用于寻找最近簇中心点
    """
    idx = []
    max_dist = 100000 # 限制最大距离
    for i in range(len(X)):
# 这里使用了numpy的广播机制，把X[i]广播成和centroids同纬度相减
        minus = X[i] - centroids  
        dist = minus[:,0]**2 + minus[:,1]**2 # 计算两点距离
        if dist.min() < max_dist: 
            ci = np.argmin(dist)
            idx.append(ci)
            
    return np.array(idx)

        接下来使用作业提供的例子，自定义了簇中心点[3, 3], [6, 2], [8, 5]，算出结果前三个点所属的簇中心应该是 [0, 2, 1]

data = loadmat(r'E:\Code\ML\ml_learning\ex7-kmeans and PCA\data\ex7data2.mat')
X = data['X']
init_centroids = np.array([[3, 3], [6, 2], [8, 5]])
idx = findClosestCentroids(X, init_centroids)
# idx[0:3] = [0, 2, 1]

1.1.2 计算质心

        根据样本在簇中心上的分配，算法的第二阶段是对每一个簇中心根据所分配到的样本，计算其平均值设定为簇中心的新坐标轴，公式如下

  是分配给簇中心k的样本集，具体来说，如果  和  属于簇中心k = 3，则

def computerCentroids(X, idx):
    centroids = []
    for i in range(len(np.unique(idx))): #去除重复数据
        u_k = X[idx==i].mean(axis=0) #计算每个簇的均值，按列求
        centroids.append(u_k)
        
    return np.array(centroids)

# computerCentroids(X, idx)
# array([[2.42830111, 3.15792418],
#        [5.81350331, 2.63365645],
#        [7.11938687, 3.6166844 ]])

1.2 在示例数据集使用K-means算法

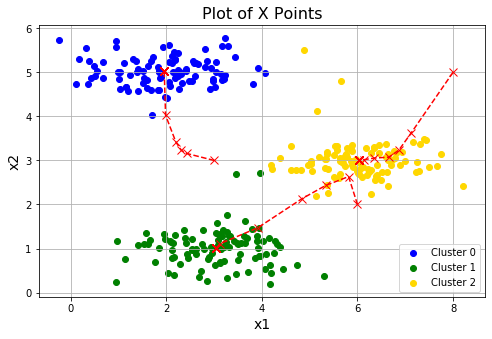
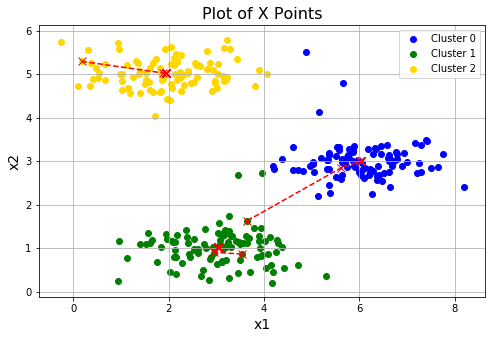
        在完成算法的两个步骤之后，我们将在一个2D数据集运行K-means算法，并将每一次迭代簇中心的坐标可视化。

def runKmeans(X, centroids, max_iters): #最大迭代次数
    K = len(centroids) # 获得簇的个数
    centroids_all = [] #用于存放簇中心点移动过程的点
    centroids_all.append(centroids) # 初始点
    centroid_i = centroids
    for i in range(max_iters):
        idx = findClosestCentroids(X, centroid_i) # 获得每次簇中心点坐标
        centroid_i = computerCentroids(X, idx) # 得到新的簇中心坐标轴
        centroids_all.append(centroid_i)
        
    return idx, centroids_all
idx, centroids_all = runKmeans(X, init_centroids, 20)
plotData(X, centroids_all, idx)

1.3 随机初始化

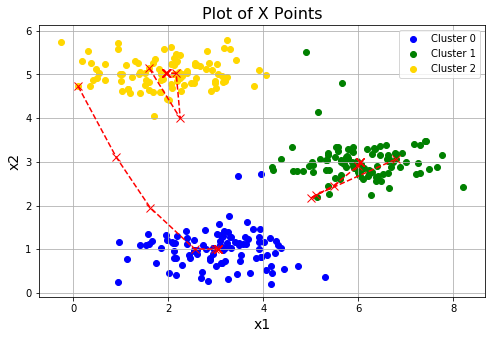
        在实践中，对簇中心点进行初始化的一个好的策略就是从训练集中选择随机的例子。

def initCentroids(X, K):
    """随机初始化"""
    m = X.shape[0]
    idx = np.random.choice(m, K) # 从m个点抽k个用于作索引
    centroids = X[idx]
    
    return centroids   

for i in range(3):
    # 随机初始化三次
    centroids = initCentroids(X,3)
    idx, centroids_all = runKmeans(X, centroids, 10)
    plotData(X, centroids_all, idx)

 

 

1.4 图像压缩

       这部分你将用K-means来进行图片压缩。在一个简单的24位颜色表示图像。每个像素被表示为三个8位无符号整数(从0到255)，指定了红、绿和蓝色的强度值。这种编码通常被称为RGB编码。我们的图像包含数千种颜色，在这一部分的练习中，你将把颜色的数量减少到16种颜色。

        这可以有效地压缩照片。具体地说，您只需要存储16个选中颜色的RGB值，而对于图中的每个像素，现在只需要将该颜色的索引存储在该位置(只需要4 bits就能表示16种可能性)。接下来我们要用K-means算法选16种颜色，用于图片压缩。你将把原始图片的每个像素看作一个数据样本，然后利用K-means算法去找分组最好的16种颜色。

def imageCompression(path, K=16):
    """图片压缩"""
    A = io.imread(path)
    A = A/255 # 将其归一到0-1
    
    X = A.reshape(-1, 3) # 把维度重塑为（128*128，3）
    centroids = initCentroids(X, K) # 获得初始簇中心点
    idx, centroids_all = runKmeans(X, centroids, 10) # 获得索引和簇中心点记录
    img = np.zeros(X.shape)  # 创建同纬度的空白照片
    centroids = centroids_all[-1] #取最后一次的簇中心点坐标
    
    for i in range(len(centroids)): #通过簇数分类像素点
        img[idx == i] = centroids[i]
    
    img = img.reshape((128, 128, 3)) #重塑为原维度
    fig, axes = plt.subplots(1, 2, figsize=(12,6))
    axes[0].imshow(A)
    axes[1].imshow(img)

path = r'E:\Code\ML\ml_learning\ex7-kmeans and PCA\data\bird_small.png'
imageCompression(path, 16)

2 PCA

        在本练习中，将使用PCA进行降维，首先先在一个2D数据集上进行，直观了解PCA如何工作，接着在5000个人脸图像数据集上降维。

2.1 示例数据集

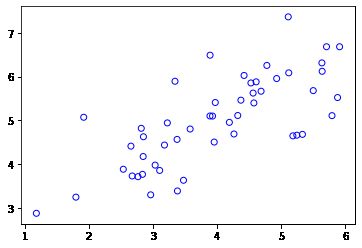
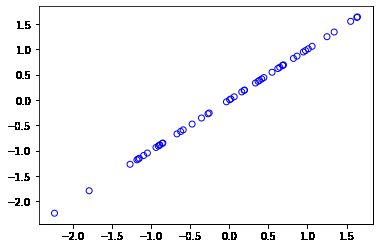
        为了帮助您理解PCA是如何工作的，您将首先从一个二维数据集开始，该数据集有一个大的变化方向和一个较小的变化方向。在这部分练习中，您将看到使用PCA将数据从2D减少到1D时会发生什么。

data = loadmat(r'E:\Code\ML\ml_learning\ex7-kmeans and PCA\data\ex7data1.mat')
X = data['X']
# facecolors 设置为空心 edgecolors边缘颜色
plt.scatter(X[:,0], X[:,1], facecolors='none', edgecolors='b')

 

2.2 实现PCA

        在这部练习中，将实现PCA算法，主成分分析包括两个计算步骤计算数据的协方差矩阵，接着使用奇异值分解计算特征向量U1,U2,U3...Un，这些对应数据中变化的主成分。

        但是在使用PCA之前，重要的是先对数据集中的数据进行标准化，使它们处于相同范围中。

def featureNormalize(X):
    """标准化"""
    
    means = X.mean(axis=0) # 按列
    stds = X.std(axis=0, ddof=1)
    X_norm = (X - means) / stds
    
    return X_norm, means, stds

        在对数据标准后，可以使用PCA计算主成分，但是首先需要计算数据的协方差矩阵，公式如下。

      

X是样本数据矩阵，m是样本个数，∑ 是一个n*n矩阵而非求和运算符。

        之后我们可以运用奇异值分解计算主成分，其中U包含主成分,每一列是我们数据要映射的向量，S包含对角矩阵，为奇异值。

def pca(X):
    sigma = (X.T @ X) / len(X)
    U, S, V = np.linalg.svd(sigma)
    
    return U, S, V

X_norm, means, stds = featureNormalize(X)
U, S, V = pca(X_norm)

# U = (array([[-0.70710678, -0.70710678],
#         [-0.70710678,  0.70710678]]),
# S = array([1.70081977, 0.25918023]),
# V =  array([[-0.70710678, -0.70710678],
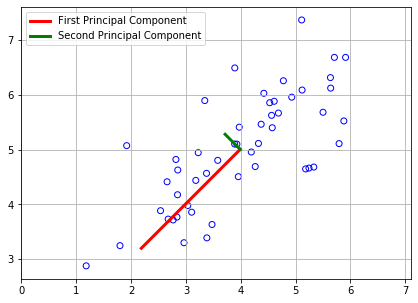
#         [-0.70710678,  0.70710678]]))

plt.figure(figsize=(7, 5))
plt.scatter(X[:,0], X[:,1], facecolors='none', edgecolors='b')
plt.plot([means[0], means[0] + 1.5*S[0]*U[0,0]], 
         [means[1], means[1] + 1.5*S[0]*U[0,1]],
        c='r', linewidth=3, label='First Principal Component')
plt.plot([means[0], means[0] + 1.5*S[1]*U[1,0]], 
         [means[1], means[1] + 1.5*S[1]*U[1,1]],
        c='g', linewidth=3, label='Second Principal Component')
plt.grid()
plt.axis("equal")  
plt.legend()

        在画图部分的代码，其实自己也还是没有怎么弄懂的，由于数学功底不足对于奇异值分解这部分，还没有怎么弄明白，只是知道U，V两向量是对数据做映射变化，S是放缩倍数。 

2.3  PCA降维

        在计算主成分之后，可以使用它们来减少数据集的特征维数。

2.3.1 将数据投影在主成分上

def projectData(X, U, K):
    Z = X @ U[:,:K]
    
    return Z
Z = projectData(X_norm, U, 1)
# Z[0] = array([1.48127391])

2.3.2 重构数据

def recoverData(Z, U, K):
    X_rec = Z @ U[:,:K].T
    
    return X_rec
X_rec = recoverData(Z, U, 1)
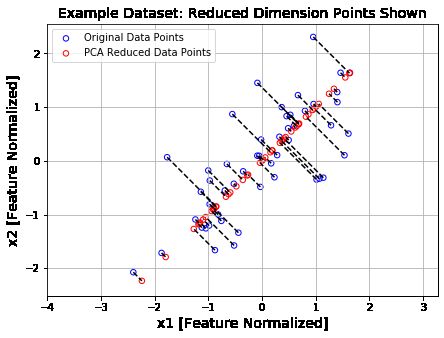
plt.scatter(X_rec[:,0], X_rec[:,1], facecolors='none', edgecolors='b')

2.3.3 可视化

plt.figure(figsize=(7,5))
plt.axis("equal") 
# 绘制散点图
plot = plt.scatter(X_norm[:,0], X_norm[:,1], s=30, facecolors='none', 
                   edgecolors='b',label='Original Data Points')
plot = plt.scatter(X_rec[:,0], X_rec[:,1], s=30, facecolors='none', 
                   edgecolors='r',label='PCA Reduced Data Points')

plt.title("Example Dataset: Reduced Dimension Points Shown",fontsize=14)
plt.xlabel('x1 [Feature Normalized]',fontsize=14)
plt.ylabel('x2 [Feature Normalized]',fontsize=14)
plt.grid(True)
# 加上连线
for x in range(X_norm.shape[0]):
    plt.plot([X_norm[x,0],X_rec[x,0]],[X_norm[x,1],X_rec[x,1]],'k--')
    # 输入第一项全是X坐标，第二项都是Y坐标
plt.legend()

2.4 人脸数据集

        在这部分练习中，将在人脸图像上运行PCA，以了解如何降维，首先先对数据可视化

data = loadmat(r'E:\Code\ML\ml_learning\ex7-kmeans and PCA\data\ex7faces.mat')
X = data['X']

def displayData(X, row, col):
    """可视化人脸"""
    fig, axs = plt.subplots(row, col, figsize=(8,8))
    for r in range(row):
        for c in range(col):
            axs[r][c].imshow(X[r*col + c].reshape(32,32).T, cmap = 'Greys_r')
            axs[r][c].set_xticks([])
            axs[r][c].set_yticks([])
displayData(X, 10, 10)

2.4.1 对人脸图像使用PCA

        为了在人脸数据集上运行PCA，我们首先通过从数据矩阵X中减去每个特征的平均值来规范化数据集。运行PCA后，将得到数据集的主成分。

X_norm, means, stds = featureNormalize(X)
U, S, V = pca(X_norm)
# 这里我们选取前36维
displayData(U[:,:36].T, 6, 6)

2.4.2 降维

        只将人脸数据集投射到前36个主成分上.

z = projectData(X_norm, U, K=36)
X_rec = recoverData(z, U, K=36)
displayData(X_rec, 10, 10)

参考文章 

吴恩达机器学习与深度学习作业目录 [图片已修复]