决策树（ID3,C4.5和CART）介绍、说明、联系和区别

决策树

1. 决策树介绍

决策树又称为判定树，是运用于分类的一种树结构。

决策树（decision tree）是一个树结构（可以是二叉树或非二叉树）。

每个非叶节点表示一个特征属性上的测试，
每个分支代表这个特征属性在某个值域上的输出，
每个叶节点存放一个类别。

使用决策树进行决策的过程就是从根节点开始，测试待分类项中相应的特征属性，并按照其值选择输出分支，直到到达叶子节点，将叶子节点存放的类别作为决策结果。

决策树学习的目标：根据给定的训练数据集构建一个决策树模型，使它能够对实例进行正确的分类。

决策树学习的本质：从训练集中归纳出一组分类规则，或者说是由训练数据集估计条件概率模型。

决策树学习的损失函数：正则化的极大似然函数

决策树学习的测试：最小化损失函数

决策树学习的目标：在损失函数的意义下，选择最优决策树的问题。

决策树原理和问答猜测结果游戏相似，根据一系列数据，然后给出游戏的答案。

2. 决策树构建过程

决策树学习的算法通常是一个递归地选择最优特征，并根据该特征对训练数据进行分割，使得各个子数据集有一个最好的分类的过程。这一过程对应着对特征空间的划分，也对应着决策树的构建。

1. 构建根节点，将所有训练数据都放在根节点，选择一个最优特征，按着这一特征将训练数据集分割成子集，使得各个子集有一个在当前条件下最好的分类。

2. 如果这些子集已经能够被基本正确分类，那么构建叶节点，并将这些子集分到所对应的叶节点去。

3. 如果还有子集不能够被正确的分类，那么就对这些子集选择新的最优特征，继续对其进行分割，构建相应的节点，如果递归进行，直至所有训练数据子集被基本正确的分类，或者没有合适的特征为止。

4. 每个子集都被分到叶节点上，即都有了明确的类，这样就生成了一颗决策树。

决策树的重点：通过属性构建节点

决策树的优点：

计算复杂度不高，
输出结果易于理解，
对中间值的缺失不敏感，
可以处理不相关特征数据。

决策树的缺点：

可能会产生过度匹配的问题（过拟合）

决策树预测过程：

收集数据：可以使用任何方法。
准备数据：收集完的数据，进行整理，将这些所有收集的信息按照一定规则整理出来，并排版，方便后续处理。
分析数据：可以使用任何方法，决策树构造完成之后，我们可以检查决策树图形是否符合预期。
训练算法：这个过程也就是构造决策树，同样也可以说是决策树学习，就是构造一个决策树的数据结构。
测试算法：使用经验树计算错误率。当错误率达到了可接收范围，这个决策树就可以投放使用了。
使用算法：此步骤可以使用适用于任何监督学习算法，而使用决策树可以更好地理解数据的内在含义。

2.1 属性选择

划分数据集的大原则是：将无序数据变得更加有序

在划分数据集前后信息发生的变化称为信息增益，获得信息增益最高的特征就是最好的选择(更好选择属性)。

如何计算信息增益？集合信息的度量方式称为香农熵，或者简称熵。

特征选择就是决定用哪个特征（属性）来划分特征空间。

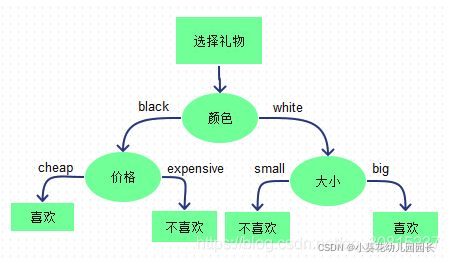
究竟选择哪个特征更好些？这就要求确定选择特征的准则

属性选择使用的度量方法：

• 熵
• 基尼

熵

熵定义为信息的期望值，如果待分类的事物可能划分在多个类之中，则符号$x_i$的信息定义为：
$$l(x_i)=-lo{g}_{2}p(x_i)$$

其中，$p(x_i)$是选择改分类的概率。

为了计算熵，我们需要计算所有类别所有可能值所包含的信息期望值，通过下式得到：
$$H=-\sum _{i=1}^{n}p(x_i)lo{g}_{2}p(x_i)$$

其中，n为分类数目，熵越大，随机变量的不确定性就越大。
(就是说熵越大，表示数据不纯，熵越小，纯度越高)

当熵中的概率由数据估计(特别是最大似然估计)得到时，所对应的熵称为经验熵(empirical entropy)

条件熵

信息增益表示得知特征X的信息而使得类Y的信息不确定性减少的程度。

条件熵H(Y∣X)表示在已知随机变量X的条件下随机变量Y的不确定性，随机变量X给定的条件下随机变量Y的条件熵(conditional entropy) H(Y|X)，定义X给定条件下Y的条件概率分布的熵对X的数学期望：

$$H(Y|X)=\sum _{i=1}^n{p}_{i}H(Y|X=x_i)$$

其中，$p_i=P(X=x_i)$

信息增益

信息增益是相对于特征而言的。所以，特征A对训练数据集D的信息增益g(D,A)，定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差，即：
$$g(D,A)=H(D)-H(D|A)$$

一般地，熵H(D)与条件熵H(D|A)之差成为互信息(mutual information)。决策树学习中的信息增益等价于训练数据集中类与特征的互信息。

信息增益比

特征A 对训练数据集D的信息增益比$g_R(D,A)$定义为其信息增益g(D,A)与训练数据集D的经验熵之比：
$$g_R(D,A)=\frac{g(D,A)}{H(D)}$$

3. 决策树生成和修建

决策树生成算法递归地产生决策树，直到不能继续下去未为止。这样产生的树往往对训练数据的分类很准确，但对未知的测试数据的分类却没有那么准确，即出现过拟合现象。

过拟合的原因在于学习时过多地考虑如何提高对训练数据的正确分类，从而构建出过于复杂的决策树。

解决这个问题的办法是考虑决策树的复杂度，对已生成的决策树进行简化。

4. 决策树常见算法

ID3

ID3算法是由Ross Quinlan提出的决策树的一种算法实现，以信息论为基础，以信息熵和信息增益为衡量标准，从而实现对数据的归纳分类。

越是小型的决策树越优于大的决策树

具体方法：

从根结点(root node)开始，对结点计算所有可能的特征的信息增益，选择信息增益最大的特征作为结点的特征。

由该特征的不同取值建立子节点，再对子结点递归地调用以上方法，构建决策树；直到所有特征的信息增益均很小或没有特征可以选择为止；

最后得到一个决策树。

缺点：

没有剪枝过程，为了去除过渡数据匹配的问题，可通过裁剪合并相邻的无法产生大量信息增益的叶子节点;

信息增益的方法偏向选择具有大量值的属性，也就是说某个属性特征索取的不同值越多，那么越有可能作为分裂属性，这样是不合理的；

只可以处理离散分布的数据特征

C4.5

与ID3算法相似，但是做了改进，将信息增益比作为选择特征的标准。

CART（基尼指数）

CART，又名分类回归树，是在ID3的基础上进行优化的决策树，学习CART记住以下几个关键点：

1. CART既能是分类树，又能是回归树；

2. 当CART是分类树时，采用GINI值作为节点分裂的依据；当CART是回归树时，采用样本的最小方差作为节点分裂的依据；

3. CART是一棵二叉树

定义：基尼指数（基尼不纯度）：表示在样本集合中一个随机选中的样本被分错的概率。

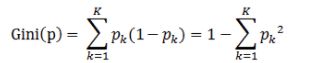
注意：Gini指数越小表示集合中被选中的样本被分错的概率越小，也就是说集合的纯度越高，反之，集合越不纯。

5.总结

决策树（有监督算法，概率算法）

1. 只接受离散特征，属于分类决策树。
2. 条件熵的计算 H(Label |某个特征) 这个条件熵反映了在知道该特征时，标签的混乱程度，可以帮助我们选择特征，选择下一步的决策树的节点。
3. Gini和entropy（熵）的效果没有大的差别，在scikit learn中默认用Gini是因为Gini指数不需要求对数，计算量少。
4. 把熵用到了集合上，把集合看成随机变量。
5. 决策树：贪心算法，无法从全局的观点来观察决策树，从而难以调优。
6. 叶子节点上的最小样本数，太少，缺乏统计意义。从叶子节点的情况，可以看出决策树的质量，发现有问题也束手无策。
7. 优点：可解释性强，可视化。
8. 缺点：容易过拟合（通过剪枝避免过拟合），很难调优，准确率不高
9. 二分类，正负样本数目相差是否悬殊，投票机制
10. 决策树算法可以看成是把多个逻辑回归算法集成起来。

ID3、C4.5、CART的区别

ID3 使用信息增益作为选择特征的准则；
C4.5 使用信息增益比作为选择特征的准则；
CART 使用 Gini 指数作为选择特征的准则

ID3:
熵表示的是数据中包含的信息量大小。熵越小，数据的纯度越高，也就是说数据越趋于一致，这是我们希望的划分之后每个子节点的样子。

信息增益 = 划分前熵 - 划分后熵。信息增益越大，则意味着使用属性 a 来进行划分所获得的 “纯度提升” 越大 **。也就是说，用属性 a 来划分训练集，得到的结果中纯度比较高。

ID3 仅仅适用于二分类问题。ID3 仅仅能够处理离散属性。

C4.5:

C4.5 克服了 ID3 仅仅能够处理离散属性的问题，以及信息增益偏向选择取值较多特征的问题，使用信息增益比来选择特征。

信息增益比 = 信息增益 / 划分前熵 .选择信息增益比最大的作为最优特征。

C4.5 处理连续特征是先将特征取值排序，以连续两个值中间值作为划分标准。尝试每一种划分，并计算修正后的信息增益，选择信息增益最大的分裂点作为该属性的分裂点。

CART:

CART 与 ID3，C4.5 不同之处在于 CART 生成的树必须是二叉树。也就是说，无论是回归还是分类问题，无论特征是离散的还是连续的，无论属性取值有多个还是两个，内部节点只能根据属性值进行二分。

CART 的全称是分类与回归树。从这个名字中就应该知道，CART 既可以用于分类问题，也可以用于回归问题。

回归树中，使用平方误差最小化准则来选择特征并进行划分。每一个叶子节点给出的预测值，是划分到该叶子节点的所有样本目标值的均值，这样只是在给定划分的情况下最小化了平方误差。

要确定最优化分，还需要遍历所有属性，以及其所有的取值来分别尝试划分并计算在此种划分情况下的最小平方误差，选取最小的作为此次划分的依据。由于回归树生成使用平方误差最小化准则，所以又叫做最小二乘回归树。

分类树种，使用 Gini 指数最小化准则来选择特征并进行划分；

Gini 指数 vs 熵

既然这两个都可以表示数据的不确定性，不纯度。那么这两个有什么区别那？

• Gini 指数的计算不需要对数运算，更加高效；
• Gini 指数更偏向于连续属性，熵更偏向于离散属性。