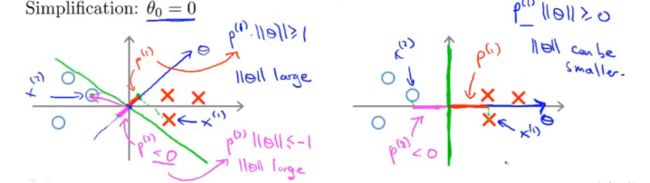机器学习基础----基于吴恩达机器学习课程的笔记
写在前面:本篇笔记是对于机器学习课程及其体系的简单梳理,方便以后的查找,涉及的原理解释较少,一些算法的实现和优化待日后补充。
机器学习基础
文章目录
- 机器学习基础
-
- 一、监督学习 与 无监督学习
- 二、回归问题
-
- 一、函数模型----线性回归
- 二、算法模型
-
- (一)梯度下降算法
- (二)正规方程法
- 三、分类问题
-
- 先从二分类开始(0或1):
-
- 一、函数模型----Logistic回归
- 二、算法模型
-
- (一)梯度下降算法
- 多分类:
- 四、过拟合的问题
-
- 一、介绍
- 二、解决方法之----正则化
-
- (一)线性回归函数
- (二)Logistic函数
- 五、神经网络
-
- 一、为什么要用神经网络
- 二、主要思想
- 三、激活函数
- 四、代价函数
- 五、反向传播
- 六、向量化
- 七、随机初始化
- 六、算法评估
-
- 一、分割数据集
-
- (一)分为两类
- (二)分为三类
- 二、高偏差与高方差(欠拟合与过拟合)
- 三、学习曲线
-
- (一)高偏差
- (二)高方差
- 四、以上的总结
- 五、误差分析
-
- (一)查准率与召回率
- 七、SVM
-
- 一、优化目标函数
- 二、大间隔分类器
- 三、核函数
- 八、聚类算法
-
- 一、K-Means算法
-
- (一)主要原理
- (二)优化目标函数
- (三)随机初始化
- (四)K的选取
- 二、降维问题
-
- (一)压缩数据
- (二)可视化数据
- 三、主成分分析(PCA)算法
-
- (一)主要思想
- (二)低维平面的计算
- (三)参数K值的选取
- 三、异常检测
-
- (一)算法
- (二)算法评估
- (三)异常检测与监督学习
- (四)多元高斯分布
- 九、推荐系统
-
- 一、基于内容的推荐算法
- 二、协同过滤
- 三、推荐
- 四、均值归一化
- 十、处理大数据集的算法
-
- 一、随机梯度下降
- 二、Mini-batch梯度下降
- 三、 MapReduce
一、监督学习 与 无监督学习
- 监督学习 :给定数据集及其特征,预测未知量的正确答案。
- 主要有回归问题和分类问题
- 无监督学习 :给定数据集但不提供特征,由算法寻找其中的结构。
- 聚类问题
二、回归问题
一、函数模型----线性回归
-
假设函数
h ( θ ) = ∑ j = 0 n θ i x i , ( x 0 = 1 ) h(\theta)=\sum_{j=0}^n \theta_i x_i,(x_0=1) h(θ)=j=0∑nθixi,(x0=1) -
代价函数
J ( θ ) = 1 2 m ∑ i = 0 m ( y i − h θ ( x i ) ) 2 , x i 表 示 第 i 个 样 本 的 特 征 值 构 成 的 向 量 J(\theta) = \frac{1}{2m} \sum_{i=0}^m (y_i-h_\theta (x^i))^2,\\x^i表示第i个样本的特征值构成的向量 J(θ)=2m1i=0∑m(yi−hθ(xi))2,xi表示第i个样本的特征值构成的向量
回归函数若出现了x的几次方等,可以用变量代换,最终函数依然可以是一个线性回归函数。
二、算法模型
(一)梯度下降算法
-
主要思想
取一点,寻找下降最快的方向(即梯度),更新点的位置;之后重复以上步骤,知道函数值收敛,这一值即为局部最小。
θ i = θ i − α ∂ J ( θ ) ∂ θ i = θ i − α m ∑ i = 0 m ( h θ ( x i ) − y i ) x i , α 表 示 学 习 率 \theta_i=\theta_i-\alpha\frac{\partial J(\theta)}{\partial\theta_i}=\theta_i-\frac{\alpha}{m} \sum_{i=0}^m (h_\theta(x^i)-y^i)x^i,\alpha表示学习率 θi=θi−α∂θi∂J(θ)=θi−mαi=0∑m(hθ(xi)−yi)xi,α表示学习率
线性回归的代价函数是凸函数,所以局部最小就是全局最小
-
实用处理技巧
(1)特征缩放
不同特征的取值如果相差过大(数量级的比较),会造成代价函数过于倾向某一方或者某几方,梯度下降找到最优解需要耗费更长的时间。
为此,将特征值进行缩放,使其值在相同的范围(或数量级)内,可以加快梯度下降的速度。
一种特征缩放的方法:均值归一化
x i = x i − μ i s i , s i 为 x i 的 范 围 x_i=\frac{x_i-\mu_i}{s_i},s_i为x_i的范围 xi=sixi−μi,si为xi的范围(2)学习率的选择
- 太小,可以精确地使得到代价函数达到最小值,但是需要迭代很多次,时间代价大。
- 太大,代价函数每次迭代可能不会下降,也可能找不到精确的最小值。
需要根据实际情况调试学习率。
对于大数据样本,一种有效的方法是刚开始选择大学习率,随着迭代逐渐减小学习率。
-
代码实现
待补充
(二)正规方程法
-
主要思想
对 J(θ) 的每一个 θ 求偏导,另偏导之后的式子等于0;联立所有的偏导式,求解出所有 θ 的值。
令 X = [ 1 x 1 1 x 2 1 . . . . . . x n 1 1 x 1 2 x 2 2 . . . . . . x n 2 . . . . . . . . . . . . . . . . . . 1 x 1 m x 2 m . . . . . . x n m ] 令 Y = [ y 1 y 2 . . . y n ] 则 θ = ( X T X ) − 1 X T Y 即 为 使 J ( θ ) 最 小 的 θ 矩 阵 令X=\begin{bmatrix} 1 & x^1_1 & x^1_2 & ...... & x^1_n\\ 1 & x^2_1 & x^2_2 & ...... & x^2_n\\ ... & ... & ... & ...... & ...\\ 1 & x^m_1 & x^m_2 & ...... & x^m_n \end{bmatrix}\\ 令Y=\begin{bmatrix} y_1\\y_2\\...\\y_n \end{bmatrix}\\ 则\theta =(X^TX)^{-1}X^TY即为使J(\theta)最小的\theta矩阵 令X=⎣⎢⎢⎡11...1x11x12...x1mx21x22...x2m........................xn1xn2...xnm⎦⎥⎥⎤令Y=⎣⎢⎢⎡y1y2...yn⎦⎥⎥⎤则θ=(XTX)−1XTY即为使J(θ)最小的θ矩阵 -
与梯度下降算法的比较
梯度下降算法:
-
需要选择合适的学习率;
-
需要迭代很多次;
-
当n很大时耗费的时间可能比正规方程少。
正规方程法:
- 只需要计算矩阵;
- 矩阵计算需要的时间~O(n³),当n很大时需要耗费很长时间;
- XTX 可能不可逆,需要对特征进行相应处理。
-
-
代码实现
待补充
P(25-30)
三、分类问题
先从二分类开始(0或1):
一、函数模型----Logistic回归
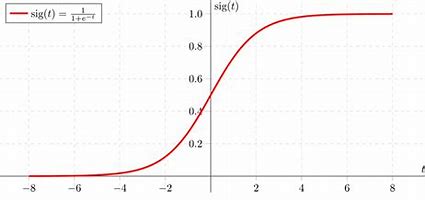
- Sigmoid函数
g ( z ) = 1 1 + e − z g(z)=\frac{1}{1+e^{-z}} g(z)=1+e−z1
-
假设函数
h θ ( x ) = g ( θ T x ) h_\theta(x)=g(\theta^Tx) hθ(x)=g(θTx)这里的假设函数是指当给定参数θ和特征向量x时,y为某一个离散值(某一类)时的概率。
-
决策界限
通过sigmoid函数可以看出,决策界限为:
θ T x = 0 \theta^Tx=0 θTx=0 -
代价函数
C o s t ( h θ ( x ) , y ) = { − l o g ( h θ ( x ) ) , y = 1 − l o g ( 1 − h θ ( x ) ) , y = 0 = − y l o g ( h θ ( x ) ) − ( 1 − y ) l o g ( 1 − h θ ( x ) ) J ( θ ) = 1 m ∑ i = 0 m C o s t ( h θ ( x i ) , y i ) = − 1 m ∑ i = 0 m [ y l o g ( h θ ( x ) ) + ( 1 − y ) l o g ( 1 − h θ ( x ) ) ] Cost(h_\theta(x),y)=\left\{ \begin{aligned} -log(h_\theta(x)),y=1\\ -log(1-h_\theta(x)),y=0 \end{aligned} \right.=-ylog(h_\theta(x))-(1-y)log(1-h_\theta(x))\\ J(\theta)=\frac{1}{m}\sum_{i=0}^m Cost(h_\theta(x^i),y^i)=-\frac{1}{m}\sum_{i=0}^m [ylog(h_\theta(x))+(1-y)log(1-h_\theta(x))] Cost(hθ(x),y)={−log(hθ(x)),y=1−log(1−hθ(x)),y=0=−ylog(hθ(x))−(1−y)log(1−hθ(x))J(θ)=m1i=0∑mCost(hθ(xi),yi)=−m1i=0∑m[ylog(hθ(x))+(1−y)log(1−hθ(x))]
若使用线性回归函数的代价函数,会带来很多局部最小值;使用这里的代价函数,就会使其为凸函数,只有整体最小值。
这里的代价函数是通过极大似然法得来的
二、算法模型
(一)梯度下降算法
-
主要思想
与线性回归函数的思路一致,且θ更新后的表达式也一致;
不同点是假设函数h(θ)不同。
θ i = θ i − α ∂ J ( θ ) ∂ θ i = θ i − α m ∑ i = 0 m ( h θ ( x i ) − y i ) x i \theta_i=\theta_i-\alpha\frac{\partial J(\theta)}{\partial\theta_i}=\theta_i-\frac{\alpha}{m} \sum_{i=0}^m (h_\theta(x^i)-y^i)x^i θi=θi−α∂θi∂J(θ)=θi−mαi=0∑m(hθ(xi)−yi)xi
-
优化算法
待补充
P(36、37)
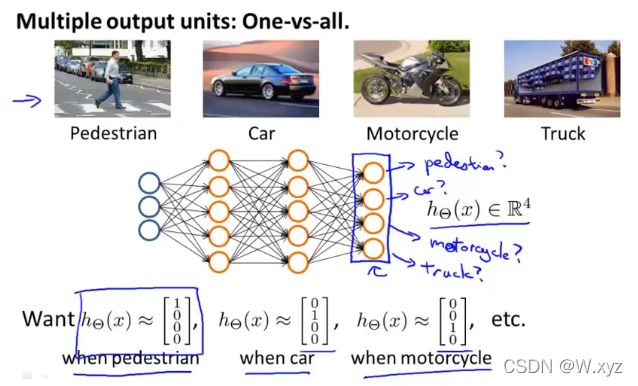
多分类:
先挑出一类来,再将其他的类看成一类,这样就转化为了二分类的问题;接着对每一类都重复上面的步骤。
四、过拟合的问题
一、介绍
几乎能拟合所有数据以至于不能很好地泛化,使得预测值不准确。
过拟合常见的一种原因是变量(特征)过多而训练数据(样本)太少。
相对应就会有两个解决办法:
- 减少变量的数量,选取较为重要的变量----但是舍弃一些变量的同时也舍弃了一些问题的信息,它们可能对问题都有用;
- 正则化:保留所有的变量但减小量级。
二、解决方法之----正则化
(一)线性回归函数
- 原理
J ( θ ) = 1 2 m [ ∑ i = 0 m ( y i − h θ ( x i ) ) 2 + λ ∑ j = 1 n θ j 2 ] J(\theta) = \frac{1}{2m} [\sum_{i=0}^m (y_i-h_\theta (x^i))^2+\lambda \sum_{j=1}^n \theta_j^2] J(θ)=2m1[i=0∑m(yi−hθ(xi))2+λj=1∑nθj2]
λ用来控制(平衡)两个目标之间的取舍:
- 第一个目标是代价函数里的第一项,拟合数据的准确度;
- 第二个目标是代价函数的第二项,尽量将参数控制得更小,从而保证假设函数模型的相对简单。(高阶项前面的参数小,则它对函数整体的影响就比较小,因此函数不会那么“弯弯扭扭”,即函数模型相对简单);也可以理解成是对 θ 的惩罚。
λ 决定了我们是更关心第一项的优化还是更关心第二项的优化。
-
对于梯度下降算法
θ i = θ i − α ∂ J ( θ ) ∂ θ i = ( 1 − α λ m ) θ i − α m ∑ i = 0 m ( h θ ( x i ) − y i ) x i \theta_i=\theta_i-\alpha\frac{\partial J(\theta)}{\partial\theta_i}=(1-\alpha \frac{\lambda}{m})\theta_i-\frac{\alpha}{m} \sum_{i=0}^m (h_\theta(x^i)-y^i)x^i θi=θi−α∂θi∂J(θ)=(1−αmλ)θi−mαi=0∑m(hθ(xi)−yi)xi
每次迭代都会先使θ变小一点在减去后面的第二项,一定程度上解释了上面的对于参数控制的原理。 -
对于正规方程法
θ = ( X T X + λ [ 0 1 1 . . . 1 ] ) − 1 X T Y \theta =(X^TX+\lambda\begin{bmatrix} 0 \\ & 1 \\ & & 1 & \\ & & & ... \\ & & & & 1 \end{bmatrix})^{-1}X^TY θ=(XTX+λ⎣⎢⎢⎢⎢⎡011...1⎦⎥⎥⎥⎥⎤)−1XTY
(二)Logistic函数
-
原理
与线性回归原理一样:
J ( θ ) = − 1 m ∑ i = 0 m [ y l o g ( h θ ( x ) ) + ( 1 − y ) l o g ( 1 − h θ ( x ) ) ] + λ 2 m ∑ j = 1 n θ j 2 J(\theta) =-\frac{1}{m}\sum_{i=0}^m [ylog(h_\theta(x))+(1-y)log(1-h_\theta(x))]+\frac{\lambda}{2m} \sum_{j=1}^n \theta_j^2 J(θ)=−m1i=0∑m[ylog(hθ(x))+(1−y)log(1−hθ(x))]+2mλj=1∑nθj2θ i = θ i − α ∂ J ( θ ) ∂ θ i = ( 1 − α λ m ) θ i − α m ∑ i = 0 m ( h θ ( x i ) − y i ) x i \theta_i=\theta_i-\alpha\frac{\partial J(\theta)}{\partial\theta_i}=(1-\alpha \frac{\lambda}{m})\theta_i-\frac{\alpha}{m} \sum_{i=0}^m (h_\theta(x^i)-y^i)x^i θi=θi−α∂θi∂J(θ)=(1−αmλ)θi−mαi=0∑m(hθ(xi)−yi)xi
-
优化算法
待补充
五、神经网络
一、为什么要用神经网络
当特征值n很大的时候,对于分类问题中的(θ^T)X,会有一次项、二次项、三次项等等,这导致需要求解的θ参数很多。
假设n=2500,且只有二次项,则一共需要求解的参数量为:
C 2500 2 + 2500 = 3126250 , 数 量 级 为 n 2 C_{2500}^2+2500=3126250,数量级为n^2 C25002+2500=3126250,数量级为n2
二、主要思想
提出一种假设:大脑处理各种各样的事情,并不需要成千上万的“程序”,只需要一个学习算法。
神经网络的主要思想即是上面这种假设。
从原始特征出发(可以是特征本身也可以是特征的组合等),通过加权和函数计算等学习挖掘出一层层更加有效的特征,以此得到更好的假设函数。
输入层---->隐藏层---->输出层
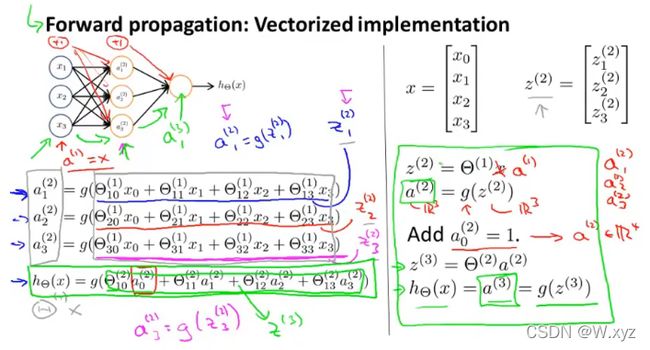
一个简单的例子:
首先利用前向传播一步步地计算出每一层相应的值,缓存一些需要的值,一直到最后出 y(不是预测的0或1而是概率);然后再进行反向传播,一步步地往前计算有关导数,最后算到第一层的参数矩阵相关的导数,接着利用梯度下降更新参数矩阵。这样一次次地迭代下去。
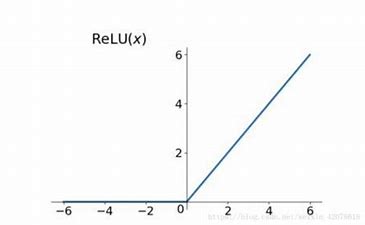
三、激活函数
上图中的g(z)即为激活函数,不同层可以使用不同的激活函数。
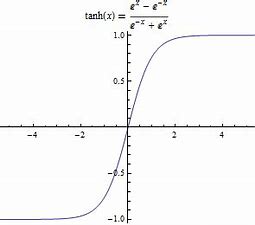
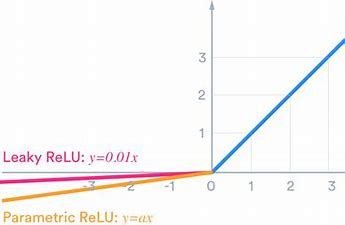
一些激活函数:
四、代价函数
若使用sigmoid作为激活函数,则与逻辑回归的代价函数思想一样,只不过在多分类中输出层不止一个单元,如下:
J ( θ ) = − 1 m ∑ i = 0 m ∑ k = 1 K [ y i l o g ( h θ ( x i ) ) + ( 1 − y i ) l o g ( 1 − h θ ( x i ) ) ] + λ 2 m ∑ l = 1 L − 1 ∑ i = 1 S l ∑ j = 1 S l + 1 ( θ j i l ) 2 K 为 输 出 层 单 元 个 数 , L 代 表 层 数 J(\theta) =-\frac{1}{m}\sum_{i=0}^m \sum_{k=1}^K [y^ilog(h_\theta(x^i))+(1-y^i)log(1-h_\theta(x^i))]+\frac{\lambda}{2m} \sum_{l=1}^{L-1} \sum_{i=1}^{S_l}\sum_{j=1}^{S_{l+1}} (\theta_{ji}^l)^2\\ K为输出层单元个数,L代表层数 J(θ)=−m1i=0∑mk=1∑K[yilog(hθ(xi))+(1−yi)log(1−hθ(xi))]+2mλl=1∑L−1i=1∑Slj=1∑Sl+1(θjil)2K为输出层单元个数,L代表层数
五、反向传播
核心思想是链式法则向前求导
误差值:
δ j l = a j l − y j \delta^l_j=a^l_j-y_j δjl=ajl−yj
以 单 个 样 本 和 s i g m o i d 作 为 激 活 函 数 为 例 介 绍 反 向 传 播 算 法 的 思 想 : 设 z = θ T x , a = g ( z ) ; ∂ J ∂ a = − y a + 1 − y 1 − a ∂ J ∂ z = ∂ J ∂ a ∂ a ∂ z = a − y ∂ J ∂ θ = ∂ J ∂ z ∂ z ∂ θ 上 面 是 最 后 一 层 的 反 向 传 播 求 导 , 前 面 的 层 级 则 根 据 链 式 法 则 继 续 用 代 价 函 数 求 相 应 的 偏 导 运 算 时 使 用 向 量 化 进 行 运 算 , 多 个 进 行 累 加 即 可 以单个样本和sigmoid作为激活函数为例介绍反向传播算法的思想: \\设z=\theta^Tx,a=g(z);\\ \\ \frac{\partial J}{\partial a}=-\frac{y}{a}+\frac{1-y}{1-a}\\ \\ \frac{\partial J}{\partial z}=\frac{\partial J}{\partial a}\frac{\partial a}{\partial z}=a-y\\ \\ \frac{\partial J}{\partial \theta}=\frac{\partial J}{\partial z}\frac{\partial z}{\partial \theta}\\ 上面是最后一层的反向传播求导,前面的层级则根据链式法则继续用代价函数求相应的偏导 \\运算时使用向量化进行运算,多个进行累加即可 以单个样本和sigmoid作为激活函数为例介绍反向传播算法的思想:设z=θTx,a=g(z);∂a∂J=−ay+1−a1−y∂z∂J=∂a∂J∂z∂a=a−y∂θ∂J=∂z∂J∂θ∂z上面是最后一层的反向传播求导,前面的层级则根据链式法则继续用代价函数求相应的偏导运算时使用向量化进行运算,多个进行累加即可
六、向量化
避免使用 for 循环,而是直接将一组数据看作是一个向量矩阵,直接对这些向量进行运算,可以大大加快运算速度。
对于一个样本,有特征值矩阵、参数矩阵、激活值函数矩阵等等;
多个样本,则可以把以上每一项的矩阵联立成维数更大的矩阵。
- 向量化要注意矩阵维度的问题,而且还可以作为检验是否有bug的方法
- 向量化运算特别是乘积的时候,可能会需要转置矩阵
七、随机初始化
六、算法评估
一、分割数据集
(一)分为两类
一般按照7:3的比例将数据集分为训练集和测试集(随机性)。利用训练集求出参数 θ,之后用测试集计算代价函数 J(θ) ,即测试误差 。
对于逻辑回归,还有一种测试误差的计算方法:错误分类
e r r ( h θ ( x ) , y ) = { 1 , h θ ( x ) ≥ 0.5 、 y = 0 o r h θ ( x ) < 0.5 、 y = 1 0 , o t h e r w i s e err(h_\theta(x),y)=\left\{ \begin{aligned} 1, h_\theta(x)\geq0.5、y=0\quad or\quad h_\theta(x)<0.5、y=1\\ 0,otherwise \end{aligned} \right. err(hθ(x),y)={1,hθ(x)≥0.5、y=0orhθ(x)<0.5、y=10,otherwise
(二)分为三类
对于模型选择问题:
一般按照6:2:2的比例将数据集分为训练集、交叉验证集和测试集。在不同的函数模型下用训练集求解出不同的假设函数,然后用验证集分别计算每一个模型的代价函数值(不考虑正则化项的代价函数,因为正则化和验证集是两种选择模型的方法),比较每一组代价函数值的大小从而选出最好的假设函数。最后就可以用测试集的代价函数值来估计模型的泛化误差。
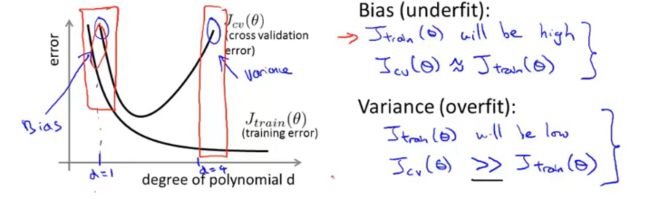
二、高偏差与高方差(欠拟合与过拟合)
一般而言,多项式的次数比较小的时候会出现欠拟合,比较大的时候会出现过拟合。用训练误差和验证误差图(较为简单的例子)表示如下:
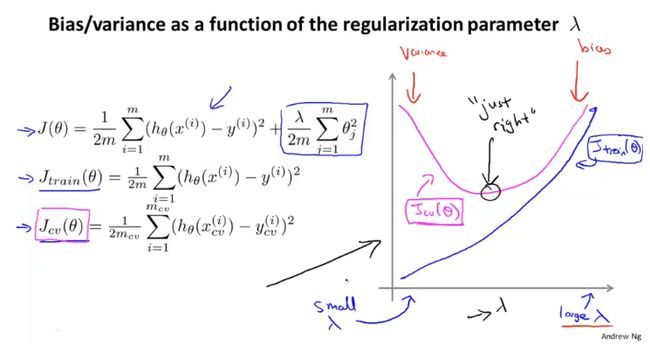
在使用正则化解决过拟合的问题,求解假设函数时,可以一步步对 λ 进行调参,求出相应的假设函数;然后在验证集上计算不含正则项的代价函数,以此求出最佳的 λ 值;最后将其放入测试集中计算泛化误差。(一个简单的例子如下图)
三、学习曲线
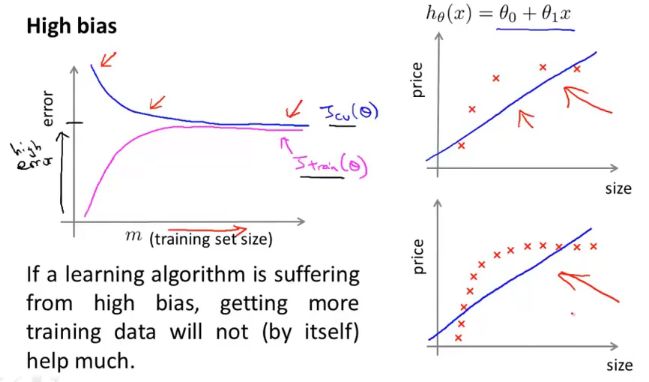
(一)高偏差
高偏差学习曲线大致如下图所示(理想化):
当训练集很大时,可以看到验证误差和训练误差几乎持平。所以,如果我们的算法处于高偏差,那么加入更多的训练集数据对改善算法的表现实际上没有多大的效果。
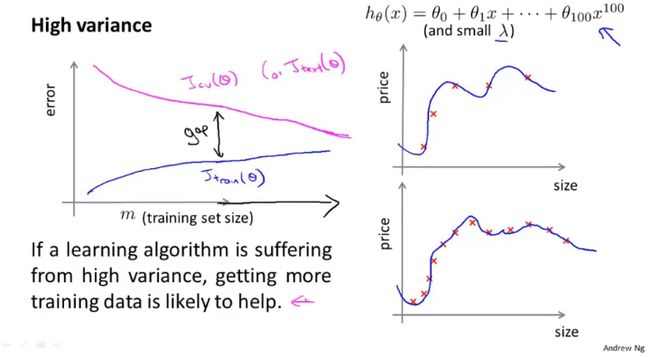
(二)高方差
高方差学习曲线大致如下图所示(理想化):
刚开始验证误差和训练误差相差很大,但当训练集很大时,验证误差和训练误差的相差会逐渐减少。所以,如果我们的算法处于高方差,那么加入更多的训练集数据对改善算法的表现有一定的帮助。
四、以上的总结
学习算法有高方差:
- 增加训练集数量
- 选用更少的特征
- 增大 λ
学习算法有高偏差:
- 选用更多的特征
- 增加多项式特征(实质上就是增加了特征(的组合))
- 减小 λ
选择较简单的神经网络结构容易出现欠拟合,但是计算量小;
较复杂的神经网络性能更好,容易出现过拟合,可以用正则化来修正,但是计算量比较大;
对于神经网络隐藏层数的选择,可以利用上面的分为三类的方法来进行评估。
五、误差分析
在设计机器学习算法系统的时候,可以先设计一个较简单的算法,然后应用该算法,分析其存在的错误,之后就可决定改进方向。可以加入一个数值评价指标,当决定如何改进算法时,将改进后应用算法得到的指标与改进前相比,观察此次改进是否可以提高算法的表现。
(一)查准率与召回率
对于偏斜类的问题:
比如在一个二分类问题中,几乎所有的数据都是一个类别(下面以99.5:0.5为例)。我们设计的算法应用上去错误率(一个数值评价指标)可能是1%,而如果我们全都将其认为是一个类别(这样就不是一个机器学习算法了),它的错误率就只有0.5%。但是,这样改进的话并不能说是提高了模型的质量,因为明显全部看成一类的方法并不是一个好的分类模型。
于是引入查准率(预测的准确性)与召回率(正确预测的与实际的契合度):
查 准 率 = 某 一 类 预 测 正 确 的 数 量 / 对 于 该 类 预 测 的 数 量 召 回 率 = 某 一 类 预 测 正 确 的 数 量 / 实 际 上 该 类 的 数 量 查准率=某一类预测正确的数量/对于该类预测的数量\\ \\ 召回率=某一类预测正确的数量/实际上该类的数量 查准率=某一类预测正确的数量/对于该类预测的数量召回率=某一类预测正确的数量/实际上该类的数量
假设我们将上面的 h(x) 临界值设为 0.8 ,即在概率高于0.8时才预测为 1 ,则此算法具有高查准率与低召回率 ;设为 0.2 则相反。
看到一种比较生动的解释:
- 查准:宁可放过一百也不错杀一个
- 召回:宁可错杀一百也不放过一个
查准率与召回率的权衡:比较F值的大小
F = 2 P R P + R F=2\frac{PR}{P+R} F=2P+RPR
实际上还有其他值用来权衡两者,这里的 F值 是较为常用的一种
七、SVM
一、优化目标函数
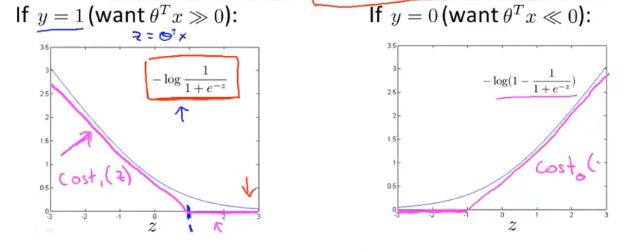
C ∑ i = 1 m [ y i c o s t 1 ( θ T x i ) + ( 1 − y i ) c o s t 0 ( θ T x i ) ] + 1 2 ∑ i = 1 n θ j 2 C\sum_{i=1}^m[y^icost_1(\theta^Tx^i)+(1-y^i)cost_0(\theta^Tx^i)]+\frac{1}{2}\sum_{i=1}^n\theta_j^2 Ci=1∑m[yicost1(θTxi)+(1−yi)cost0(θTxi)]+21i=1∑nθj2
其中,cost函数为logistic代价函数里log的变形,如下所示:
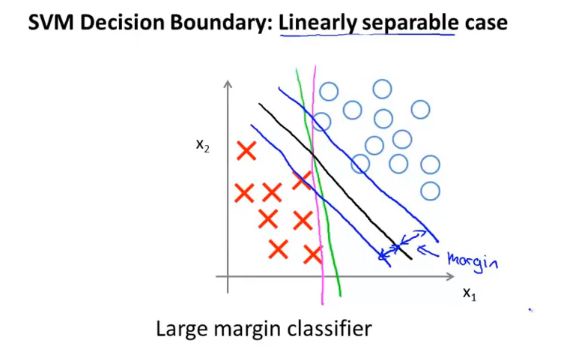
二、大间隔分类器
如下图的黑线,即为SVM大间隔分类器的表现:
SVM表现为大间隔分类器的原理:
假设我们的SVM决策边界为:
θ T x ≥ 1 θ T x ≤ − 1 \theta^Tx≥1\\ \theta^Tx≤-1 θTx≥1θTx≤−1
不等式左边在坐标系中的本质是 θ 与 x 的点乘,x在θ方向上的投影与θ长度的乘积,因此要=1或-1,就得使决策边界与数据点有一定的距离。
三、核函数
下面以举例的方式简单介绍SVM中的核函数:
在一些问题中我们需要拟合非线性的判别边界,因此会有很多复杂的高阶多项式特征。使用核函数定义新特征 f1 , f2 , f3 , … 代替高阶项,或是找到更好的特征来更优地找出判别边界。
-
选取标记点 l1 , l2 , l3 … (可选为训练样本点)
-
将新特征 f1 , f2 , f3 , … 定义为与样本 x1 , x2 , … 与标记点相似度的度量。
-
选取相似度函数,这样的相似度函数即核函数。
一种核函数:高斯核函数
f = s i m i l a r i t y ( x , l ) = e − ( x − l ) 2 2 σ 2 f=similarity(x,l)=e^{-\frac{(x-l)^2}{2\sigma^2}} f=similarity(x,l)=e−2σ2(x−l)2 -
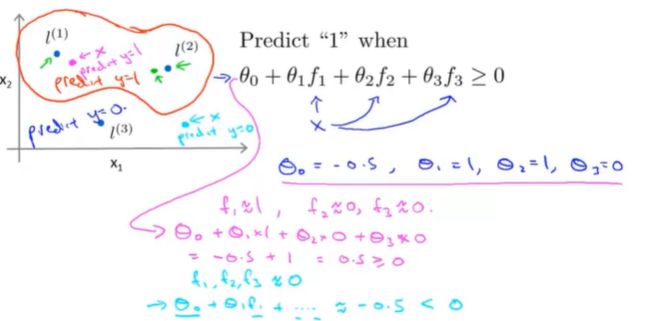
选用如上的高斯核函数,如下所示:
-
将计算好的 θ 参数与新特征 f 的值代入计算,得到预估值。
-
根据 θ 的不同就可得出决策边界,如上图接近 l1 ,l2 的预测为1,反之预测为0,橙红色的为决策边界。
八、聚类算法
一、K-Means算法
(一)主要原理
- 簇分配:随机初始化K个点为聚类中心(K为需要类别的数量);遍历每一个数据点,将其分配给最近的聚类中心,形成簇。
- 移动聚类中心:计算每一簇的中心点(取均值),将其作为新的聚类中心。
一次次迭代以上的步骤,直至聚类中心和簇都不在改变。
(二)优化目标函数
x i : 第 i 个 数 据 点 c i : x i 所 分 配 的 簇 μ k : 第 k 个 聚 类 中 心 J ( c 1 , . . . , c m , μ 1 , . . . , μ k ) = 1 m ∑ i = 1 m ( x i − μ c i ) 2 x^i:第i个数据点\\ c^i:x^i所分配的簇\\ \mu_k:第k个聚类中心\\ J(c^1,...,c^m,\mu_1,...,\mu_k)=\frac{1}{m}\sum_{i=1}^m(x^i-\mu_{c^i})^2 xi:第i个数据点ci:xi所分配的簇μk:第k个聚类中心J(c1,...,cm,μ1,...,μk)=m1i=1∑m(xi−μci)2
(三)随机初始化
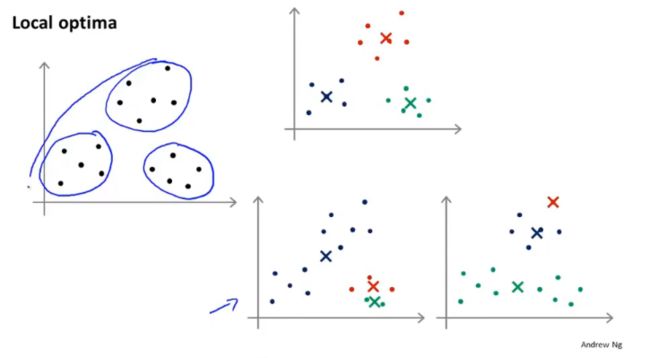
通常使用的方法是,随机挑选K个数据点当作初始聚类中心。但是可能会得到局部最优解,如下所示:
一种解决方法是多次随机初始化运行K-Means算法,选择其中优化目标函数最小的结果。
但是多次随机初始化只对K较小时避免局部最优有效;当K很大时,多次随机初始化不会有很大的改善。
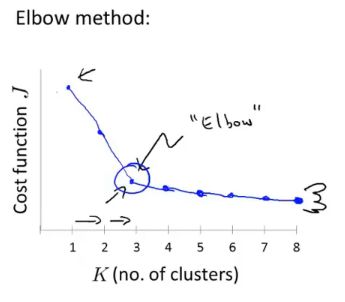
(四)K的选取
二、降维问题
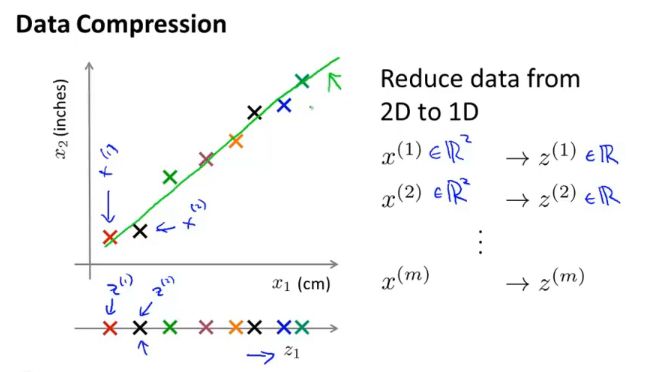
(一)压缩数据
对冗余的特征进行处理,使多个特征可以由一个特征表达出来,可以加快算法的运行速度。
比如在某个问题中,一个数据点是由两个特征表达的,但在由这两个特征构成的二维坐标系中,这些数据点近似在一条直线上,那么就可以以这条直线上的位置确定数据点,而不需要原来的两个特征了。
(二)可视化数据
三、主成分分析(PCA)算法
(一)主要思想
主要是对降维问题中压缩数据的算法。寻找一个比特征向量更低维的平面,将数据投影上去,使得数据点与投影点距离的平方和最小。
与线性回归的区别:
线性回归的目的是使代价函数最小化,用所有的x值来预测y,因此是y方向上距离的平方和最小;而PCA是将数据压缩,每一个特征都要考虑进去,因此是数据点与投影点距离的平方和最小。
(二)低维平面的计算
首先进行数据预处理,特征缩放(参考梯度下降算法中的实用处理技巧);之后进行以下计算:
S i g m a = 1 m ∑ i = 1 m x i ( x i ) T ( S i g m a 表 示 协 方 差 矩 阵 , x i 表 示 一 个 数 据 点 进 行 预 处 理 后 的 特 征 向 量 ) [ U , S , V ] = s v d ( S i g m a ) s v d 为 奇 异 值 分 解 , 得 到 三 个 矩 阵 取 其 中 U 矩 阵 的 前 K 列 ( 假 设 需 要 K 维 平 面 ) 作 为 新 矩 阵 U r e d u c e , 该 矩 阵 即 为 低 维 平 面 的 矩 阵 Z i = ( U r e d u c e ) T x i , 即 为 在 低 维 平 面 上 x i 对 应 的 坐 标 Sigma=\frac{1}{m}\sum_{i=1}^mx^i(x^i)^T\\ (Sigma表示协方差矩阵,x^i表示一个数据点进行预处理后的特征向量)\\ [U,S,V]=svd(Sigma)\\ svd为奇异值分解,得到三个矩阵\\ 取其中U矩阵的前K列(假设需要K维平面)作为新矩阵U_{reduce},该矩阵即为低维平面的矩阵\\ \\ Z^i=(U_{reduce})^Tx^i,即为在低维平面上x^i对应的坐标 Sigma=m1i=1∑mxi(xi)T(Sigma表示协方差矩阵,xi表示一个数据点进行预处理后的特征向量)[U,S,V]=svd(Sigma)svd为奇异值分解,得到三个矩阵取其中U矩阵的前K列(假设需要K维平面)作为新矩阵Ureduce,该矩阵即为低维平面的矩阵Zi=(Ureduce)Txi,即为在低维平面上xi对应的坐标
(三)参数K值的选取
上面奇异值分解得到的S矩阵是一个对角矩阵,K值的选取满足以下条件:
∑ i = 1 k S i i ∑ i = 1 m S i i ≥ 0.99 , ( 0.99 可 变 ) 保 留 了 99 % 的 方 差 性 \frac{\sum_{i=1}^kS_{ii}}{\sum_{i=1}^mS_{ii}}≥0.99,(0.99可变)\\ 保留了99%的方差性 ∑i=1mSii∑i=1kSii≥0.99,(0.99可变)保留了99%的方差性
注意:使用PCA去防止过拟合不是一种好的方法,要使用正则化。因为PCA不使用y标签,可能会丢失一些有价值的信息。
三、异常检测
(一)算法
-
选择一些可以帮助我们指出异常的特征量。(即异常时它们有较大的变化)
-
拟合参数
μ j = 1 m ∑ i = 1 m x j i σ j 2 = 1 m ∑ i = 1 m ( x j i − μ j ) 2 \mu_j=\frac{1}{m}\sum_{i=1}^mx_j^i\\ \sigma^2_j=\frac{1}{m}\sum_{i=1}^m(x^i_j-\mu_j)^2 μj=m1i=1∑mxjiσj2=m1i=1∑m(xji−μj)2 -
计算概率
p ( x ) = ∏ j = 1 n p ( x j ) , x j 服 从 正 态 分 布 p(x)=\prod_{j=1}^np(x_j),x_j服从正态分布 p(x)=j=1∏np(xj),xj服从正态分布 -
比较 p(x) 与某一值 ε 的大小,判断是否异常
(二)算法评估
参考 六、算法评估中的 分割数据集成三类与误差分析中的两个算法评估指标
(三)异常检测与监督学习
- 正常样本很多而异常样本很少时,用异常检测算法
- 正常样本和异常样本都很多时,用监督学习算法
(四)多元高斯分布
多个特征取某些值概率的乘积可能会大于上面的 ε 值,使得判定为正常。但实际上某一个特征取的某一值后,其他特征取某些值的概率会很小,若恰好取到了,应该判定为异常,而按照概率乘积相乘可能会是正常。实质上是具有相关性的多元变量的高斯分布。因此计算概率也需使用多元高斯分布的概率模型。
九、推荐系统
一、基于内容的推荐算法
变量已知,有描述内容的特征量与相对应的值,使用这些内容特征量来预测。(预测思想和方法与上面监督学习的一致)
二、协同过滤
已知参数 θ 而未知特征是什么与它们的值,原本是根据特征求 θ ,现在根据 θ 求特征,求解思路一样,算法公式类似,只需根据求解对象做相应变化即可。
得到特征 X 之后,可以以此得到更好的 θ ,然后一直迭代,得到更好的值,这就是协同的思想。
实际上,不用一直迭代求最优值,可以将根据特征求 θ 的代价函数与根据 θ 求特征的代价函数相加得到一个综合的代价函数,对它整体最小化,求解出相应的值。
三、推荐
在上面的问题解决后,衡量两个东西的相似度便可向用户推荐其喜好的。衡量相似度的方法是比较特征值的相似度。
四、均值归一化
将 θ ,X,Y,都进行均值归一化的预处理,有时会让算法运行得更好一些。因为均值归一化能够处理空白值。
十、处理大数据集的算法
一、随机梯度下降
以线性回归为例:
c o s t ( θ , ( x i , y i ) ) = 1 2 ( h θ ( x i ) − y i ) 2 J t r a i n ( θ ) = 1 m ∑ i = 1 m c o s t ( θ , ( x i , y i ) ) cost(\theta,(x^i,y^i))=\frac{1}{2}(h_\theta(x^i)-y^i)^2\\ J_{train}(\theta)=\frac{1}{m}\sum_{i=1}^mcost(\theta,(x^i,y^i)) cost(θ,(xi,yi))=21(hθ(xi)−yi)2Jtrain(θ)=m1i=1∑mcost(θ,(xi,yi))
-
随机打乱数据
-
Repeat {
for i =1 to m {
θ j = θ j − α ( h θ ( x i ) − y i ) x j i \theta_j=\theta_j-\alpha(h_\theta(x^i)-y^i)x_j^i θj=θj−α(hθ(xi)−yi)xji
(for every j =0 to n) }
}
与上文中的梯度下降(批量梯度下降)比较可以看出,前者是遍历样本,每一个样本就更新一次参数;而后者在一次的参数更新中就要对所有的偏导项进行求和。因此在大数据集中随机梯度下降算法速度更快。
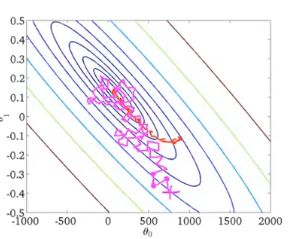
洋红色表示随机梯度下降,橙红色表示批量梯度下降:
对其收敛性的检验,可取每1000个(数量可调整)样本的cost函数均值,做出其图像。
二、Mini-batch梯度下降
b=Mini-batch size,通常可取2-100
假设b=10,m=1000
Repeat {
for i =1,11,21,…,991 {
θ j = θ j − α 10 ∑ i i + 9 ( h θ ( x i ) − y i ) x j i \theta_j=\theta_j-\frac{\alpha}{10} \sum_{i}^{i+9} (h_\theta(x^i)-y^i)x^i_j θj=θj−10αi∑i+9(hθ(xi)−yi)xji
(for every j =0 to n)
}
}
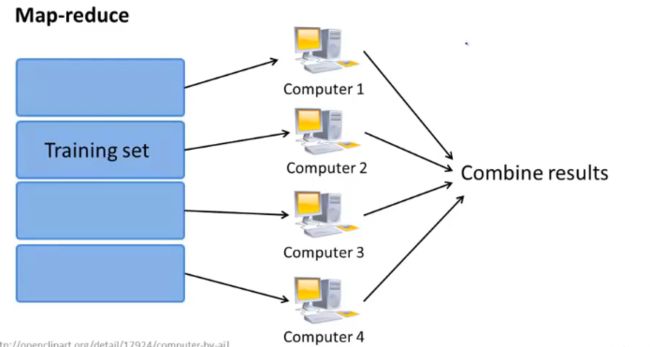
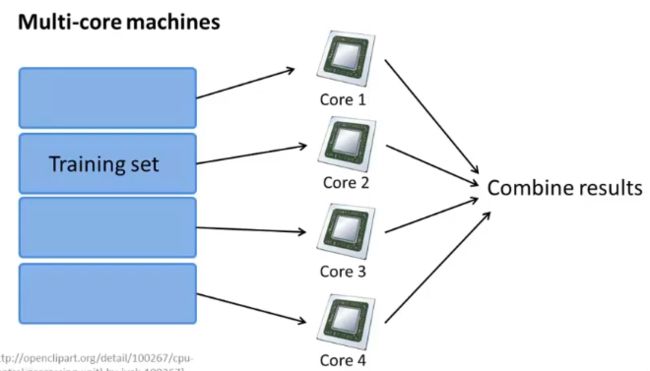
三、 MapReduce
前提:学习算法可以表示为对训练集的求和