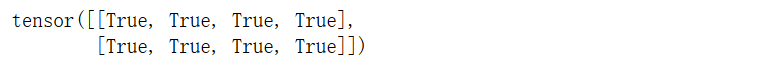Pytorch学习笔记之一

概述

前段时间分享了一些tensorflow2.0入门的笔记，其实在学术界，pytorch的热门程度是高于tensorflow2.0的。不过这些深度学习的框架多是大同小异，所以这里我也更一更torch有关的入门笔记。与tensorflow入门笔记不同，我想按模块来写torch的入门笔记。之前也大概介绍了一下torch的数据加载方式，今天主要讲torch的模型构建。
其实现有的深度学习开源框架基本都是有自动梯度求导的机制，因为自动梯度求导是神经网络能够训练的最重要的一个环节。但是autograd其实抽象程度比较低，用它来实现深度学习模型必然会使用大量的代码。在Pytorch中，torch.nn就提供了神经网络模型的构建模块，这样可以极大减轻构建模型的负担。我们只需要继承nn.Model这个父类，构建自己想要的模型就可以了。

全连接层构建

全连接层是最容易被理解的神经网络层，构建起来也非常简单，所以我们首先构建一个全连接层。

import torch as t
from torch import nn
class Linear(nn.Module): # 继承nn.Module
    def __init__(self, in_features, out_features):
        super(Linear, self).__init__() # 等价于nn.Module.__init__(self)
        self.w = nn.Parameter(t.randn(in_features, out_features))
        self.b = nn.Parameter(t.randn(out_features))
    
    def forward(self, x):
        x = x.mm(self.w) # x.@(self.w)
        return x + self.b.expand_as(x)
layer = Linear(4,3)
input = t.randn(2,4)
output = layer(input)
output

我们继承了nn.Model这个类后，全连接层的类名是Linear，需要使用__init__()函数来初始化一些参数，是输入和输出的神经元数，使用super函数拿到nn.Model的初始化。然后定义了w,b两个参数。Linear类有一个forward方法，执行的就是一个线性变化的操作。最后实例化这个类，传入参数，输入4个神经元，输出3个神经元。输入的是随机初始化的24的矩阵，最后输出。这样一个线性模型就构建成功了。最终的输出应该就是个23的矩阵。我们可以看一下参数情况：

for name, parameter in layer.named_parameters():
    print(name, parameter) # w and b 

这里有个线性代数的变换，两个矩阵相乘，如24的矩阵与43的矩阵相乘，结果就是2*3的矩阵。
注意事项：

• 在构造函数__init__中必须自己定义可学习的参数，并封装成Parameter，如在本例中我们把w和b封装成parameter。parameter是一种特殊的Tensor，但其默认需要求导（requires_grad = True）。
• forward函数实现前向传播过程，其输入可以是一个或多个tensor。
• 无需写反向传播函数，nn.Module能够利用autograd自动实现反向传播，这点比Function简单许多。
• 使用时，直观上可将layer看成数学概念中的函数，调用layer(input)即可得到input对应的结果。它等价于layers.call(input)，在__call__函数中，主要调用的是 layer.forward(x)，另外还对钩子做了一些处理。所以在实际使用中应尽量使用layer(x)而不是使用layer.forward(x)，
• Module中的可学习参数可以通过named_parameters()或者parameters()返回迭代器，前者会给每个parameter都附上名字，使其更具有辨识度。

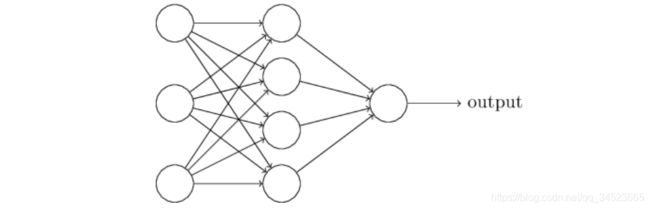
多层感知机

直接来看代码。跟上面的全连接层大同小异。

class Perceptron(nn.Module):
    def __init__(self, in_features, hidden_features, out_features):
        nn.Module.__init__(self)
        self.layer1 = Linear(in_features, hidden_features) # 此处的Linear是前面自定义的全连接层
        self.layer2 = Linear(hidden_features, out_features)
    def forward(self,x):
        x = self.layer1(x)
        x = t.sigmoid(x)
        return self.layer2(x)
perceptron = Perceptron(3,4,1)
for name, param in perceptron.named_parameters():
    print(name, param.size())

这里我们传入多了一个变量，有输入输出的神经元，还有中间隐层的神经元。全连接层调用了上面的Linear类。然后我们使用forward方法，通过两个函数来构建层与层之间的关系。
参数情况：
注意事项

• 对于类似self.param_name = nn.Parameter(t.randn(3, 4))，命名为param_name
• 对于子Module中的parameter，会其名字之前加上当前Module的名字。如对于self.sub_module = SubModel()，SubModel中有个parameter的名字叫做param_name，那么二者拼接而成的parameter name 就是sub_module.param_name。

常用神经网络层

图像相关

图像相关层主要包括卷积层（Conv）、池化层（Pool）等，这些层在实际使用中可分为一维(1D)、二维(2D)、三维（3D），池化方式又分为平均池化（AvgPool）、最大值池化（MaxPool）、自适应池化（AdaptiveAvgPool）等。而卷积层除了常用的前向卷积之外，还有逆卷积（TransposeConv）。下面举例说明一些基础的使用。
我们先找一个图片，就用经典的lena，把图片先处理成张量数据。

from PIL import Image
from torchvision.transforms import ToTensor, ToPILImage
to_tensor = ToTensor() # img -> tensor
to_pil = ToPILImage()
lena = Image.open('imgs/lena.png')
lena

# 输入是一个batch，batch_size＝1
input = to_tensor(lena).unsqueeze(0) 

# 锐化卷积核
kernel = t.ones(3, 3)/-9.
kernel[1][1] = 1
conv = nn.Conv2d(1, 1, (3, 3), 1, bias=False)
conv.weight.data = kernel.view(1, 1, 3, 3)

out = conv(input)
to_pil(out.data.squeeze(0))

池化：

pool = nn.AvgPool2d(2,2)
list(pool.parameters())
out = pool(input)
to_pil(out.data.squeeze(0))

除了卷积跟池化层，常用的还有BatchNorm，Dropout层等。
BatchNorm层：

# 4 channel，初始化标准差为4，均值为0
bn = nn.BatchNorm1d(4)
bn.weight.data = t.ones(4) * 4
bn.bias.data = t.zeros(4)

bn_out = bn(h)
# 注意输出的均值和方差
# 方差是标准差的平方，计算无偏方差分母会减1
# 使用unbiased=False 分母不减1
bn_out.mean(0), bn_out.var(0, unbiased=False)

dropout使用：

# 每个元素以0.5的概率舍弃
dropout = nn.Dropout(0.5)
o = dropout(bn_out)
o # 有一半左右的数变为0

激活函数

常见的激活函数也是可以使用nn直接调用。

relu = nn.ReLU(inplace=True)
input = t.randn(2, 3)
print(input)
output = relu(input)
print(output) # 小于0的都被截断为0
# 等价于input.clamp(min=0)

这里的inplace为True时，模型会把输出直接覆盖输入。但是一般不要使用inplace操作，避免不必要的麻烦。

与tensorflow2类似，Pytorch中也是可以使用Sequential这种些话构建模型：

# Sequential的三种写法
net1 = nn.Sequential()
net1.add_module('conv', nn.Conv2d(3, 3, 3))
net1.add_module('batchnorm', nn.BatchNorm2d(3))
net1.add_module('activation_layer', nn.ReLU())

net2 = nn.Sequential(
        nn.Conv2d(3, 3, 3),
        nn.BatchNorm2d(3),
        nn.ReLU()
        )

from collections import OrderedDict
net3= nn.Sequential(OrderedDict([
          ('conv1', nn.Conv2d(3, 3, 3)),
          ('bn1', nn.BatchNorm2d(3)),
          ('relu1', nn.ReLU())
        ]))
print('net1:', net1)
print('net2:', net2)
print('net3:', net3)

循环神经网络

t.manual_seed(1000)
# 输入：batch_size=3，序列长度都为2，序列中每个元素占4维
input = t.randn(2, 3, 4)
# lstm输入向量4维，隐藏元3，1层
lstm = nn.LSTM(4, 3, 1)
# 初始状态：1层，batch_size=3，3个隐藏元
h0 = t.randn(1, 3, 3)
c0 = t.randn(1, 3, 3)
out, hn = lstm(input, (h0, c0))
out

我们输入维度是 234，LSTM的输入为4维，3个单元，只有一层。这里的batch_size为3，那么输入之后的维度应该是233这样的格式。

t.manual_seed(1000)
input = t.randn(2, 3, 4)
# 一个LSTMCell对应的层数只能是一层
lstm = nn.LSTMCell(4, 3)
hx = t.randn(3, 3)
cx = t.randn(3, 3)
out = []
for i_ in input:
    hx, cx=lstm(i_, (hx, cx))
    out.append(hx)
t.stack(out)

自然语言处理

LSTM在自然语言处理中非常常见。此外，词向量也是非常重要的一环。Pytorch也提供了Embedding层，用于将文本转换成向量，便于模型处理。`

# 有4个词，每个词用5维的向量表示
embedding = nn.Embedding(4, 5)
# 可以用预训练好的词向量初始化embedding
embedding.weight.data = t.arange(0,20).view(4,5)
input = t.arange(3, 0, -1).long()
output = embedding(input)
output

这里我们没有预训练，所以使用生成了一个45的向量表，将输入的三个字符嵌入成35的形式。

损失函数

# batch_size=3，计算对应每个类别的分数（只有两个类别）
score = t.randn(3, 2)
# 三个样本分别属于1，0，1类，label必须是LongTensor
label = t.Tensor([1, 0, 1]).long()

# loss与普通的layer无差异
criterion = nn.CrossEntropyLoss()
loss = criterion(score, label)
loss

优化器

我们首先定义一个网络：

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.features = nn.Sequential(
                    nn.Conv2d(3, 6, 5),
                    nn.ReLU(),
                    nn.MaxPool2d(2,2),
                    nn.Conv2d(6, 16, 5),
                    nn.ReLU(),
                    nn.MaxPool2d(2,2)
        )
        self.classifier = nn.Sequential(
            nn.Linear(16 * 5 * 5, 120),
            nn.ReLU(),
            nn.Linear(120, 84),
            nn.ReLU(),
            nn.Linear(84, 10)
        )

    def forward(self, x):
        x = self.features(x)
        x = x.view(-1, 16 * 5 * 5)
        x = self.classifier(x)
        return x

net = Net()

所有的优化方法都是继承基类optim.Optimizer。

from torch import  optim
optimizer = optim.SGD(params=net.parameters(), lr=1)
optimizer.zero_grad() # 梯度清零，等价于net.zero_grad()

input = t.randn(1, 3, 32, 32)
output = net(input)
output.backward(output) # fake backward

optimizer.step() # 执行优化

# 为不同子网络设置不同的学习率，在finetune中经常用到
# 如果对某个参数不指定学习率，就使用最外层的默认学习率
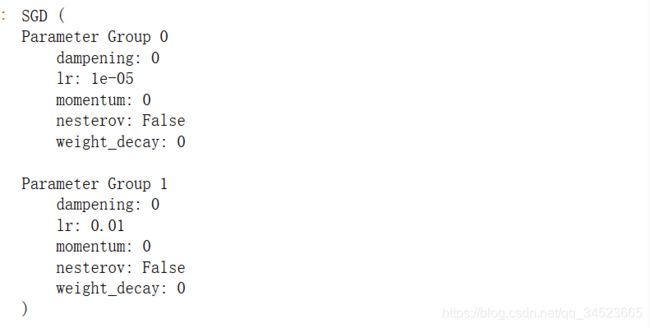
optimizer =optim.SGD([
                {'params': net.features.parameters()}, # 学习率为1e-5
                {'params': net.classifier.parameters(), 'lr': 1e-2}
            ], lr=1e-5)
optimizer

special_layers = nn.ModuleList([net.classifier[0], net.classifier[3]])
special_layers_params = list(map(id, special_layers.parameters()))
base_params = filter(lambda p: id(p) not in special_layers_params,
                     net.parameters())

optimizer = t.optim.SGD([
            {'params': base_params},
            {'params': special_layers.parameters(), 'lr': 0.01}
        ], lr=0.001 )
optimizer

对于如何调整学习率，主要有两种做法。一种是修改optimizer.param_groups中对应的学习率，另一种是更简单也是较为推荐的做法——新建优化器，由于optimizer十分轻量级，构建开销很小，故而可以构建新的optimizer。但是后者对于使用动量的优化器（如Adam），会丢失动量等状态信息，可能会造成损失函数的收敛出现震荡等情况。

# 方法1: 调整学习率，新建一个optimizer
old_lr = 0.1
optimizer1 =optim.SGD([
                {'params': net.features.parameters()},
                {'params': net.classifier.parameters(), 'lr': old_lr*0.1}
            ], lr=1e-5)
optimizer1

# 方法2: 调整学习率, 手动decay, 保存动量
for param_group in optimizer.param_groups:
    param_group['lr'] *= 0.1 # 学习率为之前的0.1倍
optimizer

nn.functional模块

神经网络中的多数函数都会在nn.functional中有对应的。nn.Model实现的是layers的一个特殊的类，可以自动提取可学习的参数。functional是纯函数。
我们使用两种方法都定义模型：

input = t.randn(2, 3)
model = nn.Linear(3, 4)
output1 = model(input)
output2 = nn.functional.linear(input, model.weight, model.bias)
output1 == output2

b = nn.functional.relu(input)
b2 = nn.ReLU()(input)
b == b2

我们看到这种情况下二者是相同的。那我们怎么选择两种方式呢？如果像激活层，池化层这种没有可学习的参数，就可以用functional，其他尽量使用model类。

from torch.nn import functional as F
class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(3, 6, 5)
        self.conv2 = nn.Conv2d(6, 16, 5)
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        x = F.pool(F.relu(self.conv1(x)), 2)
        x = F.pool(F.relu(self.conv2(x)), 2)
        x = x.view(-1, 16 * 5 * 5)
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

上面可以看出来，自己定义一些层的参数比较麻烦：

class MyLinear(nn.Module):
    def __init__(self):
        super(MyLinear, self).__init__()
        self.weight = nn.Parameter(t.randn(3, 4))
        self.bias = nn.Parameter(t.zeros(3))
    def forward(self):
        return F.linear(input, weight, bias)

初始化策略

如果不继承Model，当我们使用parameter时，初始化策略就显得很重要，好的初始化能够加快模型收敛，不好的初始化可能会导致模型瘫痪。

# 利用nn.init初始化
from torch.nn import init
linear = nn.Linear(3, 4)

t.manual_seed(1)
# 等价于 linear.weight.data.normal_(0, std)
init.xavier_normal_(linear.weight)

# 直接初始化
import math
t.manual_seed(1)

# xavier初始化的计算公式
std = math.sqrt(2)/math.sqrt(7.)
linear.weight.data.normal_(0,std)

# 对模型的所有参数进行初始化
for name, params in net.named_parameters():
    if name.find('linear') != -1:
        # init linear
        params[0] # weight
        params[1] # bias
    elif name.find('conv') != -1:
        pass
    elif name.find('norm') != -1:
        pass