一步一步讲解和实现ASR中常用的语音特征——FBank和MFCC的提取,包括算法原理、代码和可视化等。
完整Jupyter Notebook链接:https://github.com/Magic-Bubble/SpeechProcessForMachineLearning/blob/master/speech_process.ipynb
文章目录
-
- 语音信号的产生
- 准备工作
-
- 预加重(Pre-Emphasis)
- 分帧(Framing)
- 加窗(Window)
- 快速傅里叶变换(FFT)
- FBank特征(Filter Banks)
- MFCC特征(Mel-frequency Cepstral Coefficients)
- FBank与MFCC比较
- 其他特征
- 标准化
- 总结
- 传送门
语音信号的产生
语音通常是指人说话的声音。从生物学的角度来看,是气流通过声带、咽喉、口腔、鼻腔等发出声音;从信号的角度来看,不同位置的震动频率不一样,最后的信号是由基频和一些谐波构成。

之后被设备接收后(比如麦克风),会通过A/D转换,将模拟信号转换为数字信号,一般会有采样、量化和编码三个步骤,采样率要遵循奈奎斯特采样定律:
f
s
>
=
2
f
fs >= 2f
fs>=2f,比如电话语音的频率一般在300Hz~3400Hz,所以采用8kHz的采样率足矣。
下面采用一个30s左右的16比特PCM编码后的语音wav为例。
准备工作
1. 导包
import numpy as np
from scipy.io import wavfile
from scipy.fftpack import dct
import warnings
warnings.filterwarnings('ignore')
import matplotlib.pyplot as plt
%matplotlib inline
2. 绘图工具
def plot_time(signal, sample_rate):
time = np.arange(0, len(signal)) * (1.0 / sample_rate)
plt.figure(figsize=(20, 5))
plt.plot(time, signal)
plt.xlabel('Time(s)')
plt.ylabel('Amplitude')
plt.grid()
def plot_freq(signal, sample_rate, fft_size=512):
xf = np.fft.rfft(signal, fft_size) / fft_size
freqs = np.linspace(0, sample_rate/2, fft_size/2 + 1)
xfp = 20 * np.log10(np.clip(np.abs(xf), 1e-20, 1e100))
plt.figure(figsize=(20, 5))
plt.plot(freqs, xfp)
plt.xlabel('Freq(hz)')
plt.ylabel('dB')
plt.grid()
def plot_spectrogram(spec, note):
fig = plt.figure(figsize=(20, 5))
heatmap = plt.pcolor(spec)
fig.colorbar(mappable=heatmap)
plt.xlabel('Time(s)')
plt.ylabel(note)
plt.tight_layout()
3. 数据准备
sample_rate, signal = wavfile.read('./resources/OSR_us_000_0010_8k.wav')
signal = signal[0: int(3.5 * sample_rate)]
print('sample rate:', sample_rate, ', frame length:', len(signal))
sample rate: 8000 , frame length: 28000
plot_time(signal, sample_rate)
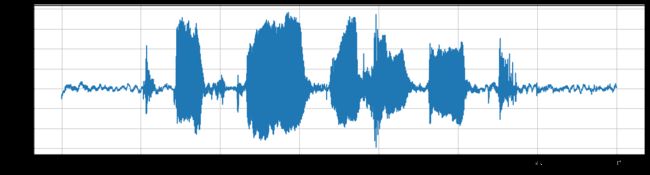
plot_freq(signal, sample_rate)

预加重(Pre-Emphasis)
预加重一般是数字语音信号处理的第一步。语音信号往往会有频谱倾斜(Spectral Tilt)现象,即高频部分的幅度会比低频部分的小,预加重在这里就是起到一个平衡频谱的作用,增大高频部分的幅度。它使用如下的一阶滤波器来实现:
y
(
t
)
=
x
(
t
)
−
α
x
(
t
−
1
)
,
0.95
<
α
<
0.99
y(t) = x(t) - \alpha x(t-1), \ \ \ \ 0.95 < \alpha < 0.99
y(t)=x(t)−αx(t−1), 0.95<α<0.99
笔者对这个公式的理解是:信号频率的高低主要是由信号电平变化的速度所决定,对信号做一阶差分时,高频部分(变化快的地方)差分值大,低频部分(变化慢的地方)差分值小,达到平衡频谱的作用。
pre_emphasis = 0.97
emphasized_signal = np.append(signal[0], signal[1:] - pre_emphasis * signal[:-1])
plot_time(emphasized_signal, sample_rate)
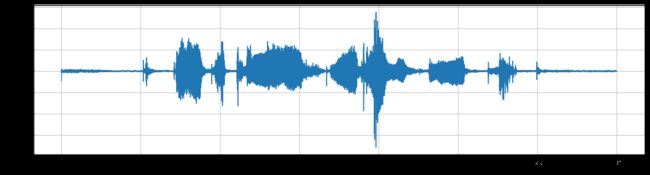
plot_freq(emphasized_signal, sample_rate)

从下面这个图来看,确实起到了平衡频谱的作用。
分帧(Framing)
在预加重之后,需要将信号分成短时帧。做这一步的原因是:信号中的频率会随时间变化(不稳定的),一些信号处理算法(比如傅里叶变换)通常希望信号是稳定,也就是说对整个信号进行处理是没有意义的,因为信号的频率轮廓会随着时间的推移而丢失。为了避免这种情况,需要对信号进行分帧处理,认为每一帧之内的信号是短时不变的。一般设置帧长取20ms~40ms,相邻帧之间50%(+/-10%)的覆盖。对于ASR而言,通常取帧长为25ms,覆盖为10ms。
frame_size, frame_stride = 0.025, 0.01
frame_length, frame_step = int(round(frame_size * sample_rate)), int(round(frame_stride * sample_rate))
signal_length = len(emphasized_signal)
num_frames = int(np.ceil(np.abs(signal_length - frame_length) / frame_step)) + 1
pad_signal_length = (num_frames - 1) * frame_step + frame_length
z = np.zeros((pad_signal_length - signal_length))
pad_signal = np.append(emphasized_signal, z)
indices = np.arange(0, frame_length).reshape(1, -1) + np.arange(0, num_frames * frame_step, frame_step).reshape(-1, 1)
frames = pad_signal[indices]
print(frames.shape)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
(349, 200)
加窗(Window)
在分帧之后,通常需要对每帧的信号进行加窗处理。目的是让帧两端平滑地衰减,这样可以降低后续傅里叶变换后旁瓣的强度,取得更高质量的频谱。常用的窗有:矩形窗、汉明(Hamming)窗、汉宁窗(Hanning),以汉明窗为例,其窗函数为:
w
(
n
)
=
0.54
−
0.46
c
o
s
(
2
π
n
N
−
1
)
w(n) = 0.54 - 0.46 cos(\frac{2\pi n}{N-1})
w(n)=0.54−0.46cos(N−12πn)
这里的
0
<
=
n
<
=
N
−
1
0<=n<=N-1
0<=n<=N−1,
N
N
N是窗的宽度。
hamming = np.hamming(frame_length)
plt.figure(figsize=(20, 5))
plt.plot(hamming)
plt.grid()
plt.xlim(0, 200)
plt.ylim(0, 1)
plt.xlabel('Samples')
plt.ylabel('Amplitude')

frames *= hamming
plot_time(frames[1], sample_rate)

plot_freq(frames[1], sample_rate)
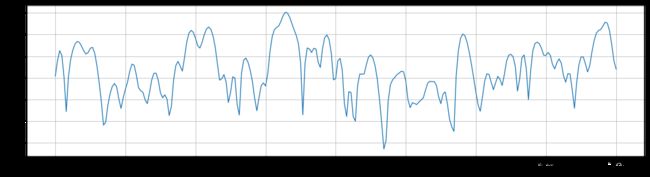
快速傅里叶变换(FFT)
对于每一帧的加窗信号,进行N点FFT变换,也称短时傅里叶变换(STFT),N通常取256或512,然后用如下的公式计算能量谱:
P
=
∣
F
F
T
(
x
i
)
∣
2
N
P = \frac{|FFT(x_i)|^2}{N}
P=N∣FFT(xi)∣2
NFFT = 512
mag_frames = np.absolute(np.fft.rfft(frames, NFFT))
pow_frames = ((1.0 / NFFT) * (mag_frames ** 2))
print(pow_frames.shape)
(349, 257)
plt.figure(figsize=(20, 5))
plt.plot(pow_frames[1])
plt.grid()

FBank特征(Filter Banks)
经过上面的步骤之后,在能量谱上应用Mel滤波器组,就能提取到FBank特征。
在介绍Mel滤波器组之前,先介绍一下Mel刻度,这是一个能模拟人耳接收声音规律的刻度,人耳在接收声音时呈现非线性状态,对高频的更不敏感,因此Mel刻度在低频区分辨度较高,在高频区分辨度较低,与频率之间的换算关系为:
m
=
2595
l
o
g
10
(
1
+
f
700
)
m = 2595 log_{10} (1 + \frac{f}{700})
m=2595log10(1+700f)
f
=
700
(
1
0
m
/
2595
−
1
)
f = 700(10^{m/2595} - 1)
f=700(10m/2595−1)
Mel滤波器组就是一系列的三角形滤波器,通常有40个或80个,在中心频率点响应值为1,在两边的滤波器中心点衰减到0,如下图:

具体公式可以写为:

最后在能量谱上应用Mel滤波器组,其公式为:
Y
t
(
m
)
=
∑
k
=
1
N
H
m
(
k
)
∣
X
t
(
k
)
∣
2
Y_t(m) = \sum_{k=1}^{N} H_m(k)|X_t(k)|^2
Yt(m)=k=1∑NHm(k)∣Xt(k)∣2
其中,k表示FFT变换后的编号,m表示mel滤波器的编号。
low_freq_mel = 0
high_freq_mel = 2595 * np.log10(1 + (sample_rate / 2) / 700)
print(low_freq_mel, high_freq_mel)
0 2146.06452750619
nfilt = 40
mel_points = np.linspace(low_freq_mel, high_freq_mel, nfilt + 2)
hz_points = 700 * (10 ** (mel_points / 2595) - 1)
fbank = np.zeros((nfilt, int(NFFT / 2 + 1)))
bin = (hz_points / (sample_rate / 2)) * (NFFT / 2)
for i in range(1, nfilt + 1):
left = int(bin[i-1])
center = int(bin[i])
right = int(bin[i+1])
for j in range(left, center):
fbank[i-1, j+1] = (j + 1 - bin[i-1]) / (bin[i] - bin[i-1])
for j in range(center, right):
fbank[i-1, j+1] = (bin[i+1] - (j + 1)) / (bin[i+1] - bin[i])
print(fbank)
[[0. 0.46952675 0.93905351 … 0. 0. 0. ]
[0. 0. 0. … 0. 0. 0. ]
[0. 0. 0. … 0. 0. 0. ]
…
[0. 0. 0. … 0. 0. 0. ]
[0. 0. 0. … 0. 0. 0. ]
[0. 0. 0. … 0.14650797 0.07325398 0. ]]
filter_banks = np.dot(pow_frames, fbank.T)
filter_banks = np.where(filter_banks == 0, np.finfo(float).eps, filter_banks)
filter_banks = 20 * np.log10(filter_banks)
print(filter_banks.shape)
(349, 40)
plot_spectrogram(filter_banks.T, 'Filter Banks')
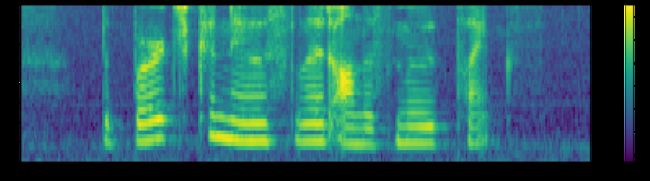
PS:“log mel-filter bank outputs”和“FBANK features”说的是同一个东西。
MFCC特征(Mel-frequency Cepstral Coefficients)
前面提取到的FBank特征,往往是高度相关的。因此可以继续用DCT变换,将这些相关的滤波器组系数进行压缩。对于ASR来说,通常取2~13维,扔掉的信息里面包含滤波器组系数快速变化部分,这些细节信息在ASR任务上可能没有帮助。
DCT变换其实是逆傅里叶变换的等价替代:
y
t
(
n
)
=
∑
m
=
0
M
−
1
l
o
g
(
Y
t
(
m
)
)
c
o
s
(
n
(
m
+
0.5
)
π
M
)
,
n
=
0
,
.
.
.
,
J
y_t(n) = \sum_{m=0}^{M-1}log(Y_t(m))cos(n(m + 0.5) \frac{\pi}{M}), \ \ \ \ \ n = 0, ..., J
yt(n)=m=0∑M−1log(Yt(m))cos(n(m+0.5)Mπ), n=0,...,J
所以MFCC名字里面有倒谱(Cepstral)。
num_ceps = 12
mfcc = dct(filter_banks, type=2, axis=1, norm='ortho')[:, 1:(num_ceps+1)]
print(mfcc.shape)
(349, 12)
plot_spectrogram(mfcc.T, 'MFCC Coefficients')
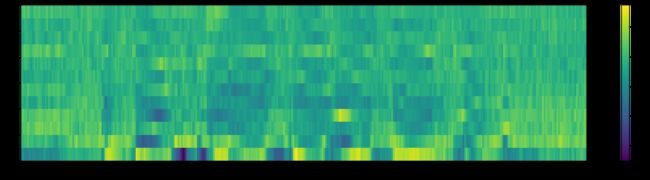
一般对于ASR来说,对MFCC进行一个正弦提升(sinusoidal liftering)操作,可以提升在噪声信号中最后的识别率:
M
F
C
C
i
′
=
w
i
M
F
C
C
i
MFCC'_i = w_i MFCC_i
MFCCi′=wiMFCCi
w
i
=
D
2
s
i
n
(
π
∗
i
D
)
w_i = \frac{D}{2} sin(\frac{\pi * i}{D})
wi=2Dsin(Dπ∗i)
从公式看,猜测原因可能是对频谱做一个平滑,如果
D
D
D取值较大时,会加重高频部分,使得噪声被弱化?
cep_lifter = 23
(nframes, ncoeff) = mfcc.shape
n = np.arange(ncoeff)
lift = 1 + (cep_lifter / 2) * np.sin(np.pi * n / cep_lifter)
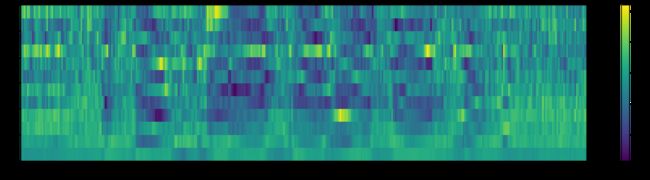
mfcc *= lift
plot_spectrogram(mfcc.T, 'MFCC Coefficients')
FBank与MFCC比较
FBank特征的提取更多的是希望符合声音信号的本质,拟合人耳接收的特性。而MFCC特征多的那一步则是受限于一些机器学习算法。很早之前MFCC特征和GMMs-HMMs方法结合是ASR的主流。而当一些深度学习方法出来之后,MFCC则不一定是最优选择,因为神经网络对高度相关的信息不敏感,而且DCT变换是线性的,会丢失语音信号中原本的一些非线性成分。
还有一些说法是在质疑傅里叶变换的使用,因为傅里叶变换也是线性的。因此也有很多方法,设计模型直接从原始的音频信号中提取特征,但这种方法会增加模型的复杂度,而且本身傅里叶变换不太容易拟合。同时傅里叶变换是在短时上应用的,可以建设信号在这个短的时间内是静止的,因此傅里叶变换的线性也不会造成很严重的问题。
结论就是:在模型对高相关的信号不敏感时(比如神经网络),可以用FBank特征;在模型对高相关的信号敏感时(比如GMMs-HMMs),需要用MFCC特征。从目前的趋势来看,因为神经网络的逐步发展,FBank特征越来越流行。
其他特征
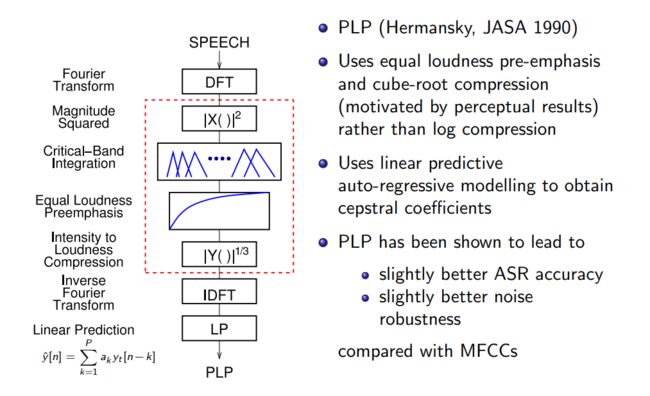
- PLP(Perceptual Linear Prediction)
另外一种特征,与MFCC相比有一些优势,具体提取方式见下图:
- 动态特征
加入表现帧之间变化的特征,用如下公式:
d
(
t
)
=
c
(
t
+
1
)
−
c
(
t
−
1
)
2
d(t) = \frac{c(t+1) - c(t-1)}{2}
d(t)=2c(t+1)−c(t−1)
一般在ASR中使用的特征(用于GMM相关的系统),是39维的;包括(12维MFCC+1维能量) + delta + delta^2
具体提取过程见下图:

标准化
其目的是希望减少训练集与测试集之间的不匹配。有三种操作:
- 去均值 (CMN)
为了均衡频谱,提升信噪比,可以做一个去均值的操作
filter_banks -= (np.mean(filter_banks, axis=0) + 1e-8)
plot_spectrogram(filter_banks.T, 'Filter Banks')

mfcc -= (np.mean(mfcc, axis=0) + 1e-8)
plot_spectrogram(mfcc.T, 'MFCC Coefficients')

- 方差归一(CVN)
除以标准差,从而使得方差为1
- 标准化(CMVN)
y
t
(
j
)
=
y
t
(
j
)
−
μ
(
y
(
j
)
)
σ
(
y
(
j
)
)
y_t(j) = \frac{y_t(j) - \mu (y(j))}{\sigma (y(j))}
yt(j)=σ(y(j))yt(j)−μ(y(j))
PS:这些操作,还可以针对speaker/channel做;在实时情景下,可以计算moving average。
总结
最后引用文末slide里面的一个总结:

传送门
Speech Processing for Machine Learning: Filter banks, Mel-Frequency Cepstral Coefficients (MFCCs) and What’s In-Between 一个很优质,讲的很清楚的英文博客
Speech Signal Analysis 英国爱丁堡大学一门ASR课程的讲义
python_speech_features 一个很成熟的python提取这些特征的包
ASR中常用的语音特征之FBank和MFCC(原理 + Python实现) 个人博客
文章知识点与官方知识档案匹配,可进一步学习相关知识
Python入门技能树首页概览 178737 人正在系统学习中